Задания для самостоятельного решения

1.Вычислить определители.

а) 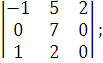б)

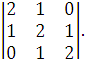
2. Вычислить ЗА + 2В, где .

3. Дана матрица 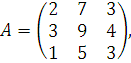найти .

4. Вычислить ранг матрицы.

б) .

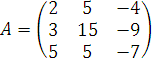1.3. Линейное (векторное) пространство

Определение. Совокупность n действительных чисел заданных в определенном порядке, называется n-мерным вектором. Числа называются координатами вектора.

Над n-мерными векторами вводятся следующие операции.

Сложение: , то

Умножение на число: если λ - действительное число и – вектор, то

Определение. Два вектора называются равными, если равны их соответствующие координаты

Среди n-мерных векторов есть вектор, нейтральный относительно операции сложения. Это вектор с нулевыми координатами. Его называют нулевым вектором и обозначают через 0:

0 = (0, 0, ..., 0).

Каждый вектор х имеет противоположный; его обозначают - х, причем

Введенные операции сложения векторов и умножение вектора на число обладают восемью свойствами:

1) х + у = у + х;

2) (x + y) + z = x + (y + z);

3) х + 0 = 0;

4) х + (-х) = 0;

5)λ(μx) = (λμ)x;

6) λ(х + у) = λх + λу;

7) (λ + μ)x = λх + μx;

8) 1 ∙ x = x.

Определение. Множество всех n-мерных векторов,для которых установлены операции сложения иумножения на число, называется n-мерным векторным(линейным) пространством .

Определение. Система n-мерных векторов называется линейно зависимой, если найдутся числ , не равные одновременно нулю, такие, что

В противном случае эта система называется линейно независимой.

Определение. Пусть Q - произвольное множество n-мерных векторов пространства . Система векторов называется базисом в Q, есливыполняются следующие условия:

1) ;

2) система линейно независима;

3) для любого вектора найдутся числа такие, что .

Определение. Формула называется разложением вектора х по базису .Коэффициенты однозначно определяются вектором х и называются координатами этого вектора в базисе В.

Справедливы следующие утверждения:

1) Всякая система векторов имеет по меньшей мере один базис; при этом все базисы этой системы состоят из одинакового числа векторов, называемого рангом системы Q, и обозначаются r(Q).

2) Ранг всего пространства равен n и называется размерностью этого пространства; при этом в качестве базиса можно взять следующую систему:

,

…

.

Этот базис принято называть каноническим.

Зафиксируем произвольный базис впространстве . Тогда всякому вектору х можнопоставить во взаимно однозначное соответствие столбец его координат в этом базисе, т. е.

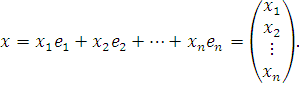
1.4. Системы линейныхалгебраических уравнений Системы n линейных алгебраических уравнений с n неизвестными

Пусть дана система n линейных алгебраических уравнений с n неизвестными вида

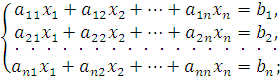
или в матричной форме, АХ = b, где 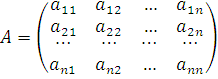- матрица системы,

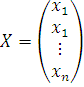- матрица-столбец неизвестных,

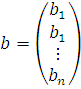- матрица-столбец свободных членов данной системы.

Правило Крамера

Если в системе , т. е. матрица А имеет обратную , то система имеет, и притом единственное, решение

или ,

где - определитель, получаемый из определителя ∆системы заменой i-гo столбца на столбец свободных членов.

Пример. Решить систему уравнений по правилу Крамера

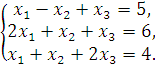
Решение:

Определитель системы

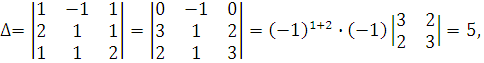
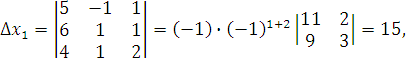
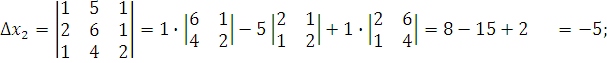
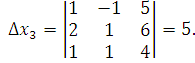
Тогда

Ответ:

Пример. Решить систему линейных алгебраических уравнений матричным способом.

Решение:

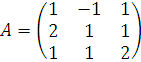- матрица системы уравнений,

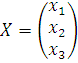- матрица-столбец неизвестных,

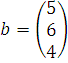- матрица-столбец свободных членов данной системы.

Так как в первом примере вычислен определитель системы и он равенdet А = 5 ≠ 0, то матрица А имеет обратную матрицу .

Вычислим

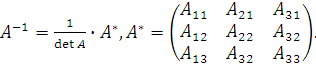
Получили присоединенную матрицу

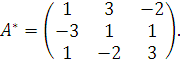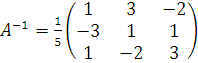Тогда ирешение системы найдем по формуле ,

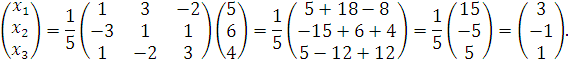
Отсюда: .

Ответ: .