Задания для самостоятельного решения

1. Даны две точки М (1; 3; 5) и К(7; 8; 9). Составить

а) канонические и б) параметрические уравненияпрямой, проходящей через данные точки М и К.

2. Составить канонические уравнения прямой, проходящей через точку параллельно:

а) вектору = (2; -3; 5);

б) прямой ; в) оси Ох; г) оси Оу; д) оси Oz.

3. Составить канонические уравнения прямой, проходящей через две данные точки: а) (1; -2; 1), (3; 1; -1); б) (3; -1; 0), (1; 0; -3); в) (0; -2; 3), (3; -2; 1); г) (1; 2; -4), (-1; 2; -4).

4. Составить канонические уравнения следующих прямых:

а) б)

в)

5. Найти координаты точки К пересечения прямой:

с плоскостью: 2х + 5у - Зz = 0.

10. Вычислить расстояние d точки Р(1; -1; -2) от прямой

.

4.4 Линии второго порядка

Кривыми второго порядка называются линии, определяемые в декартовых координатах алгебраическими уравнениями второй степени. В частности, окружность, эллипс, гипербола и парабола являются такими линиями.

Этими четырьмя линиями и случаями их вырождения, когда уравнение второй степени определяет пустое множество (мнимая кривая), точку, прямую, пару прямых, исчерпываются все линии, определяемые алгебраическими уравнениями второй степени.

Окружность

Определение. Окружностью называется множествоточек плоскости, равноудаленных от данной точки (центра).

Если R - радиус окружности, а С(а, b) - ее центр, тоуравнение окружности имеет вид

. (*)

В частности, если центр окружности совпадает сначалом координат, то уравнение окружности (*) примет вид

.

Взаимное расположение точки и окружности определяется такими условиями:

если , то точка М лежит на окружности;

если , то точка М лежит вне окружности;

если , то точка М лежит внутри окружности.

Пример. Написать уравнение окружности радиуса R = 8 с центром в точке С(2; -5).

Решение:

Подставив значения координат точки С и значение радиуса в формулу (1), получим

или .

Ответ: .

Пример. Доказать, что уравнение является уравнением окружности. Найти ее центр и радиус.

Решение:

Преобразуем левую часть данного уравнения, выделив полные квадраты относительно х и у:

, или

. Это уравнение представляет собой уравнение окружности с центром С(-4; 2) и радиусом, равным 5.

Ответ: С(-А; 2), R = 5.

Пример. Найти координаты центра и радиусокружности

Решение:

Разделив уравнение на 2 и сгруппировав члены уравнения, получим . Дополним выражения и до полных квадратов, прибавивк первому двучлену 4 и ко второму – , одновременно к правой части прибавляется сумма этих чисел:

, или

. Таким образом, координаты центра окружности а = 2, b = , а радиус окружности .

Ответ: .

Эллипс

Определение. Эллипсом называется множество точекплоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.

Каноническое уравнение эллипса в прямоугольной системе координат

Определение. Величины а и b называются соответственно большой и малой полуосями эллипса (а >b).Фокусы эллипса расположены в точках ,точки - вершины эллипса, оси координат Оx и Оу - оси симметрии, а началокоординат О(0, 0) - центр симметрии эллипса.

О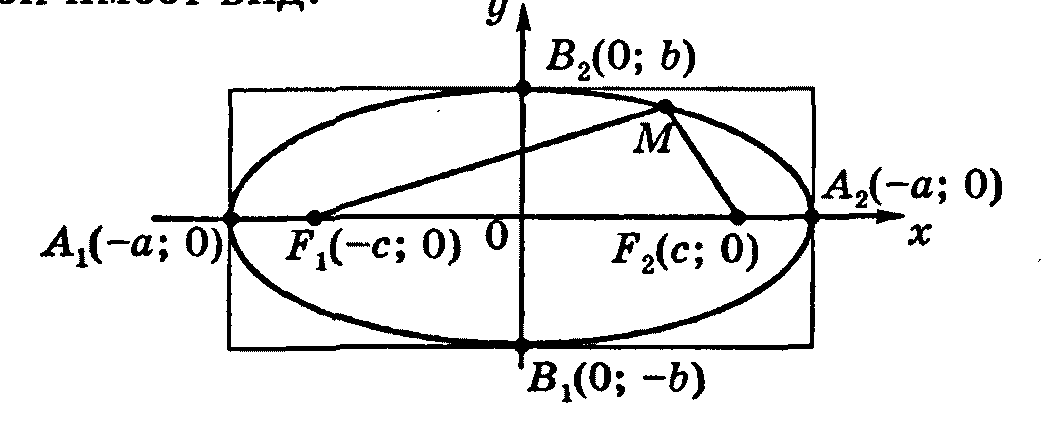 пределение. Число называется эксцентриситетом эллипса, он является мерой«сжатости» к оси Ох (при е = 0 эллипс является окружностью).

Форма кривой имеет вид:

Уравнение касательной к эллипсу в точке имеет вид:

Пример. Найти каноническое уравнение эллипса, зная его большую полуось а = 5 и эксцентриситет е = 0,6.

Решение:

По условию . Следовательно, . Но тогда квадрат малой полуоси эллипса . Таким образом, искомое каноническое уравнение эллипса имеет вид:

Ответ: .

Пример. Составить каноническое уравнение эллипса, проходящего через точку и имеющегобольшую полуось а = 4.

Решение:

Каноническое уравнение эллипса при а = 4 имеет следующий вид:

(**)

Этому уравнению должны удовлетворять координаты точки . Следовательно, . Найдя отсюда и подставив его в уравнение (**), получим искомое каноническое уравнение эллипса:

Ответ: .

Пример. Составить каноническое уравнение эллипса, проходящего через точки

Решение:

Пусть - искомое уравнение эллипса. Этому уравнению должны удовлетворять координаты точек. Следовательно,

Отсюда находим . Итак, уравнение эллипса имеет вид:

Ответ: .

Пример. Написать каноническое уравнение эллипса, проходящего через точку М(6; 0), если фокальное расстояние равно 4.

Решение: Подставим координаты точки М(6; 0) в каноническое уравнение эллипса , получим , отсюда . Найдем , где с - половина фокального расстояния эллипса. По условию с = 2. Тогда . Итак, искомым уравнением эллипса будет уравнение . Ответ: .

Пример. Доказать, что уравнение является уравнением эллипса. Найти координаты фокусов и фокальное расстояние.

Решение: Разделив обе части уравнения на 6400, получим: .Это уравнение является каноническим уравнением эллипса. Из равенства следует, что и с = 6. Фокусы эллипса будут находиться в точках . Фокальное расстояние 2с = 12.

Ответ: .

Пример. Эллипс, симметричный относительно осей координат, фокусы которого находятся на оси Ох,проходит через точку М(-4; √21) и имеет эксцентриситет . Написать уравнение эллипса.

Решение: Каноническое уравнение эллипса:

По условию: , т. е.

, или . Отсюда .Так как точка М(-4; √21) принадлежит эллипсу, то еекоординаты удовлетворяют уравнению эллипса:

. Для нахождения величины подставим вэто равенство , получим , или

Найдем .

Итак, искомое уравнение эллипса есть .

Ответ: .