Задания для самостоятельного решения

1. Точки расположены на прямой ; их абсциссы соответственно равны числам: 4, 0, 2, –2 и 6. Определить ординаты этих точек.

2. Преобразовать уравнение куравнению в отрезках.

3. Найти угол между прямой и прямой .

4. Найти уравнение прямой, проходящей через точки .

5. Даны вершины треугольника А(2; 5), В (-3; 1), С (4; -2). Найти уравнение высоты треугольника, опущенной из вершины А.

6. Найти уравнение прямой, проходящей через точкупересечения прямых и и через точку .

7. Дан треугольник ABC с вершинами в точках А(3; -5), В(2; 1), С(0; 5). Составить уравнения стороны АВ, высоты BD и медианы AM.

8. Определить угол φ между двумя прямыми:

.

9. Установить, какие из следующих пар прямыхперпендикулярны:

а) , б) ,

; ;

в) , г) ,

; ;

д) , е) ,

; .

10. Дана прямая 2x + Зу + 4 = 0. Составить уравнениепрямой, проходящей через точку :

а) параллельно данной прямой;

б) перпендикулярно к данной прямой.

11. Доказать, что в следующих случаях две данные прямые параллельны:

а) , б) 2х - 4у + 3 = 0,

6х + 10у + 7 = 0; ;

в) 2х – 1 = 0, г) у + 3 = 0,

x + 3 = 0; 5у – 7 = 0.

4.2 Плоскость

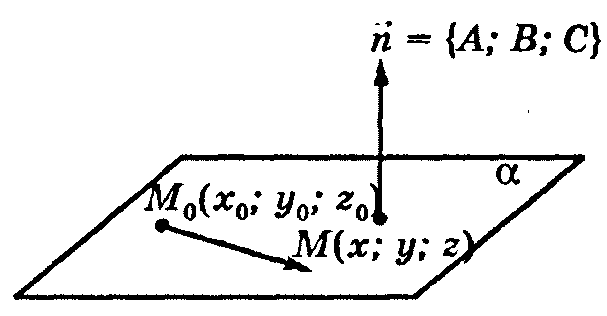
– уравнение плоскости, проходящей через точку перпендикулярно нормальному вектору = =(А; В; С).

2).Ах + By + Cz + D = 0 – общее уравнение плоскости, = (А; В; С)- нормальный вектор этой плоскости.

3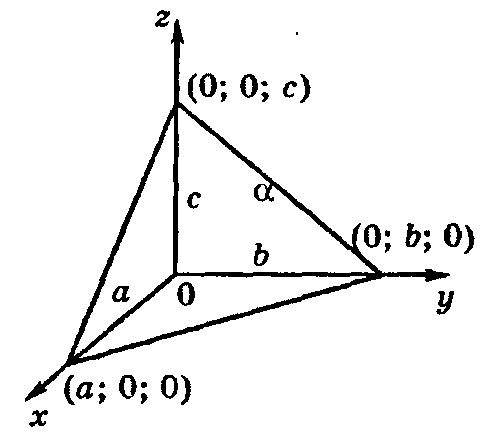 ). – уравнение плоскости в отрезках, где а, b,с - величины направленных отрезков, отсекаемых плоскостьюа на координатных осях Ох, Оу, Oz соответственно;

4). Пусть даны две плоскости

,

=(А₁; В₁; С₁),

,

= (А₂; В₂; С₂).

В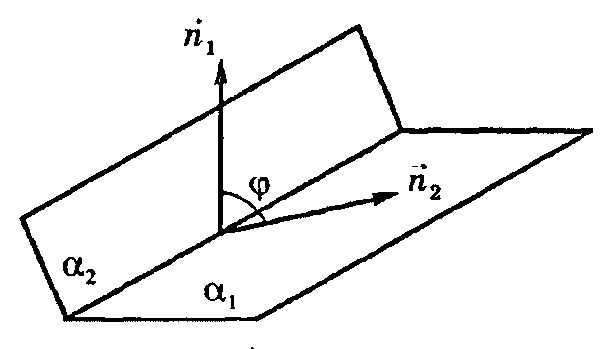 качестве угла φ между плоскостями и принимают угол между их нормальными векторами:

или в координатной форме

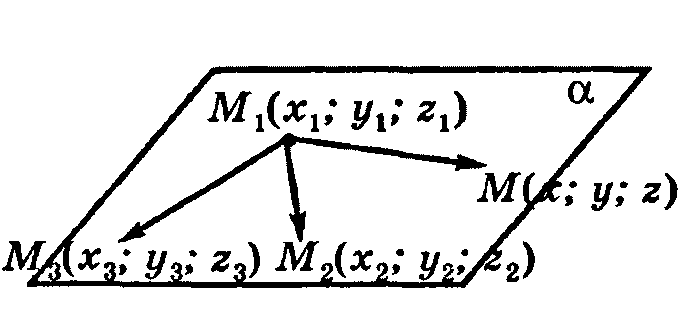
5) Условие перпендикулярности двух плоскостей и : или в координатной форме:

6) Условие параллельности двух плоскостей и :

7) Уравнение плоскости, проходящей через три данные точки

, , :

или в координатной форме:

.

8) Если плоскость α задана общим уравнениемАх + By + Cz + D = 0, а

- некоторая точка пространства, то

есть формула расстояния от точки до плоскости α.

9) Совокупность всех плоскостей, проходящих через одну и ту же прямую, называется пучком плоскостей.

Если и есть уравнения двух различных непараллельных плоскостей, пересечением которых служит некоторая прямая L, а числа α, β - любые не равные одновременно нулю, то

естьуравнение плоскости, проходящей через прямую L. Более того, какова бы ни была проходящая через прямую L плоскость, она может быть определена из пучка плоскостей при определенных значениях α, β.

П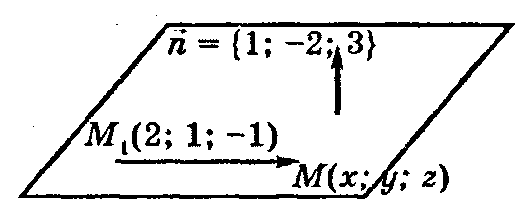 ример. Составить уравнение плоскости, которая проходит через точку и имеет нормальный вектор .

Решение:

Для вывода уравнения плоскости возьмем на этойплоскости точкуМ(х; у; z) с текущими координатами.

Получим вектор . По условию .

Ответ: х - 2у + 3z + 3 = 0.

Пример. Даны две точки и .Составить уравнение плоскости, проходящей через перпендикулярно вектору .

Решение:

По условию вектор является нормальным вектором искомой плоскости .Уравнение плоскости, проходящей через точку перпендикулярно вектору есть

, или

.

Ответ: .

Пример. Составить уравнение плоскости, проходящей через точку параллельно двум векторам .

Решение:

О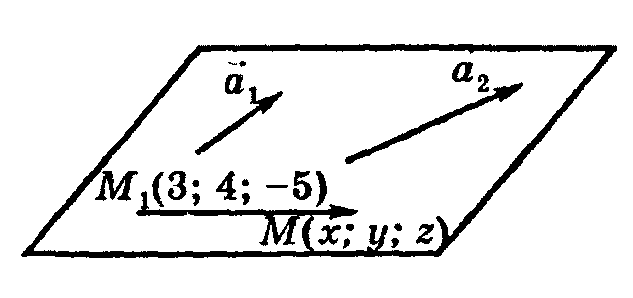 тложим векторы и в плоскости,проходящей через точку и возьмем на искомой плоскости точку М(х; у; z) стекущими координатами.

Получим, что три вектора , , лежат в одной плоскости, т. е. они компланарны.

Условие компланарности есть равенство нулюопределителя, составленного из координат этих векторов.

.

Ответ: .

Пример. Составить уравнение плоскости, проходящей через точки и параллельновектору .

Р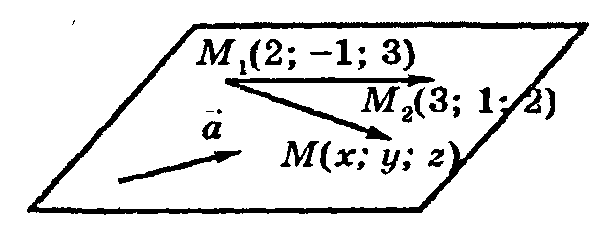 ешение:

Отложим вектор и точку М (х; у; z) с текущими координатами в плоскости, проходящей через точки , . Получимкомпланарные векторы

,

.

Следовательно, по условию компланарности трех векторов будем иметь:

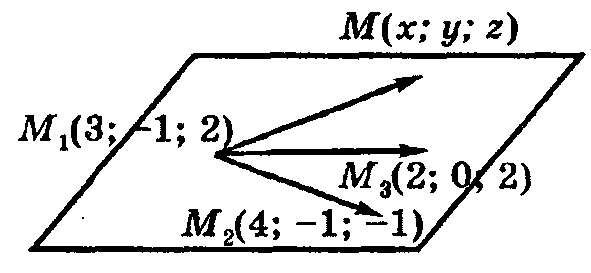
=0, или 7(х - 2) - 7(у + 1) - 7(х - 3), х - у - z= 0.

Ответ: х- у - z = 0.

Пример. Составить уравнение плоскости, проходящейчерез три точки , и .

Решение

Возьмем на плоскости точку с текущими координатами М(х; у; z), будем иметь векторы

,

, . Эти векторы по условию компланарны. Следовательно, равен нулю определитель, составленный из координат этих векторов:

, или Зх + Зу + z - 8 = 0.

Ответ: Зх + Зу+ z - 8 = 0.

Пример. Составить уравнение плоскости, проходящей через точку параллельно плоскости 2х - Зz + 5 = 0.

Решение:

Так как искомая плоскость и данная - параллельны, то у них общий нормальный вектор. Таким образом, получим: через данную точку М₁ провести плоскость, перпендикулярную данному вектору = (2; 0; -3).

,

2(х - 3) + (-3)(z + 7) = 0, 2х - Зz - 27 = 0.

Ответ: 2х - Зz - 27 = 0.

Пример. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям: 2х - у + Зz - 1 = 0,

х + 2у + z = 0.

Решение:

Т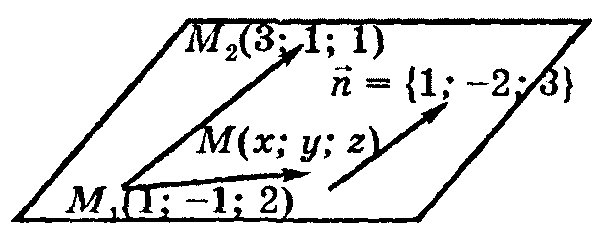 ак как искомая плоскость перпендикулярна плоскостям 2x-y + 3z-l = 0и x + 2y + z = 0, то нормальные векторы = (2; -1; 3) и = (1; 2; 1) и вектор

= (х; у; z) (M - точка с текущими координатами) - компланарны. Следовательно, , или 7х- у- 5z = 0.

Ответ: 7х - у - 5z = 0.

Пример. Составить уравнение плоскости, проходящей через две точки и перпендикулярно к плоскости х - 2у + 3z- 5 = 0.

Решение:

Так как искомая плоскость перпендикулярна плоскости

х - 2у + Зz - 5 =0, то нормальный вектор отложим в плоскости точек , .Возьмем на искомой плоскости еще точку М(х; у; z) с текущими координатами, получим векторы:

.

Три вектора , и - компланарны, поэтому

или 4х - у - 2z = 0.

Ответ: 4х - у - 2z= 0.

Пример. Составить уравнение плоскости, которая проходит через ось Оу и точку

Решение:

Так как плоскость проходит через ось Оу, то ее уравнение можно взять в виде z = kx. Плоскость z = kx проходит через точку , значит, координаты точки удовлетворяют уравнению. Получаем: z = kx, -3 = k • 1, k = -3, Зх + z = 0.

Ответ: Зх + z = 0.

Пример. Составить уравнение плоскости, проходящейчерез точки и параллельно оси Ох.

Решение:

Уравнение плоскости, параллельной оси Ох, имеет вид: By + Cz + D = 0 (коэффициенты В, С, D отличны от нуля).Запишем это уравнение так:

Так какэта плоскость проходит через точки и , то координаты этих точек удовлетворяют искомому уравнению, получаем линейную алгебраическую систему уравнений:

Тогда или у + 4z + 10 = 0.

Ответ: у + 4z + 10 = 0.

П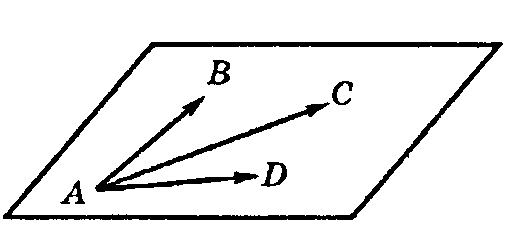 ример. Докажите, что четыре точкиА(1; 2; -1), В(0; 1; 5), С(-1; 2; 1), D (2; 1; 3) лежат в одной плоскости.

Решение:

Рассмотрим векторы . Если оникомпланарны, то данные точки лежат в однойплоскости. = (-1; -1; 6),

= (-2; 0; 2), =(1;-1;4). Тогда

Ответ: данные точки лежат в одной плоскости.