Задания для самостоятельного решения
1. Установить, компланарны ли векторы , , , если:
а)
;
б)
;
а)
.
2. Доказать, что четыре точки А(1; 2; -1), В(0; 1; 5), С(-1, 2; 1), D(2;1;3)лежатв одной плоскости.
3. Вычислить объем тетраэдра с вершинами в точках
А(2; -3; 5), В(0; 2; 1), С(-2; -2; 3),D(3; 2; 4).
4. Аналитическая геометрия
4.1. Прямая на плоскости
1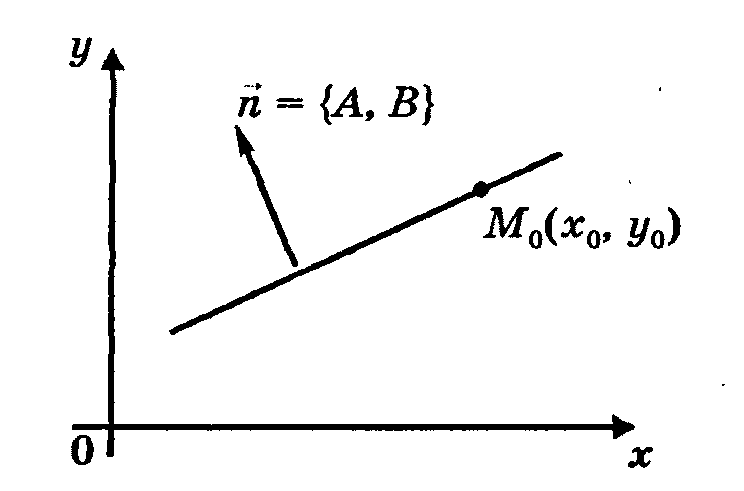
)
- уравнениепрямой, проходящей через
точку 
перпендикулярно
нормальному вектору 
;
2)Ax+By+C=0
–
общее уравнен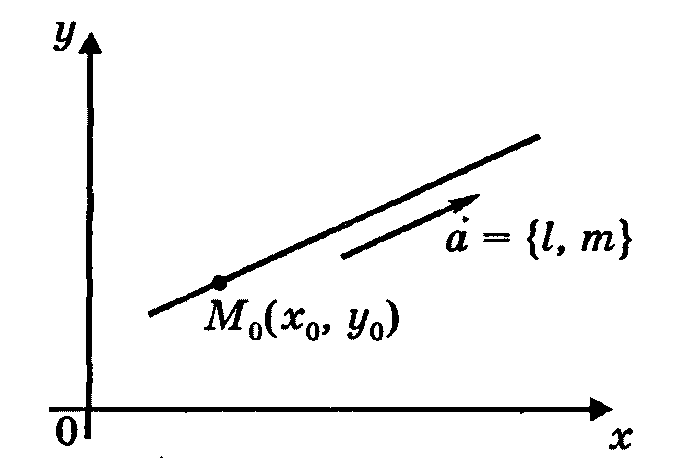
ие
прямой;
3)
– уравнение прямой, проходящей через
точку
параллельно
направляющему вектору 
(каноническое
уравнение прямой);
4)
– параметрические уравнения прямой;
5)
– уравнение прямой в отрезках, где a
и b
–
величины направленных отрезков,
отсекаемых на координатных осяхОх и
Оу соответственно;
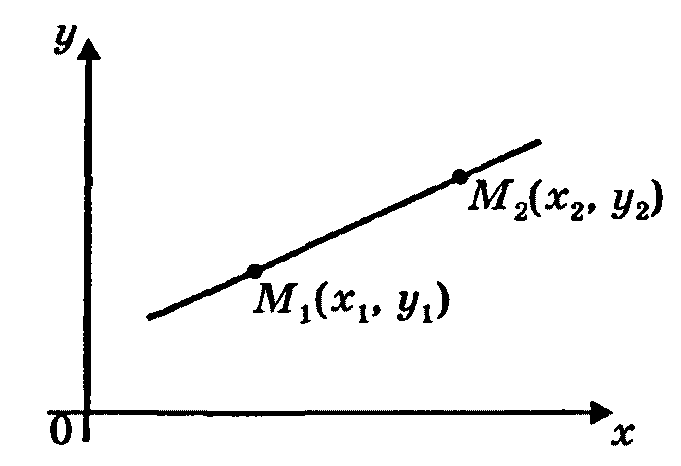
6)
– уравнение прямой, проходящей через
две данные точки
и
;
7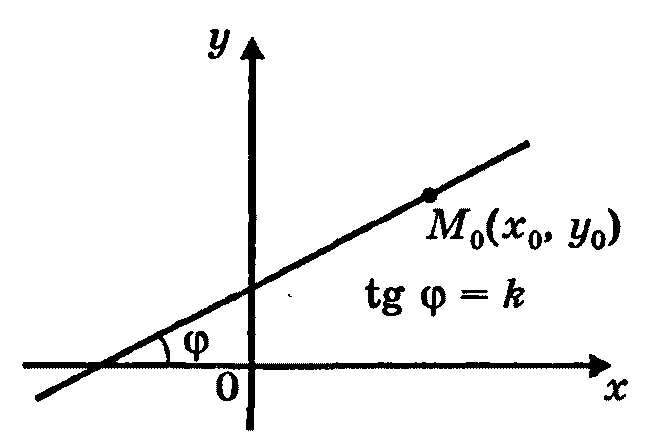
)
– уравнение прямой, проходящей через
точку
,
k - угловой коэффициент прямой, равный
тангенсу угла наклона прямой к
положительному направлению оси Ох;
8) у = kx + b - уравнение прямой с угловым коэффициентом k; b - величина отрезка, отсекаемого прямой на оси Оу;
9)
– тангенс острого угла между двумя
прямыми
и
;
10)
и
– условия параллельности и перпендикулярности
двух прямых
и
;
11)
– расстояние от точки
до
прямой
Ах + By + С = 0;
12)
,
,
≠
–1 - координаты точки М(х, у), делящей
отрезок 
в отношении 
,
,
;
13)
,
– координаты середины отрезка
,
,
.
14)
– уравнение пучка прямых, проходящих
через точку пересечения прямых 
и
.
Пример.
Определить, какие из точек 
лежат на прямой L:
2х - Зу - 3 =
0 и какие не лежат на ней.
Решение:Для того чтобы определить, какие из точеклежат на данной прямой и какие не лежат на ней, надоподставить координаты данных точек в уравнение; если получим верное равенство, то точки лежат на прямой, в противном случае - нет.
;
;
;
;
;
;
Ответ:
точки 
,
и
лежат на данной прямой; точки 
,
и
не лежат на ней.
П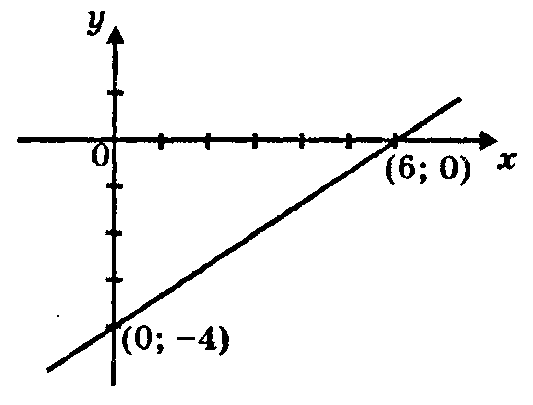
ример.
Определить точки пересечения прямой
2х - Зу - 12 = 0 с координатными осями и
построить эту прямую на чертеже.
Решение: Пусть х = 0, у = –4, (0; –4);
y = 0, х = 6, (6; 0)
Уравнение прямой в отрезках имеет вид:
Ответ:(6; 0) и (0; –4).
Пример. Найти точку пересечения двух прямых
Зх–4у–29 = 0, 2х + 5у + 19 = 0.
Решение: Так как точка М(х, у) лежит на обеихпрямых, то координаты этой точки должны удовлетворять системе уравнений
y = –5, x = 3
Ответ: М(3; –5).
П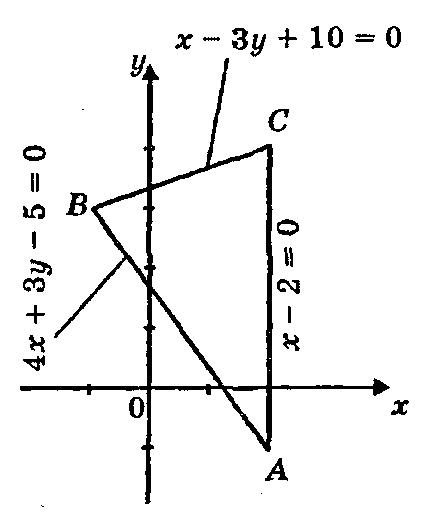
ример.
Стороны АВ, ВС и АС треугольника ABC даны
соответственно уравнениями
4х + 3y–5 = 0,x–3y+10 = 0, x – 2 = 0. Определить координаты его вершин.
Решение:
Найдем точку В пересечения сторон АВ и ВС треугольника ABC.
Точка B(–1; 3).
Найдем точку А пересечения сторон АВ и АС данного треугольника.
Точка А(2; –1).
Найдем точку С пересечения сторон АС и ВС данного треугольника.
точка
С(2;4).
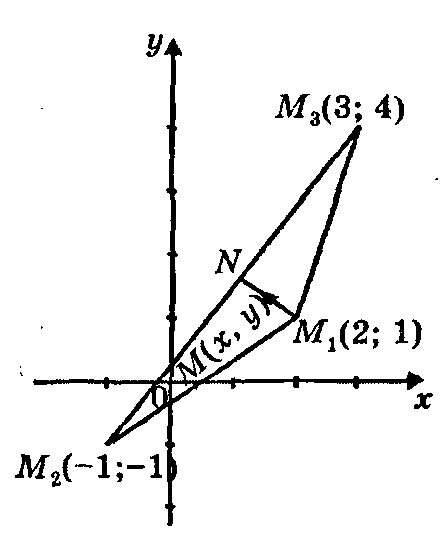
Ответ:A(2; -1), В(-1; 3), С(2; 4).
Пример.
Даны вершины треугольника
,
и
.
Составить уравнения его высот.
Решение:
Пусть
-
высота треугольника 
.
Рассмотрим два вектора 
и
.
По условию эти векторы ортогональны.
Значит, 
.
Аналогично находим остальные высоты треугольника.
Ответ:
.
Пример. Составить уравнениясторон и медиан треугольника с вершинамиА(3; 2),B(5; -2), С(1; 0).
Р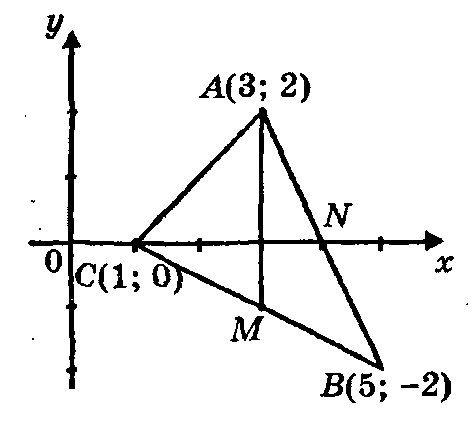
ешение:
1) Воспользуемся уравнением прямой, проходящей через две данные точки
;
Найдем уравнение медианы AM. Для этого найдем координаты точки М - середины отрезка ВС:
.
Уравнение AM:
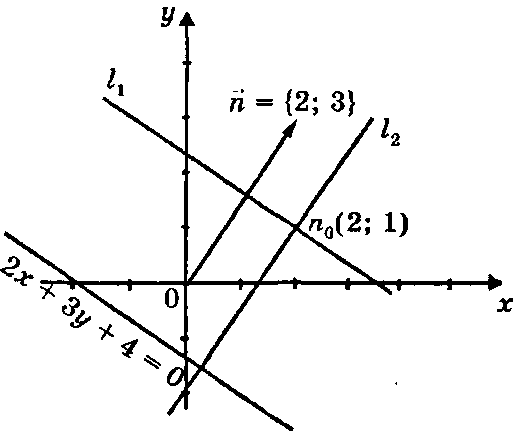
– уравнение медианы, проведенной из
вершины А
2) Найдем уравнения СВ и CN; N(x; у), где
.
Тогда ВС:
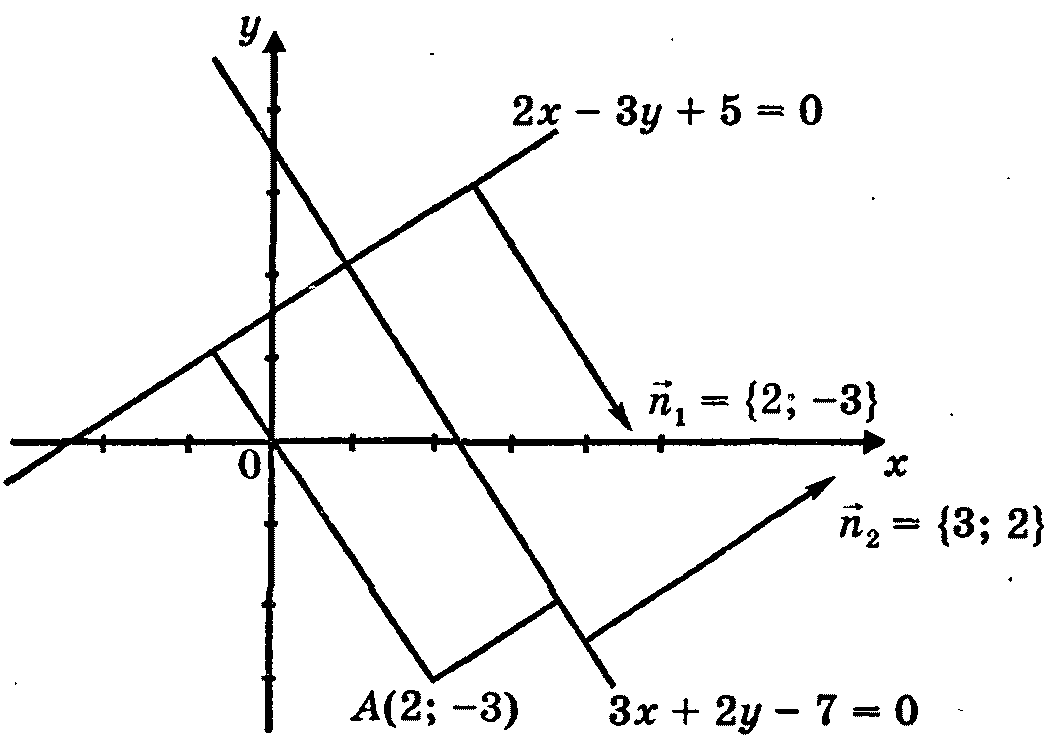
Ответ:
;
BC: x + 2y – 1 = 0;
CN: y = 0;
CA: x – y – 1 = 0;
BF: x + y – 3 = 0.
Пример. Дана прямая 5х + Зу– 3 = 0.
Определить угловойкоэффициент «k»
прямой:
а) параллельной данной прямой;
б) перпендикулярной данной прямой.
Решение:
;
;
.
а)
Угловой коэффициент любой прямой,
параллельной данной, равен
;
;
б)
Угловой коэффициент любой прямой,
перпендикулярной данной, 
Ответ:
a)
;
б) 
Пример.
Дана прямая 2x
+ Зу + 4 = 0. Составитьуравнение прямой,
проходящей через точку
:
а) параллельно данной прямой;
б) перпендикулярно данной прямой.
Решение:
1-й способ.
Нормальный
вектор данной прямой - 
=
(2; 3).
а)
Поэтому уравнение прямой, проходящей
через точку 
,
перпендикулярно вектору 
= (2; 3) будет:
(х - 2) • 2 + (у - 1) • 3 = 0, 2х + Зу - 7 = 0.
б) Уравнение прямой, проходящей через данную точку ; параллельно вектору (перпендикулярноданной прямой), будет:
2-й способ.
Представим
уравнение данной прямой, как уравнение
с угловым коэффициентом, 
.
а)
Тогда уравнение прямой,
проходящей через данную точку
параллельно данной прямой, будет:
или
.
б)
Так как угловой коэффициент прямой,
перпендикулярной данной, равен 
,
то уравнение искомой прямой будет: 
или 
.
Ответ:
а) 
;
б)
.
Пример. Определить угол φ между двумя прямыми:
5х - у + 7 = 0, Зх + 2у = 0.
Решение:За
угол между прямыми возьмем угол между
их нормальными векторами: 
= (5; -1), 
= (3; 2).
Тогда
;отсюда
φ = 45°.
Ответ: φ = 45°.
Пример 14. Установить, перпендикулярны ли прямые
Зх – у + 5 = 0 и х + Зу– 1 =0?
Решение:
3x – y+5 = 0, =(3; –l); x + Зу – 1 = 0, =(1; 3).
Если
,
то прямые перпендикулярны. 
(верно).
Ответ: прямые перпендикулярны.
Пример. Дан треугольник с вершинами А(–2; 0), В(2; 4), С(4; 0). Написать уравнения медианы АЕ, высоты AD и найти длину медианы АЕ.
Решение:
1) Найдем уравнение высоты AD как прямой, проходящей через точку А(–2; 0) перпендикулярно вектору :
2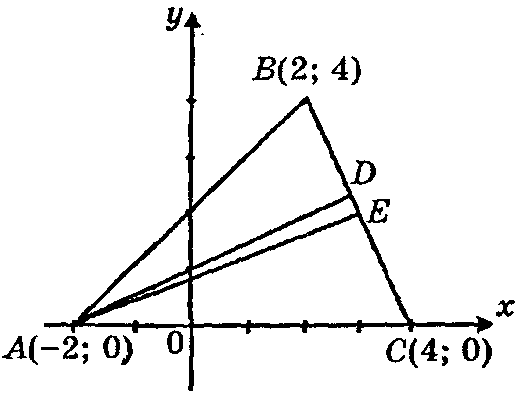
)
Найдем уравнение медианы АЕ как
прямой,проходящей через две точки А и
Е. Координаты точки Е найдем как
координатысередины отрезка СВ:
E(3; 2). Уравнение АЕ:
3) Найдем длину медианы АЕ:
;
,
.
Ответ:
.
Пример. Написать уравнение прямой, проходящей через точку М пересечения прямых 5х – у + 10 = 0 и 8x + 4у + 9 = 0 и параллельной прямой
х + Зу = 0.
Решение:
1-й способ.
1) Найдем координаты точки М пересечения прямых5х – у + 10 = 0 и
8x + 4у + 9 = 0:
2) Прямаяx + Зу = 0 имеет нормальный вектор = (1; 3). Так как уравнение искомой прямой имеет тот же нормальный вектор, то
,
.
2-й способ.
Будем искать уравнение искомой прямой в виде:
или
.
Так
как эта прямая параллельна прямойх + Зу
= 0, то их нормальные векторы коллинеарны:
,
тогда уравнение искомой прямой будет:
,
.
Ответ:
.
Пример. Найти уравнение прямой, проходящей через точку М пересечения прямых х + 2у - 5 = 0, Зх - 2у + + 1 = 0, перпендикулярно к прямой 2х + Зу + 7 = 0.
Решение: Возьмем уравнение искомой прямой в виде:
.
Ее
нормальный вектор 
ортогонален
нормальному вектору 
=
(2; 3) прямой 2х + Зу + 7 = 0. Так как 
,
то 
,
или
.
Тогда уравнение искомой прямой будет:
Зх – 2у+1 = 0.
Ответ: Зх – 2у + 1 = 0.
Пример. Написать уравнение прямой, проходящей через точку А(2; 4) и удаленной от начала координат на расстояние d = 2.
Решение:
Уравнение прямой, проходящей через точку А(2; 4), запишем в виде:
.
Если В = 0, то имеем х = 2; если В ≠ 0,
то
,
где 
.
По условию
.
Ответ:
.