Задания для самостоятельного решения
1. Найти векторное произведение векторов и ,заданных своими координатами.
1)
;
2)
;
3)
.
2. Упростить выражения:
1)
;
2) 
.
3.
Векторы
и
неколлинеарны.
При какихзначениях А, коллинеарны
векторы
и
?
4.
На векторах
и
,
отложенных от одной точки, построен
треугольник. Найти:
1) площадь этого треугольника;
2) длины трех его высот.
12.
Вычислить синус угла, образованного
векторами 
и
.
14.
Сила 
приложена
к точке А(2; -1; 1). Определить момент этой
силы относительно начала координат.
3.6 Смешанное произведение векторов
Определение.
Смешанным произведением векторов
,
и
называется
число, равное скалярному произведению
вектора
и
на
вектор
,
т. е. 
.
Свойства смешанного произведения
.
В
силу этого свойства смешанного
произведения векторов
,
и
обозначают просто 
.
2. Циклическое свойство:
.
3. Если векторы , , в ортогональном базисе заданы своими координатами
,
,
,
то смешанное произведение вычисляется по формуле
.
Геометрический смысл смешанного произведения
1)
Абсолютная величина смешанного
произведения векторов
,
,
численно
равна объему 
параллелепипеда,
построенного на этих векторах, т. е.
.
Крометого, 
,
- объем треугольной пирамиды, построенной
на векторах
,
,
.
2)
Условие компланарности трех векторов.
Необходимым и достаточным условием
компланарности векторов
,
,
является
равенство нулю их смешанного произведения,
т. е. (
,
,
- компланарны)
(
,
,
= 0).
В координатной форме условие компланарности имеет вид:
.
Пример. Найти смешанное произведение векторов , , , заданных своими координатами:
1)
;
2)
;
3)
;
4)
.
Решение.
.
Пример . Проверим, компланарны ли векторы, заданные своими координатами в произвольном базисе:
а)
;
б)
.
Решение. Условие компланарности векторов , , есть
(
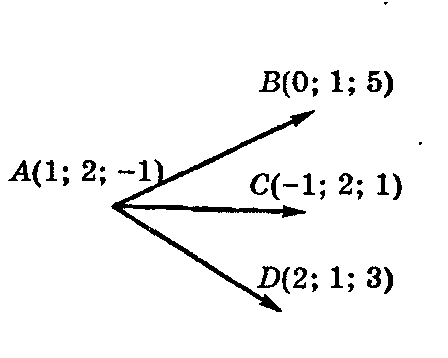= 0).
.
Данные векторы , , компланарны.
2)
.
Данные векторы , , не компланарны
Ответ: а) компланарны;
б) не компланарны.
Пример. Доказать, что четыре точкиА(1;2; -1), В(0; 1; 5), С (-1; 2; 1), D(2; 1; 3) лежат в одной плоскости.
Решение:
Векторы
,
и
имеют
координаты:
,
,
.
Если эти векторы компланарны, то их
смешанное произведение равно нулю:
.
Значит, точки А, В, С, D не лежат в одной плоскости.
Ответ: точки А, В, С, D не лежат в одной плоскости.
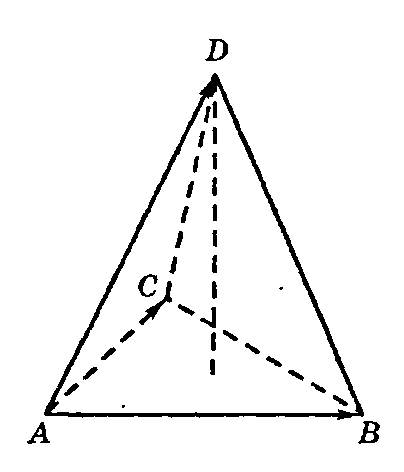
Пример. Найти длину высоты треугольной пирамиды ABCD, опущенной из вершины D на грань ABC. А (2; 2; 2), В (4; 3; 3), С (4; 5; 4), D (5; 5; 6).
Решение: Найдем векторы , и ,совпадающие с ребрами пирамиды, отложенные от вершины А:
,
,
.
Находим смешанное произведение этих векторов:
.
Так как объем пирамиды равен 
части объема параллелепипеда, построенного
на векторах
,
и
,
то 
(куб.
ед.). С другой стороны, 
,
отсюда 
.
Найдем
:
.
.
Тогда
.
Ответ:
.
Пример. Дана пирамида с вершинами А(2; 0; 0), B (0; 3; 0), С (0;0;6) и D (2; 3; 8). Вычислитьее объем и высоту, опущенную на грань ABC.
Решение:
Найдем
векторы
,
и
,
совпадающие с ребрами пирамиды, отложенные
от вершины А: 
,
,
.
Находим смешанное произведение этих векторов:
.
Так
как объем пирамиды равен
части объема параллелепипеда, построенного
на векторах
,
и
,
то 
(куб. ед.)
С другой стороны, и . Найдем
;
и
;
.
Отсюда
.
Ответ:
V = 14,
.
Пример.
Доказать, что векторы 
,
и
компланарны.
Решение:
Составляем смешанное произведение этих векторов:
Так как смешанное произведение оказалось равнымнулю, то, следовательно, векторы компланарны.
Ответ: векторы компланарны.
Пример. Вычислить объем пирамиды с вершинами в
точках О(0; 0; 0), А(5; 2; 0), B(2; 5; 0), С(1; 2; 4).
Решение.
Рассмотрим
векторы 
,
,
.
(куб.
ед.).
(При вычислении определителя мы пользовались разложением его по элементам третьего столбца).
Ответ: 14.