Задания для самостоятельного решения
1.
Даны векторы 
,
,
вычислить:
1)
;
2) 
;
3)
;
4)
;
5) 
;6)
.
2. В треугольнике ABC даны длины его сторон:
,
,
.
Найти скалярныепроизведения векторов
и
.
3. Найти скалярное произведение векторов и , если
1)
;
2)
3)
4)
и
сонаправлены;
5)
и
противоположно
направлены.
4. Найти скалярное произведение векторов и , заданных своими координатами:
1)
;
2)
;
3)
.
5.
Даны три вектора:
.
Вычислить:
1)
;
2)
;
3)
.
6. Найти значение α, при которых следующие векторы взаимно перпендикулярны:
а)
и
;
б)
.
7.
Под действием силы 
точкапереместилась
из 
в
D(-l; 2; 1). Найти работу силы
.
8. Дан треугольник с вершинами в точкахА(1; –2),В(5; –4), С(–2; 0). Найти вектор параллельный биссектрисе угла А.
3.5 Векторное произведение векторов
Определение. Векторным произведением двух векторов и называют третий вектор , удовлетворяющий условиям:
1)
,
где φ – угол между
и
(0 ≤ φ
≤ π);
2) вектор ортогонален векторам и ;
3) векторы образуют правую тройку векторов.
Векторное
произведение векторов
и
обозначают
или
.
Если хотя бы один из сомножителей равен , товекторное произведение по определению есть нулевой вектор.
Понятие
векторного произведения родилось в
механике. Если вектор
изображает приложенную в некоторой
точке Р силу, а вектор
идет из некоторой точки О в точку Р, то
вектор 
представляет
собой момент силы
относительно точки О.
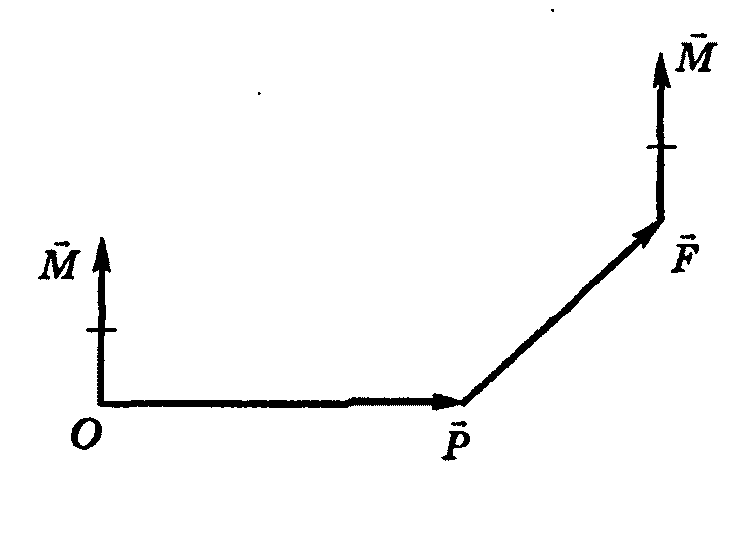
Геометрический смысл векторного произведения
1. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
2. Длина (модуль) векторного произведения равна площади S параллелограмма, построенного на приведенных к общему началу векторах и , т. е.
Алгебраические свойствавекторного произведения
Векторное умножение обладает следующими четырьмя свойствами:
1)
-свойство
антикоммутативности;
2)
-свойство
ассоциативности относительно числового
множителя;
3)
-свойстводистрибутивности
относительно суммы векторов;
4)
для
любого вектора
.
Если
и
– векторы, заданные своими координатами
в прямоугольном базисе, торазложение
векторного произведения
в
том же базисе имеет вид:
,
или
.
Пример.
Векторы
и
образуют угол 
.
Зная, что 
и 
,
вычислить:
;
2)
;
3)
.
Решение.
По определению скалярного произведения имеем:
.
.
.
Ответ: 1) 3; 2) 27; 3)300.
Пример.
Даны векторы 
и
.
Найти координаты векторных произведений:
; 2)
;
3) 
.
Решение.
,
.
.
.
Ответ: 1) (5;1;7); 2) (10;2;14); 3) (20;4;28).
Пример. Даны вершины треугольника А(1;–1; 2),В(5;–6;2) и С(1;3;–1). Вычислить длину его высоты, опущенной из вершины В на сторону АС.
Решение:
Находим
и 
.
.
;
.
.
Тогда
длина искомой высоты
.
Ответ: 5.
Пример. Даны точки А(1; 2; 0), B(3; 0; –3), С(5; 2; 6).
Вычислить площадь треугольника ABC.
Решение:
Находим
векторы
и
:
;
.
.
(кв. ед.).
Ответ: 14.
Пример.
Сила 
приложена
к точке А(4; 2; 
3).Определить
величину и направляющие косинусымомента
этой силы относительно точки С(2; 4; 0).
Решение:
,
поэтому найдем координаты 
и 
:
,
.
Величина М – это его модуль:
.
Найдем
орт вектора
:
.
Ответ:
28;
.