Павлидис В.Д.

Практикум

по алгебре и аналитической геометрии

Оренбург 2011

ББК 22.12

УДК 517.51

Рецензенты:

А.И. Сердюк – доктор технических наук, профессор

С.Е. Тычинина – кандидат физико-математических наук, доцент

Павлидис В.Д.

Практикум по алгебре и аналитической геометрии.- Оренбур: Издательский центр ОГАУ.

Данное учебное пособие представляет собой методические разработки практических занятий по разделу «Алгебра и аналитическая геометрия» для студентов - бакалавров специальностей «АСОИ», «БАС»,«Технические системы в агробизнесе»,«Электрооборудование и электротехнологии», «Технический сервис в агропромышленном комплексе». Пособие содержит основной теоретический материал покаждой изучаемой теме, образцы подробного решения типовых задач, задачи для самостоятельного решения. Это позволяет использовать его как для аудиторной работы, так и для самостоятельной работы студентов, а так же для подготовки к текущему и итоговому тестированию.

Содержание

1.Линейная алгебра……………………………………………… 5

1.1 Матрицы………………………………………………………. 5

1.2. Определители…………………………………………………10

1.3. Линейное (векторное) пространство……………………… 14

1.4. Системы линейныхалгебраических уравнений………... 15

1.5. Линейные операторы……………………………………….. 29

2. Комплексные числа…………………………………………… 33

2.1. Алгебраическая форма записи комплексных

чисел……………………………………………………………….. 33

2.2. Тригонометрическая форма записи комплексных

чисел………………………………………………………………… 36

2.3. Показательная форма записи комплексных чисел……... 40

3. Векторная алгебра……………………………………………… 42

3.1. Линейные операции над векторами……………………….. 42

3.2. Линейная комбинация векторов…………………………… 47

3.3 Прямоугольная декартова система координат…………… 52

3.4 Скалярное произведение векторов…………………………. 55

3.5 Векторное произведение векторов………………………….. 60

3.6 Смешанное произведение векторов………………………… 64

4. Аналитическая геометрия……………………………………... 68

4.1. Прямая на плоскости………………………………………… 68

4.2 Плоскость……………………………………………………….. 76

4.3. Прямая и плоскость в пространстве……………………….. 82

4.4 Линии второго порядка………………………………………. 89

Литература………………………………………………………….. 99

1. Линейная алгебра

1.1 Матрицы Операции над матрицами

Определение. Матрицей размера (или - матрицей) называется прямоугольная таблица чисел

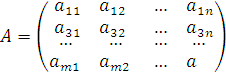, состоящая из m строк и n столбцов.

Определение. Суммой - матриц и называется матрица того же порядка,каждый элемент которой равен сумме соответственных элементов матриц А и В:

Определение. Произведением αA матрицы на действительное число α называется матрица ,получающаяся из матрицы А умножением всех ее элементов наα: .

Определение. Произведением - матрицы на – матрицу называется - матрица , элемент которой , стоящий в i-й строкеи j-м столбце, равен сумме произведений соответственных элементов i-й строки матрицы Aи j-го столбца матрицы B:

Матрицы перемножить возможно тогда, когда числостолбцов матрицы А равно числу строк матрицы В.

Для матриц одинакового размера справедливы свойства следующих алгебраических операций:

1) А + В = В + А; 2) А + (В + С) = (А + В) + С;

3) (α + β)А = αА + βА;

4) α(А + В) = αА + βВ;

5)(αβ)А = α(βА);

6)А(ВС) = (АВ)∙С;

7)А(В + С) = АВ+АС.

Определение. Нуль-матрицей называется матрица О, все элементы которой равны нулю.

Определение. Единичной матрицей Е называетсяквадратная матрица, на главной диагонали которой стоят единицы, а остальные элементы равны нулю.

Пример:

Справедливы равенства: А + 0=А; АЕ = ЕА = А.

Обратная матрица

Определение. Квадратная матрица (m = n) называется вырожденной (особой), если ее определитель равен нулю, и невырожденной (неособенной) в противном случае.

Определение. Если А– невырожденная матрица, то существует, и притом единственная, матрица такая, что

,

где Е - единичная матрица того же размера, что иматрицы А и .

Матрица называется обратной к матрице А.

Определение. Назовем матрицу присоединенной, если она является транспонированной матрицей, составленной из алгебраических дополнений соответствующих элементов матрицы А.

Если матрица А - невырожденная, то

Пример. Найти сумму матриц А и В, если

Решение:

Ответ:

Пример. Вычислить матрицу 2А + 5В, если

.

Решение:

Ответ:

Пример. Найти произведение АВ матрицы-строки на матрицу

Решение:

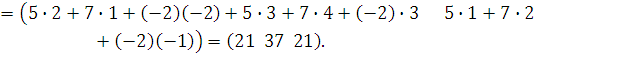
Ответ: матрица-строка размера (1 х 3) –(21 37 21).

Замечание. (1 x3)- матрица при умножении на (3 х 3) - матрицу дает(1 x3)- матрицу.

Пример. Найти присоединенную матрицу для матрицы

Решение:

Присоединенная матрица является транспортированной матрицей из алгебраических дополнений данной матрицы.

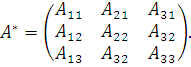
Для данной матрицы

Итак, присоединенная матрица равна

.

Ответ:

Пример. Найти матрицу , обратную к матрице А

Из предыдущего примера.

Решение: Так как , то найдем

Тогда