
- •Факультет: экономики и социального управления кафедра: социальные, естественно-научные и правовые дисциплины дисциплина: математический анализ
- •Контрольная работа должна быть сдана согласно графику.
- •Контрольная работа
- •Контрольные вопросы к экзамену.
- •Литература
- •Баврин и.И., Матросов в.Л. Высшая математика. Учебник. – м.: Владос, 2002. Рек.
- •Сборник задач по высшей математике для экономистов. Учеб. Пос. / Под ред. В.И. Ермакова. – м.: Информатика – м, 2003. Рек.
- •Шипачев в.С. Высшая математика. Учебник. – м.: Высш. Шк., 2001. Рек.
Факультет: экономики и социального управления кафедра: социальные, естественно-научные и правовые дисциплины дисциплина: математический анализ
Самостоятельная работа над учебным материалом является основной формой обучения студентов заочного отделения. Перед выполнением контрольной работы рекомендуется изучить лекции и рекомендуемую учебную литературу.
В данных методических указаниях предложено 20 вариантов контрольной работы. Номер варианта каждого студента соответствует его номеру в учебном журнале. Если в группе по списку более 20 человек, то 21 делает 1вариант, 22 – 2 вариант, и т.д.
Работа должна быть написана от руки четким аккуратным почерком или набрана с использованием средств оргтехники, чертежи должны быть аккуратно выполнены по линейке. Компьютерный вариант текста должен быть представлен 14 разряженным шрифтом Times New Roman c полуторным интервалом между строк. Работа выполняется на белых или в клетку стандартных листах бумаги формата А-4. Лист работы должен иметь поля не менее: верхнее 2см, нижнее 2см, левое 2,5см, правое 1,5см. листы должны быть пронумерованы в правом верхнем углу. Первая страница (титульный лист) не нумеруется, но считается как первая страница работы, на последней странице перечисляется список используемой литературы.
Контрольная работа должна быть сдана согласно графику.
При выполнении контрольной работы надо указать № задания и целиком написать условие с данными соответствующими конкретному варианту. Ответы на вопрос задания должны быть ясно выделены.
Например: Иванов В.С. седьмой по списку в журнале, значит, выполняет вариант №7, т.е. все данные в заданиях берет под номером семь.
Контрольная работа
Задание № 1. Найти предел функции:
1.а)![]() ;
б)
;
б)![]() 2.а)
2.а)![]() ;
б)
;
б)![]()
3.а)![]() ;
б)
;
б)![]() 4.а)
4.а)![]() ;
б)
;
б)![]()
5.а)![]() ;
б)
;
б)![]() 6.а)
6.а)![]() ;
б)
;
б)![]() 7.а)
7.а)![]() ;
б)
;
б)![]() 8.а)
8.а)![]() ;
б)
;
б)![]() 9.а)
9.а)![]() ;
б)
;
б)![]() 10.а)
10.а)![]() ;
б)
;
б)![]()
11.а)![]() ;
б)
;
б)
![]() 12.а)
12.а)![]() б)
б)
![]() 13.а)
13.а)![]() ;
б)
;
б)
![]() 14.а)
14.а)![]() ;
б)
;
б)
![]() 15.а)
15.а)![]() б)
б)![]() 16.
а)
16.
а)![]() ;
б)
;
б)![]() 17.а)
17.а)![]() ;
б)
;
б)![]() .
18.
а)
.
18.
а)![]() б)
б)![]() 19а)
19а)![]() б)
б)
![]() 20.а)
20.а)![]() б)
б)![]() .
.
Задание № 2. Найти производные функций, определив ее вид:
1.
![]() ;
;
![]() ;
2.
;
2.
![]() ;
;
![]() ;
;
3.
![]() ;
;
![]() 4.
4.
![]() ;
;
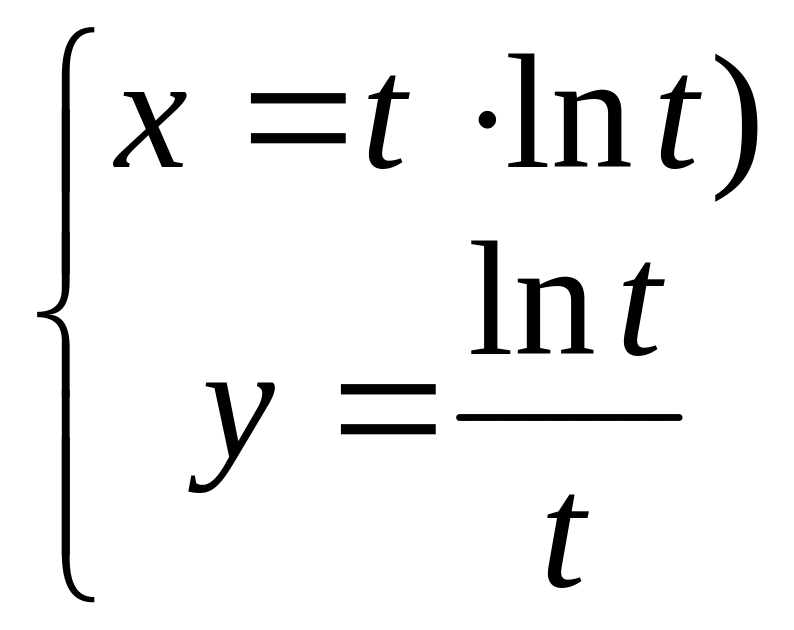 ;
;
5.
![]() ;
;
![]() 6.
6.
![]() ;
;
![]() ;
;
7.
![]() ;
;
![]() 8.
8.
![]() ;
;
 ;
;
9.
![]() ;
;
![]() 10.
10.
![]() ;
;
 ;
;
11.
![]() ;
;
![]() ;
12.
;
12.
 ;
;
![]()
13.
![]() ;
;
![]() ;
14.
;
14.
 ;
;
![]() ;
;
15.
![]() ;
;
 ;
16.
;
16.
![]() ;
;
![]()
17.
![]() ;
;
![]() ;
18.
;
18.
![]() ;
;
![]()
19.
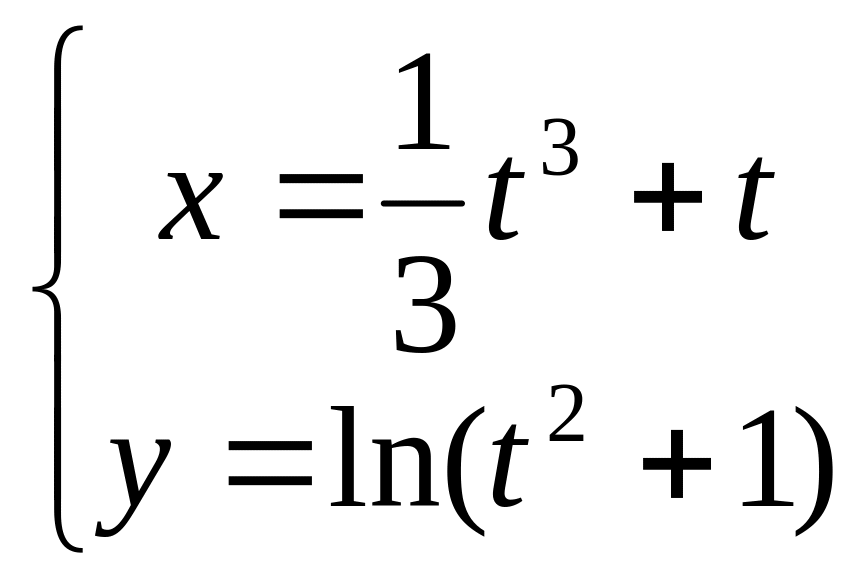 ;
;
![]() 20.
20.
![]() ;
;
![]()
Задание № 3. Исследовать методами дифференциального исчисления функцию и построить ее график.
1.
![]() ;
2.
;
2.
![]() ;
3.
;
3.
![]() ;
4.
;
4.
![]() ;
5.
;
5.
![]() ;
;
6.
![]() ;
7.
;
7.
![]() ;
8.
;
8.
![]() ;
9.
;
9.
![]() ;
10.
;
10.
![]() ;
11.
;
11.
![]() ;
12.
;
12.
![]() ;
13.
;
13.
![]() ;
14.
;
14.
![]() ;
15.
;
15.
![]() ;
16.
;
16.
![]() ;
17.
;
17.![]() ;
18.
;
18.
![]() ;
19.
;
19.
![]() ;
20.
;
20.
![]() .
.
Задание № 4. Найти частные производные первого и второго порядка функции, исследовать ее на экстремум.
(zx; zy; zxx; zyy; zxy)
1. z = x2 – xy – y; 11. z = x2 – y2;
2. z = xy(1 – x – y); 12. z = 3x +6у – х2 – хy + y2;
3. z = x2 + y2 + ху – 4x – 5у; 13. z = x2 – 2y2 -2x;
4. z = 2x2 – xy – y2; 14. z = x + 2xy – y;
5. z = x2 + y2 – 15xy; 15. z = x2 – y2 – 2y;
6. z = x3 – y3 – 3хy; 16. z = 2xy – 4x – 2y;
7. z = x2 + y2 +xy – 4x – 5y; 17. z = xy(1 – х – у);
8. z = x3 – y3 – 3xy; 18. z = 3x + 6y – x2 –xy + y2;
9. z = 2x3 – xy2 + 5x2 + y2; 19. z = 2x2 + 3y2 +4x;
10. z = x2 + 3y2 – 2x + 2; 20. z = 2x3 – ху2 + 5х2 + у2.
Задание № 5. Вычислить неопределенный интеграл:
1.
a)
ln(х2
+ 4)dx
;
![]() 2.
xcos(x)dx;
2.
xcos(x)dx;
![]() 3.
xe-xdx;
3.
xe-xdx;
![]()
4.
x·3xdx;
![]() 5.
arccos(x)dx;
5.
arccos(x)dx;
![]() ;
6.
x·arctg(x)dx;
;
6.
x·arctg(x)dx;
![]()
7.
arctg(x)dx;
![]() 8.x3exdx
8.x3exdx
![]() 9.
x2ln(1+x)dx;
9.
x2ln(1+x)dx;
![]()
10.
exsin(x)dx;
![]() 11.
x3sin(x)dx;
11.
x3sin(x)dx;
![]() 12.
x2e-xdx;
12.
x2e-xdx;
![]()
13.
ln(x2+1)dx;
![]() 14.
ln2xdx;
14.
ln2xdx;
![]() 15.xsin(2x)dx;
15.xsin(2x)dx;
![]()
16. e2xx2dx;
![]() 17.
17.![]() ;
;
![]() 18.
exdx;
18.
exdx;
![]() ;
;
19.
(2x2+x)ln(x)dx;
![]() 20.
xln(x)dx;
20.
xln(x)dx;
![]() .
.
Задание № 6. Найти площадь фигуры, ограниченной кривыми:
1. у = х2+1; ух = 2; у = 0, х = 0, х = 2; 6. у = ex, x = 0, x = ln3, у = 0;
2.
y = x
и
y = x3;
7.
y
= cosx, y = 0,
![]() ,
,
![]() ;
;
3. y
= tgx, x =0,![]() ,
у
= 0 8.
y = sinx,
,
у
= 0 8.
y = sinx,
![]() ,
,![]() ;
;
4. y = lnx, y = 0, х = e3; 9. y = 4x2, y = 4/x, y = 0, x = 4;
5. y
=
![]() ,
x =2, x = 5, y = 0; 10.
y = 4x – x2,
y = x
,
x =2, x = 5, y = 0; 10.
y = 4x – x2,
y = x
11. у = е2х, у=0, x = 0, x = 1; 16. y2 = x, y = x2;
12. y = tgx, x = 0, y = 1; 17. y = sinx, x = 0, y = 3/2;
13. y = 9х2 – 6х +1, y =0, х = 0; 18. y = √2x, 0 ≤ y ≤ 4;
14. y = 3x, y2 = 9x; 19. y = 4 – x2, y = 3x;
15. y = 2 – x2, y = 4 – 3x, x = 0; 20. y = (x+2)2, x = 0, y =9.
Задание № 7. Исследовать ряд на сходимость
1.
![]() ;
2.
;
2.
![]() ;
3.
;
3.
![]() ;
4.
;
4.
![]() ;
5.
;
5.
![]() ;
;
6.
![]() ;
7.
;
7.
![]() ;
8.
;
8.
![]() ;
9.
;
9.
![]() ;
10.
;
10.
![]() ;
;
11.
![]() ;
12.
;
12.
![]() ;
13.
;
13.
![]() 14.
14.
![]() 15.
15.
![]() ;
;
16.
![]() ;
17.
;
17.
![]() ;
18.
;
18.
![]() ;
19.
;
19.
![]() ;
20.
;
20.
![]() .
.
Задание № 8. Решить дифференциальное уравнение и найти его частное решение при начальных условиях:
1. y// + 5y/ + 4y = 0 у(0) = 0, у/(0) = 1; 2. y// + 2y/ = 0 у(0) = -2, у/(0) = 1;
3. y// + 6y/ + 10y = 0 у(0) = 0, у/(0) =-2; 4. y// – 2y/ – 3y = 0 у(0) = 2, у/(0) = 0;
5. y// + 4y/ + 4y = 0 у(0) = -1, у/(0) =1; 6. y// – y/ – 2y = 0 у(0) = 2, у/(0) = 1;
7. y// – 2y/ = 0 у(0) = 1, у/(0) = 2; 8. y// + y/ = 0 у(0) = -1, у/(0) = 1;
9. y// + 2y/ + 2y = 0 у(0) = 1, у/(0) = -1; 10. y// – 3y/ – 4y = 0 у(0) = 1, у/(0) = 0;
11. y// + 6y/ + 9y = 0 у(0) = -2, у/(0) = -1; 12. y// + 2y/ + 2y = 0 у(0) =-1, у/(0) =2;
13. y// – 4y/ + 3y = 0 у(0) = 2, у/(0) = 1; 14. y// – 2y/ + 5y = 0 у(0) =-1, у/(0) = 1;
15. y// – 5y/ + 6y = 0 у(0) = 1, у/(0) =-2; 16. y// – 4y/ + 13y = 0 у(0) = 1, у/(0)= 3;
17. y// + 2y/ + 2y = 0 у(0) =-1, у/(0) = 2; 18. y// – 6y/ + 9y = 0 у(0) =1, у/(0) = 4;
19. y// – y/ – 2y = 0 у(0) = 2, у/(0) = -5; 20. y// – 3y/ + 2y = 0 у(0) = 1, у/(0) =4;
