
- •Дифференциальные уравнения первого порядка
- •1. Уравнения с разделяющимися переменными
- •2. Однородные уравнения
- •Ду в полных дифференциалах
- •Найти общее решение или общий интеграл уравнения
- •I.Вопросы по теме « Дифференциальные уравнения первого порядка»
- •Знать с доказательством:
- •2. Письменный « Конспект лекций по высшей математике» кн 2
- •3. Пискунов «Дифференциальные и интегральные исчисления», т 2
- •Б). Лнду вида
- •Метод Лагранжа
- •Решить лнду методом Лагранжа
- •II. Вопросы по теме:
- •III.Системы дифференциальных уравнений
- •1. Письменный « Конспект лекций по высшей математике» кн 2
- •2. Пискунов «Дифференциальные и интегральные исчисления», т 2
- •III. Вопросы по теме: « Системы дифференциальных уравнений»
- •1. Письменный « Конспект лекций по высшей математике» кн 2
- •Градиент
- •Найти градиент скалярного поля
- •Поток вектора
- •Дивергенция
- •Найти дивергенцию векторного поля
- •Циркуляция
- •Тема № 3 Ряды
- •2. Письменный « Конспект лекций по высшей математике» кн 2
- •3. Пискунов «Дифференциальные и интегральные исчисления», т 2 Знакоположительные ряды
- •Знакопеременные ряды
- •Степенные ряды
- •План нахождение области сходимости:
- •Тема № 4 Ряды Фурье Литература:
- •3. Пискунов «Дифференциальные и интегральные исчисления», т 2
- •Тема 5:Теория функции комплексной переменной ( тфкп)
- •Комплексные числа (повторение)
- •2) Тригонометрическая форма
- •3) Показательная форма комплексного числа
- •II. Функция комплексного переменного
- •2. Формула Ньютона –Лейбница
- •3. Теорема Коши для односвязной области
- •4. Интегральная формула Коши
- •1. Особые точки.
- •2. Вычеты
- •Вопросы по теме:
- •Тема 6: Операционные исчисления
- •2. Пискунов «Дифференциальные и интегральные исчисления», т 2
- •1. Оригиналы и их изображения
- •Нахождение оригинала по изображению
- •2. Применение преобразования Лапласа к интегрированию линейных неоднородных дифференциальных уравнений
- •Вопросы по теме:
Б). Лнду вида

Общий вид |
Общее решение + |
где - общее решение соответствующего однородного уравнения |
y* - частное решение ЛНДУ
где
|
- кратность корня: если
если
где k1,2 – корни соответствующего характеристического уравнения. |
№94.
 .
№95.
.
№95.
 .
.
№96.
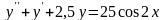
№97.
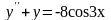 ,
если при
,
если при
 ,
.
,
.
№98.
 ,
если при
,
если при
 ,
.
,
.
№99.

Метод Лагранжа
Правило интегрирования ЛНДУ методом Лагранжа
Находим решение соответствующего ЛОДУ в виде

Устанавливает ожидаемый вид
 ,
,

Составляем СЛАУ

4. Находим
решение СЛАУ

5. Интегрируем
и находим

Записываем общее решение

Решить лнду методом Лагранжа
№100.
 .
.
№101.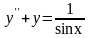 .
№102.
.
№102.
 .
.
№103.
 .
№104.
.
№104.
 .
.
№105.
 №106.
№106.
 .
.
№107.
 .
№108.
.
№108.
 .
.
II. Вопросы по теме:
« Дифференциальные уравнения второго и высших порядков»
Какое уравнения называется ДУ высшего порядка?
Формы записи обыкновенного ДУ второго (n- го) порядка
Что называется решением ДУ n – порядка?
Как называется график решения ДУ?
Что значит «решить ДУ n – порядка»?
Что называется общим решением ДУ второго (n- го) порядка?
Что называется частным решением ДУ второго (n- го) порядка?
Что называется общим интегралом ДУ второго (n- го) порядка?
Что называется частным интегралом ДУ второго (n- го) порядка?
В чем заключается задача Коши для ДУ второго (n- го) порядка?
Теорема существования и единственности решения задачи Коши для второго (n- го) порядка?
Общий вид ДУ допускающих понижение степени и методы их решения
Определение линейного дифференциального уравнения n – го порядка. Виды ЛДУ.
Линейные однородные дифференциальные уравнения (ЛОДУ)
Теорема о частных решения ЛОДУ второго порядка
Определение линейно независимых и линейно зависимых частных решений ЛОДУ
Определение ФСР и ее свойства (основные теоремы)
Теорема о структуре общего решения ЛОДУ второго (n- порядка) порядка.
ЛОДУ второго и высших порядков с постоянными коэффициентами, основные определения.
Общий вид частных и общего решения ЛОДУ второго порядка с постоянными коэффициентами в случае: а)действительных и различных; б) действительных и равных; в) комплексно сопряженных корней характеристического уравнения.
Сформулируйте правило интегрирования ЛОДУ n- порядка с постоянными коэффициентами.
ЛНДУ. Общий вид ЛНДУ второго (n- го) порядка.
Теорема о структуре общего решения ЛНДУ n – порядка
ЛНДУ второго порядка с постоянными коэффициентами
В чем сущность метода неопределенных коэффициентов? Для какого типа уравнений он применяется?
Специальные виды правой части ЛНДУ с постоянными коэффициентами.
Ожидаемая форма частного решения y* ЛНДУ с постоянными коэффициентами, если f(x) имеет первый или второй специальный вид
Теорема о наложении частных решений.
Теорема о структуре общего решения ЛНДУ
В чем состоит метод вариации произвольных постоянных?
При интегрировании каких дифференциальных уравнений целесообразно применять этот метод?

 ,
, - из условия
- из условия ,
,
 - многочлены степени l,
l
=
- многочлены степени l,
l
=
 ,
n,m
ϵ
Z
,
n,m
ϵ
Z ,
то
=
0;
,
то
=
0; ,
то
=
1
,
то
=
1