Работа 20. Измерение коэффициента Пуассона

1. Цель работы

Изучение процессов в идеальных газах, измерение коэффициента Пуассона .

13. Краткая теория

Коэффициент Пуассона  – это параметр адиабатного процесса. Он входит в известное уравнение Пуассона, описывающее адиабатный процесс в идеальном газе. Рассмотрим, что это за уравнение и как оно выводится.

Адиабатным называется процесс, протекающий без теплообмена с окружающей средой, 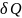=0.

На практике он может быть осуществлен в системе, окруженной теплоизоляционной оболочкой, но поскольку для теплообмена необходимо некоторое время, то адиабатным можно считать также процесс, который протекает так быстро, что система не успевает вступить в теплообмен с окружающей средой. Для получения уравнения адиабатного процесса удобно начать с первого закона термодинамики.

Согласно первому закону термодинамики количество теплоты , сообщённое системе, расходуется на увеличение внутренней энергии dU и на выполнение системой работы :

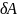. (3.1)

Увеличение внутренней энергии идеального газа в случае изменения его температуры на 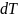равно:

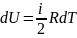. (3.2)

Здесь i – число степеней свободы молекулы, под которым подразумевается число независимых координат, определяющих положение молекулы в пространстве: i = 3 для одноатомной молекулы, i = 5 – для двухатомной, i = 6 – для многоатомной, R – универсальная газовая постоянная, .

Работа газа определяется выражением:

. (3.3)

Для адиабатного процесса из формул (3.1) – (3.3) следует:

. (3.4)

Это – дифференциальное уравнение, связывающее два дифференциала dT и dV. Но в нём присутствуют не функции T и V, а функция P. Поэтому надо либо функцию P выразить через T и V, либо один из дифференциалов dT или dV выразить через дифференциал dP. Последнее можно сделать, продифференцировав уравнение Клапейрона – Менделеева.

. (3.5)

Подставив (3.5) в (3.4), получим:

.

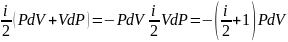Решение этого дифференциального уравнения можно получить методом разделения переменных. Для этого разделим обе части уравнения на PV.

.

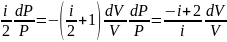Проинтегрировав левую и правую часть получаем:

.

Потенцирование этого уравнения даёт:

.

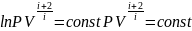Последнее уравнение и есть упоминавшееся выше уравнение Пуассона. Для краткости в нём показатель степени обозначают одной буквой  и называют показателем адиабаты или коэффициентом Пуассона. Итак, уравнение Пуассона имеет вид:

. (3.6)

Интересно, что коэффициент Пуассона можно выразить через теплоёмкости газа при постоянном давлении и при постоянном объёме.

Отметим сначала, что физическая величина «теплоёмкость» бывает трёх типов: полная, удельная и молярная. Полная теплоёмкость C есть величина, равная количеству теплоты, которое необходимо сообщить данной системе для увеличения её температуры на один градус. Это значит, что

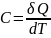. (3.7)

Удельной теплоёмкостью вещества называется величина c, равная теплоёмкости единице массы этого вещества.

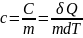. (3.8)

Теплоёмкость одного моля вещества называется молярной теплоемкостью:

, (3.9)

где  – количество молей.

Если газ нагревать при постоянном объёме, то и согласно (3.1) всё полученное газом количество теплоты расходуется только на увеличение его внутренней энергии . Тогда из (3.7) и (3.2) следует, что молярная теплоёмкость идеального газа при постоянном объёме равна:

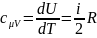. (3.10)

Если газ нагревать при постоянном давлении, то полученное газом количество теплоты расходуется на увеличение внутренней энергии dU и выполнение работы .

.

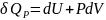Тогда молярная теплоёмкость идеального газа при постоянном давлении равна:

. (3.11)

Используя уравнение Клапейрона – Менделеева, можно доказать, что

.

Поэтому из (3.10) и (3.11) следует, во-первых, уравнение Майера

, (3.12)

а во-вторых,

. (3.13)

Поделив (3.13) на (3.10), получим интересный результат:

. (3.14)