
- •Лабораторный практикум по физике Часть 5. Квантовая физика
- •Оглавление
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Описание установки.
- •Выполнение работы.
- •Контрольные вопросы
- •Описание установки
- •Выполнение работы
- •Контрольные вопросы
- •Описание установки
- •Порядок выполнение работы
- •Контрольные вопросы
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Рекомендуемая литература
Порядок выполнения работы
1. Установить термостолбик
так, чтобы втулка на передней панели
термостолбика вошла в отверстие на
переднй панели печи. При этом расстояние
от излучателя с площадью
 до
приёмника с площадью
до
приёмника с площадью
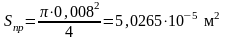 равно
равно
 м.
м.
2. Включить устройство
измерительное выключателем СЕТЬ на его
задней панели и дать прогреться в течение
5 мин (при этом на индикаторах
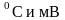 должны
установиться значения 000 и 0,00
соответственно).
должны
установиться значения 000 и 0,00
соответственно).
3. Включить печь с помощью выключателя СЕТЬ ( при этом ручка «СКОРОСТЬ НАГРЕВА» должна находиться в положении MIN), а для исключения перегрева корпуса печи включите с помощью выключателя ВЕНТ. вентилятор охлаждения. Крутя ручку «СКОРОСТЬ НАГРЕВА» добейтесь того, чтобы печь начала нагреваться.
4. Постепенно нагревая печь
снимите зависимость напряжения
термостолбика от температуры в печи.
Показания напряжения термостолбика
снимать при изменении температуры на
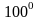 С.
Отсчёты следует производить, когда
напряжение с термостолбика и температура
в печи будут очень медленно меняться.
Поэтому, если нагрев очень быстрый,
перед отсчётом следует уменьшить
скорость нагрева. Данные измерений
занести в таблицу 1.
С.
Отсчёты следует производить, когда
напряжение с термостолбика и температура
в печи будут очень медленно меняться.
Поэтому, если нагрев очень быстрый,
перед отсчётом следует уменьшить
скорость нагрева. Данные измерений
занести в таблицу 1.
Более качественные результаты получаются, когда отсчёт производят во время теплового равновесия печи. При этом показания температуры в печи и показания напряжения с термостолбика не меняются.
5. После достижения максимально заданной температуры печи, поверните ручку регулирования скорости нагрева в положение MIN, выключите выключатель СЕТЬ на передней панели печи, при этом начнётся охлаждение печи (вентилятор должен работать).
6. С помощью калибровочной
таблицы (рис. 7) определить поток (мощность
замещения
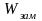 ),
соответствующий полученным значениям
напряжения термостолбика.
),
соответствующий полученным значениям
напряжения термостолбика.
7. Построить в масштабе график зависимости от температуры. Взяв на графике две произвольные точки, определить соответствующие им значения потоков и температур.
8. Произвести расчёт постоянной Больцмана для полученных значений по формуле:
9. Сравнить полученное значение с теоретическим и сделать вывод по проделанной работе.
Таблица 1.
№ п/п |
|
,К |
|
,Вт |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
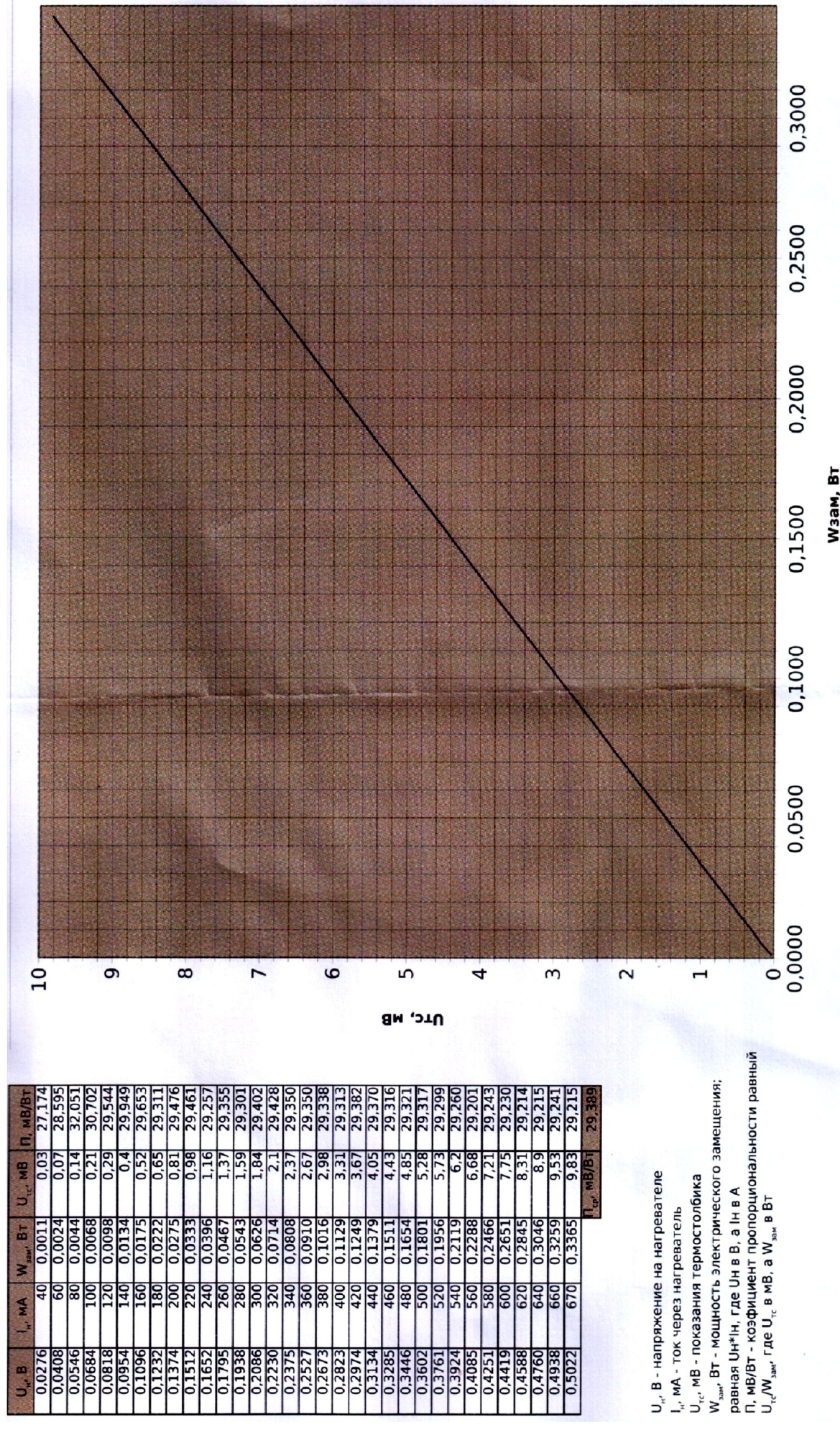
Калибровочная характеристика термостолбика
Рисунок 7.
Контрольные вопросы
1. Дайте определение теплового излучения.
2. Какие величины характеризуют тепловое излучение?
3. Что называется потоком энергии, энергетической светимостью, спектральной плотностью энергетической светимости (испускательной способностью)?
4. Как связаны между собой энергетическая светимость и спектральная плотность энергетической светимости?
5. Что называется абсолютно черным телом? Какова идеальная модель абсолютно черного тела?
6. Сформулируйте и запишите законы теплового излучения абсолютно черного тела:
закон Стефана - Больцмана;
законы Вина;
закон Планка.
7. Объясните методику проверки закона Стефана – Больцмана.
Работа 65. Изучение внешнего фотоэффекта
Цель работы
Работа Б-5. Определение ширины запрещенной зоны полупроводников
Цель работы
Экспериментально исследовать зависимость сопротивления полупроводника от температуры, определить ширину запрещенной зоны (энергию активации) и температурный коэффициент сопротивления полупроводника.
Приборы и принадлежности:
Терморезистор.
Электронагреватель.
Термометр.
Мост сопротивлений.
Источник тока.
ЛАТР.
Соединительные провода.
Краткая теория.
Электрон изолированного атома имеет некоторые определенные значения энергии, которые изображают в виде энергетических уровней. На рис.1 представлены энергетические уровни изолированного атома.
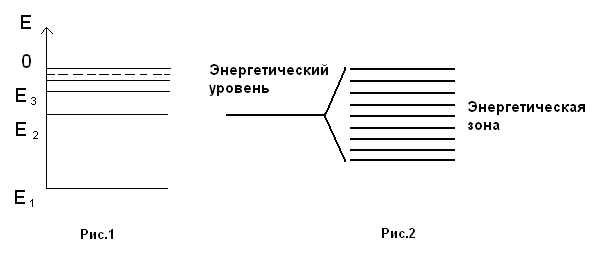
Для образования кристалла будем «мысленно» сближать N изолированных атомов. Взаимодействие электрона со всеми N атомами кристалла приводит к изменению энергии электрона. Каждый энергетический уровень атома расщепляется на N уровней, и образуются энергетические зоны (см. рис.2).
 В
кристалле все энергетические уровни
можно разделить на три энергетические
зоны. Энергетические уровни валентных
электронов атомов образуют валентную
зону (см. рис. 3). Свободные электроны
могут иметь в кристалле не любые, а
дискретные (некоторые определённые)
значения энергии. Энергетические уровни
свободных электронов образуют свободную
зону или зону проводимости.
В
кристалле все энергетические уровни
можно разделить на три энергетические
зоны. Энергетические уровни валентных
электронов атомов образуют валентную
зону (см. рис. 3). Свободные электроны
могут иметь в кристалле не любые, а
дискретные (некоторые определённые)
значения энергии. Энергетические уровни
свободных электронов образуют свободную
зону или зону проводимости.
Свободная зона отделена от валентной зоны запрещенной зоной - полосой энергии, запрещенной для электронов. Величина E называется шириной запрещенной зоны.
При
температуре
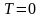 электроны кристалла заполняют нижние
энергетические уровни. По принципу
Паули: на каждом энергетическом уровне
может находиться не более двух электронов
с противоположно направленными спинами.
электроны кристалла заполняют нижние
энергетические уровни. По принципу
Паули: на каждом энергетическом уровне
может находиться не более двух электронов
с противоположно направленными спинами.
У
полупроводников при температуре 0 К
полностью заполнена электронами
валентная зона. В свободной зоне
электронов нет. Ширина запрещенной зоны
полупроводников небольшая:
 порядка 1эВ. С ростом температуры
электроны, получая энергию, могут
переходить на вышележащие энергетические
уровни. Энергии теплового движения
электронов и энергии электрического
поля тока достаточно для перехода
электронов из валентной зоны полупроводника
в зону проводимости.
порядка 1эВ. С ростом температуры
электроны, получая энергию, могут
переходить на вышележащие энергетические
уровни. Энергии теплового движения
электронов и энергии электрического
поля тока достаточно для перехода
электронов из валентной зоны полупроводника
в зону проводимости.
При подключении полупроводника к источнику тока в цепи появляется электрическое поле. Свободные электроны в зоне проводимости под действием этого поля движутся противоположно полю (вектору напряженности электрического поля) и образуют электронную проводимость полупроводника. В валентной зоне на месте ушедшего электрона остаётся некомпенсированный положительный электрический заряд – дырка. Под действием электрического поля электрон с соседнего уровня может перейти на место дырки, там, откуда электрон ушел образуется новая дырка. Можно сказать, что дырки движутся по полю. Дырки в валентной зоне образуют дырочную проводимость полупроводника. Электронная и дырочная проводимости химически чистого полупроводника составляют собственную проводимость полупроводника.
Электрическая проводимость в кристалле пропорциональна концентрации носителей тока (электронов и дырок). Распределение электронов по энергетическим уровням характеризуется функцией Ферми - Дирака
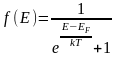 , (1)
, (1)
где Е – энергия электрона, ЕF – энергия Ферми, k = 1,38∙10-23 Дж/К – постоянная Больцмана, Т – абсолютная температура кристалла.
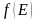 – функция Ферми-Дирака, которая
определяет вероятность нахождения
электрона на энергетическом уровне с
энергией Е .
– функция Ферми-Дирака, которая
определяет вероятность нахождения
электрона на энергетическом уровне с
энергией Е .
При = 1 на энергетическом уровне находятся 2 электрона;
= 0,5 на энергетическом уровне находится 1 электрон;
= 0 на энергетическом уровне электронов нет.
В металле энергией Ферми называют максимальную кинетическую энергию, которую могут иметь электроны проводимости при температуре 0 К. Энергетический уровень, соответствующий энергии Ферми, называется уровнем Ферми. Таким образом, уровень Ферми – это верхний заполненный электронами энергетический уровень в металле при температуре 0 К.
Значение уровня Ферми в химически чистом полупроводнике, отсчитанное от потолка валентной зоны, приблизительно равно половине ширины запрещенной зоны
 .
(2)
.
(2)
Отсюда следует что, уровень Ферми находится посередине запрещенной зоны. Если энергия электрона, находящегося в зоне проводимости, равна Е, тогда из рис.3 видно, что
 (3)
(3)
При невысоких температурах в формуле (1) единицей в знаменателе можно пренебречь. Учитывая выражение (3), из формулы (1) получают
 . (4)
. (4)
Удельная
проводимость полупроводника
 пропорциональна концентрации носителей
тока, поэтому она пропорциональна
функции Ферми – Дирака (формула (4)),
тогда можно записать
пропорциональна концентрации носителей
тока, поэтому она пропорциональна
функции Ферми – Дирака (формула (4)),
тогда можно записать
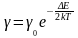 ,
,
где
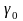 –
постоянная величина, зависящая от
данного полупроводника. Сопротивление
обратно пропорционально проводимости,
поэтому его можно представить в виде
–
постоянная величина, зависящая от
данного полупроводника. Сопротивление
обратно пропорционально проводимости,
поэтому его можно представить в виде
 , (5)
, (5)
Здесь А – коэффициент, зависящий от физических свойств полупроводника. Из формулы (5) видно, что с ростом температуры сопротивление полупроводника R уменьшается. По зонной теории эта закономерность объясняется следующим образом: при увеличении температуры растет число электронов в свободной зоне и число дырок в валентной зоне, поэтому проводимость полупроводника увеличивается, а сопротивление уменьшается. У металлов с ростом температуры сопротивление увеличивается.
Для
определения ширины запрещенной зоны
 необходимо прологарифмировать формулу
(5)
необходимо прологарифмировать формулу
(5)
 (6)
(6)
Коэффициент А неизвестен, поэтому сначала записывают формулу (6) для двух разных температур Т1 и Т2
 , (7)
, (7)
 . (8)
. (8)
Вычитают из формулы (7) выражение (8)
 . (9)
. (9)
Из формулы (9) для ширины запрещенной зоны получают расчетную формулу
 (10)
(10)
Г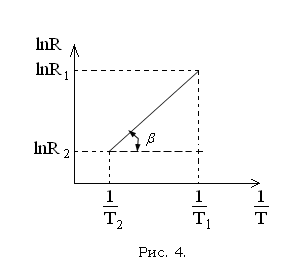 рафик
зависимости
рафик
зависимости
 lnR
от 1/T для полупроводника
с собственной проводимостью представляет
собой прямую линию (рис. 4), тангенс угла
наклона которой к оси абсцисс равен
lnR
от 1/T для полупроводника
с собственной проводимостью представляет
собой прямую линию (рис. 4), тангенс угла
наклона которой к оси абсцисс равен
 . (11)
. (11)
Сравнивая формулы (10) и (11), можно получить

Температурный
коэффициент сопротивления
 показывает относительное изменение
сопротивления при нагревании вещества
на 1 К
показывает относительное изменение
сопротивления при нагревании вещества
на 1 К
 . (12)
. (12)
Единица
измерения в СИ
 .
.
Взяв производную сопротивления по температуре в формуле (5), можно записать:
 (13)
(13)
Формулу (13) подставляют в формулу (12) и, учитывая формулу сопротивления R (5), получают
 .
.
Расчетная формула для температурного коэффициента сопротивления полупроводника равна
 . (14)
. (14)
Температурный коэффициент сопротивления полупроводников зависит от температуры и химической природы вещества. Знак минус в формуле (14) учитывает, что с ростом температуры сопротивление полупроводника уменьшается. У металлов температурный коэффициент сопротивления является положительной величиной.

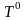 С
С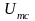 ,мВ
,мВ