Примеры

• «пропылесосить ковер» требует время, линейно зависящее от его площади (O(A)), то есть на ковер, площадь которого больше в два раза, уйдет в два раза больше времени. Соответственно, при увеличении площади ковра в сто тысяч раз, объем работы увеличивается строго пропорционально в сто тысяч раз, и т. п.

• «найти имя в телефонной книге» требует всего лишь время, логарифмически зависящее от количества записей (O(log₂(n))), так как, открыв книгу примерно в середине, мы уменьшаем размер «оставшейся проблемы» вдвое (за счет сортировки имен по алфавиту). Таким образом, в книге, толщиной в 1000 страниц, любое имя находится не больше чем за log₂1000≈10 раз (открываний книги). При увеличении объема страниц до ста тысяч, проблема все еще решается за log₂100000≈17 заходов.

Правила для определения сложности

1. O(k*f) = O(f)

2. O(f*g) = O(f)*O(g) или O(f/g) = O(f)/O(g)

3. O(f+g) равна доминанте O(f) и O(g)

Здесь k обозначает константу, a f и g - функции.

Первое правило, приведенное выше, декларирует, что постоянные множители не имеют значения для определения порядка сложности:

1,5*N=O(N)

Из второго правила следует, что порядок сложности произведения двух функций равен произведению их сложностей:

О((17*N)*N)=O(17*N)*O(N)=O(N)*O(N)=O(N*N)=O(N²)

Из третьего правила следует, что порядок сложности суммы функций определяется как порядок доминанты первого и второго слагаемых, т.е. выбирается наибольший порядок:

О(N⁵+N²)=O(N⁵)

O-сложность алгоритмов.

O(1): Большинство операций в программе выполняются только раз или только несколько раз алгоритмами константной сложности. Любой алгоритм, всегда требующий независимо от размера данных одного и того же времени, имеет константную сложность.

О(N): Время работы программы линейно, когда каждый элемент входных данных требуется обработать лишь линейное число раз.

О(N²),О(N³),О(N^α): Полиномиальная сложность. О(N²) - квадратичная сложность, О(N³) - кубическая сложность

О(Log(N)): Когда время работы программы логарифмическое, программа начинает работать намного медленнее с увеличением N. Такое время работы встречается обычно в программах, которые делят большую проблему в маленькие и решают их по отдельности.

O(N*log(N)): Такое время работы имеют те алгоритмы, которые делят большую проблему в маленькие, а затем, решив их, соединяют их решения.

O(2^N): Экспоненциальная сложность. Такие алгоритмы чаще всего возникают в результате подхода именуемого метод грубой силы.

Программист должен уметь проводить анализ алгоритмов и определять их сложность. Временная сложность алгоритма может быть посчитана исходя из анализа его управляющих структур.

Реализация алгоритмических конструкций в С#

Следование

Алгоритмическая конструкция «следование» на блок-схеме изображается в виде нескольких блоков, обычно расположенных один под другим, управление которым передается сверху вниз:

На псевдокоде та же самая последо­вательность операций запишется следующим образом:

Начало

Ввод А и В

С = А + В

Вывод С

Конец

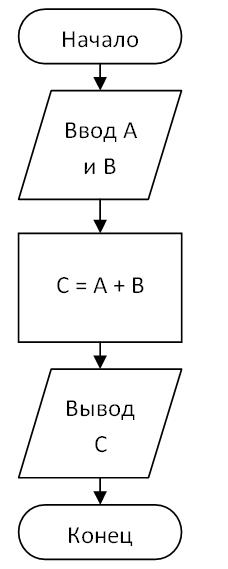
Для реализации в языке программирования алгоритмической структуры «следование» никаких специальных ключевых слов не требуется. Любая последовательность операторов, записанных друг за другом, будет выполняться также последовательно в том же самом порядке.

Любая программа, использованная в предыдущем разделе нашего курса, реализует именно эту алгоритмическую структуру. Например, программа, иллюстрирующая работу побитовых операторов:

using System;

namespace Bitwise

{

class BitWiseApp

{

static void Main(string[] args)

{

uint op = 0x5A5A;

uint result = op & 0xA;

System.Console.WriteLine("op = {0:X}, op & 0xA = {1:X}",

op, result);

result = op | 0xF;

System.Console.WriteLine("op = {0:X}, op | 0xF = {1:X}",

op, result);

result = op ^ 0xF;

System.Console.WriteLine("op = {0:X}, op ^ 0xF = {1:X}",

op, result);

result = ~op;

System.Console.WriteLine("op = {0:X}, ~op = {1:X}",

op, result);

result = op << 3;

System.Console.WriteLine("op = {0:X}, op << 3 = {1:X}",

op, result);

result = op >> 3;

System.Console.WriteLine("op = {0:X}, op >> 3 = {1:X}",

op, result);

System.Console.ReadLine();

}

}

}

В данной программе использовано четырнадцать операторов, и все они выполняются строго друг за другом.

Ветвление

Ветвление в алгоритме предполагает выбор одного из нескольких возможных путей выполнения программы. Обычно в языках программирования ветвление реализуется с использованием условного оператора if. С помощью этого программа может проверить выполнение некоторого условия и на основании результатов проверки принять решение о выполнении того или иного фрагмента кода.

Обычно условные операторы разделяют на простые и вложенные. Кроме того, существует сокращенная запись условного оператора, используемая в том случае, когда полная запись не является необходимой.

Ветвление и условный оператор

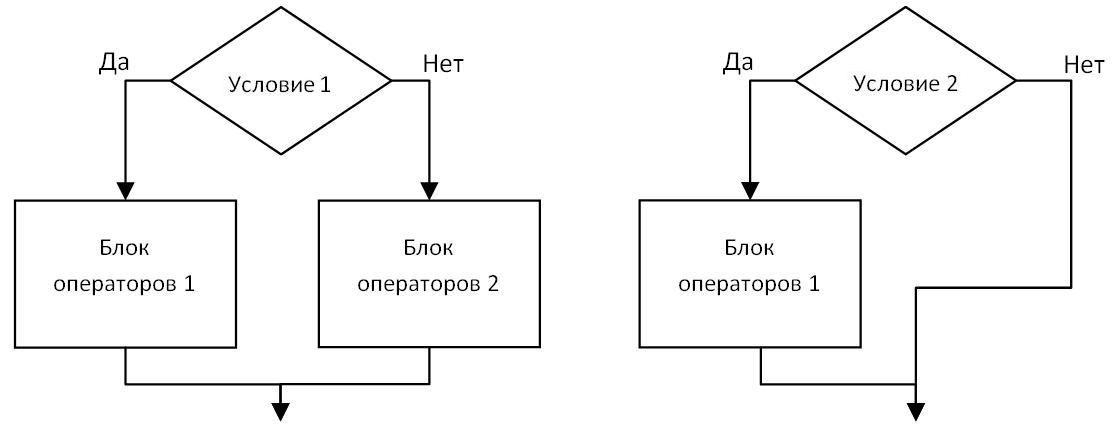
Ветвление на блок-схеме алгоритма изображается в двух вариантах:

На псевдокоде первый вариант этой конструкции имеет вид:

Если <Условие> То

Блок Операторов 1

Иначе

Блок Операторов 2

Все-Если

Действует эта конструкция следующим образом. Если <Условие>, записанное после Если, истинно, выполняется <Блок Операторов 1>. В противном случае управление передается <Блоку Операторов 2>.

Второй вариант ветвления используется, если при ложности условия не нужно выполнять никаких действий. В этом случае управление передается блоку, расположенному после завершения <Блока Операторов 1>.

На псевдокоде этот вариант выглядит так:

Если <Условие> То

Блок Операторов 1

Все-Если

В программе на C# ветвление реализуется с помощью условного оператора if, который в общем виде выглядит следующим образом:

if(<Выражение>)

<Оператор 1>

[else

<Оператор 2>]

Логическое выражение в скобках вычисляется при выполнении оператора и может иметь значения true или false. В зависимости от значения этого выражения выполняется либо <Оператор 1>, либо <Оператор 2>. Оператор if может содержать необязательную конструкцию else. Так как эта конструкция необязательная, то при описании синтаксиса оператора она заключается в квадратные скобки.

Если конструкция else отсутствует и выражение в скобках равно false, то <Оператор 1> просто пропускается и выполняется следующий после него оператор.

Приведем простой пример:

int i = 2;

int j = 3;

if(i > j)

System.Console.WriteLine("{0} > {1}", i, j );

else

System.Console.WriteLine("{0} < {1}", i, j);

В этом примере для записи выражения в скобках (то есть условия) мы использовали оператор отношения > (больше). Если содержимое переменной i больше содержимого переменной j, то выполняется строка, расположенная сразу после оператора if, а если меньше или равно, то строка, расположенная сразу после оператора else.

В результате работы этого фрагмента программы на консоли будет отображено правильное неравенство 2 < 3.

В предыдущем примере в зависимости от результата проверки условия мы выполняли одно из двух выражений, ограниченных символом точка с запятой. Если нужно выполнять не одно, а несколько таких выражений, следует использовать фигурные скобки. В этом случае говорят о блоке операторов, который выполняется, если условие истинно:

int i = 2;

int j = 3 ;

if (i != 0)

{

float x = (float) j / i;

System.Console.WriteLine("{0} / {1} = {2}", j, i, x);

}

Здесь мы заключили в фигурные скобки две строки программы с выражениями, которые должны выполняться, если переменная i не равна нулю.

В первой строке данного фрагмента программы выполняется деление переменной j на переменную i, результат записывается в переменную х. Обратите внимание, что перед делением тип переменной j явным образом преобразуется из целого числа в число с плавающей запятой. Если этого не сделать, в результате целочисленного деления пропадет остаток от деления.

Вложенные условия

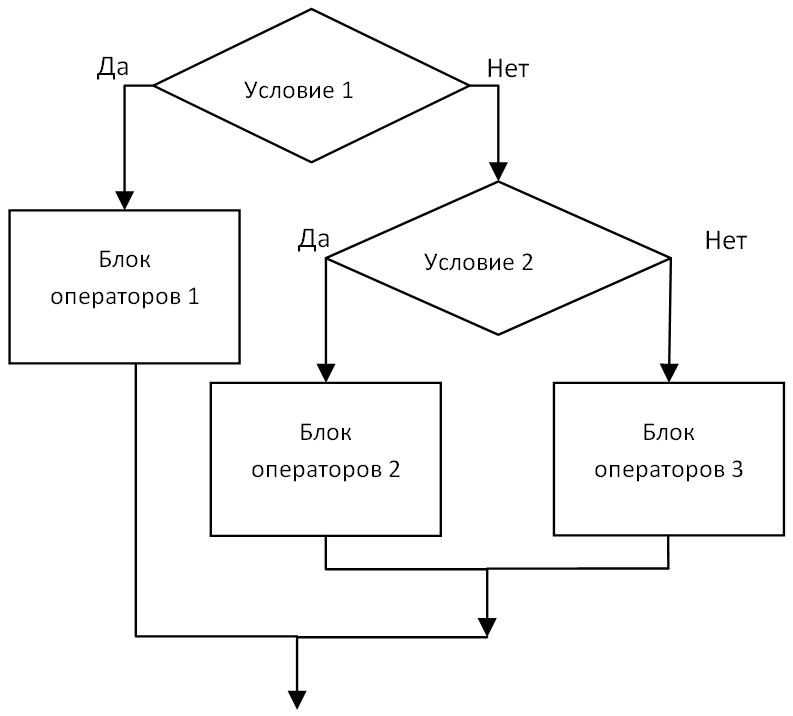
В любом блоке операторов, используемом в конструкции ветвления, может также использоваться ветвление. В этом случае эти конструкции называются вложенными:

На псевдокоде вложенные условия выглядят так:

Если <Условие 1> То

Блок Операторов 1

Иначе

Если <Условие 2> То

Блок Операторов 2

Иначе

Блок Операторов 3

Все-Если

Все-Если

Конструкции ветвления и, соответственно, условные операторы допускается вкладывать друг в друга без ограничений. В результате можно проверять довольно сложные условия.

Рассмотрим, например, следующий фрагмент программы:

int i = 2 ;

int j = 3 ;

if(( i - j) * 2 > 0)

System.Console.WriteLine("({0} - {1}) * 2 > 0", i, j);

else

{

System.Console.WriteLine("({0} - {1}) * 2 <= 0", i, j);

bool f;

f = (i == i);

if(f)

{

System.Console.WriteLine("i == i");

}

}

Здесь мы вначале проверяем значение выражения (i - j) * 2 > 0. Учитывая инициализацию переменных i и j , это выражение должно быть ложно, т. е. равно false. Далее в дело включается конструкция else.

В зависимости от знака выражения на консоли отображается одна из двух строк. В нашем случае выражение имеет отрицательный знак (оно равно -2), поэтому на консоль будет выведено.

(2 - 3) * 2 <= 0

Второй оператор if выполняется только в том случае, если выражение (i - j) * 2 меньше или равно нулю. В этом операторе анализируется содержимое логической переменной f. Если эта переменная равна true, то на консоль выводится текстовая строка, показанная ниже:

i == i

Переменная f вычисляется следующим образом:

f = (i == i);

Здесь в переменную f записывается результат операции сравнения переменной i с самой собой. Он всегда равен true.

Вы можете испытать описанные выше приемы использования простых и вложенных условных операторов на программе, исходный текст которой приведен ниже:

using System;

namespace IfElse

{

class IfElseApp

{

static void Main(string[] args)

{

int i = 2;

int j = 3;

if(i > j)

System.Console.WriteLine("{0} > {1}", i, j);

else

System.Console.WriteLine("{0} < {1}", i, j);

if(i != 0)

{

float x = (float) j / i;

System.Console.WriteLine("{0} / {1} = {2}", i, j, x);

}

if((i - j) * 2 > 0)

System.Console.WriteLine("({0} - {1}) * 2 > 0", i, j);

else

{

System.Console.WriteLine("({0} - {1}) * 2 <= 0",i, j);

bool f;

f = (i == i );

if(f)

{

System.Console.WriteLine("i == i");

}

}

System.Console.ReadLine();

}

}

}

В данном здесь виде программа должна выдать следующий результат:

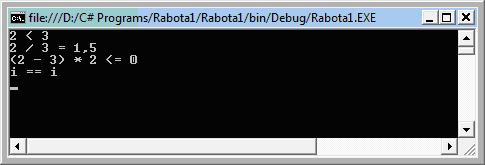
Можете использовать эту программу для собственных экспериментов. Попытайтесь, например, изменить начальные значения переменных, а также логические операторы, заданные в качестве выражений для оператора if.