3.2. Правила построения сетевых графиков

При построении сетевого графика необходимо соблюдать ряд правил.

1. В сетевой модели не должно быть «тупиковых» событий, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события.

2. В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.

3. В сети не должно быть замкнутых контуров и петель, то есть путей, соединяющих некоторые события с ними же самими.

4. Любые два события должны быть непосредственно связаны не более чем одной работой.

5. В сети рекомендуется иметь одно исходное и одно завершающее событие.

6. Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелка завершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.

Простой метод упорядочения сетевого графика основан на понятии ранга события:

• все события сетевого графика подразделяются на ранги,

• к одному рангу может относиться несколько событий,

• нумерация событий производится в соответствии с принадлежностью к тому или иному рангу,

• чем выше ранг, тем больший номер имеет событие,

• внутри одного ранга нумерация событий произвольная.

Начальное событие относим к нулевому рангу и перечеркиваем одной чертой все работы, выходящие из этого события. К первому рангу относим те события, которые не имеют входящих неперечеркнутых стрелок. Далее перечеркиваем двумя чертами работы, выходящие из событий первого ранга. Ко второму рангу относим те события, которые не имеют входящих неперечеркнутых стрелок и т.д.

3.3. Временные параметры сетевых графиков

Параметры событий:

• ранний (ожидаемый) срок t_p(i) свершения i-го события определяется продолжительностью максимального пути, предшествующего этому событию: ;

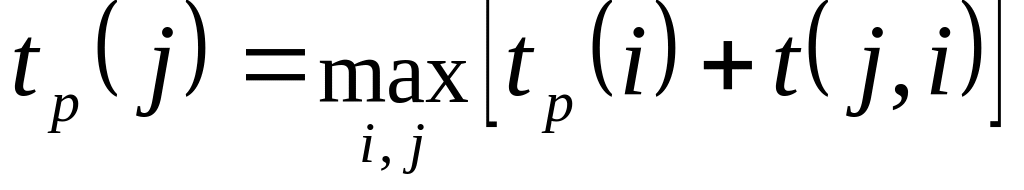• поздний (предельный) срок t_п(i) свершения i-го события равен: ;

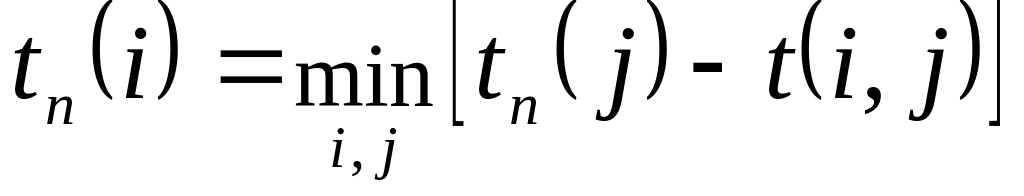• резерв времени R(i) i-го события определяется как разность между поздним и ранним сроками его свершения: .

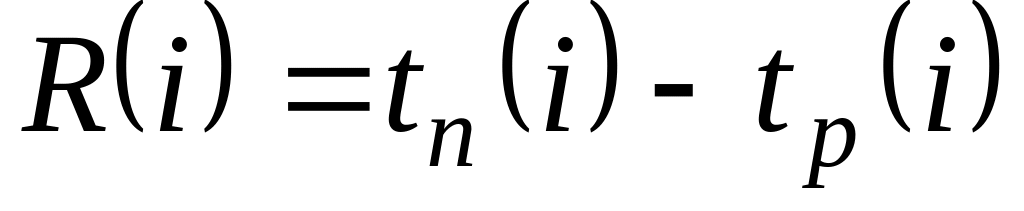Резерв времени показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ. Ранний срок наступления завершающего события сети равен длине критического пути. Критические события резервов времени не имеют. События с нулевыми резервами времени определяют топологию критического пути.

Параметры работ:

• ранний срок t_рн(i,j) начала работы (i,j) совпадает с ранним сроком наступления начального (предшествующего) события i :

;

• ранний срок t_ро(i,j) окончания работы (i,j) определяется по формуле:

;

• поздний срок t_по(i,j) окончания работы (i,j) совпадает с поздним сроком конечного события:

;

• поздний срок t_пн(i,j) начала работы (i,j) определяется по формуле:

.

Резерв времени пути R(L) определяется как разность между длиной критического и рассматриваемого пути: R(L)=t_кр – t(L).

Полный резерв времени R_п (i,j) работы (i,j) показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится:

R_п(i,j) = t_п(j) – t_p(i) – t(i,j).

• Важно помнить. Работы, лежащие на критическом пути, резервов не имеют.

Пример решения задачи. Для заданного сетевого графика рассчитать все параметры событий и работ, определить критический путь и его длину.

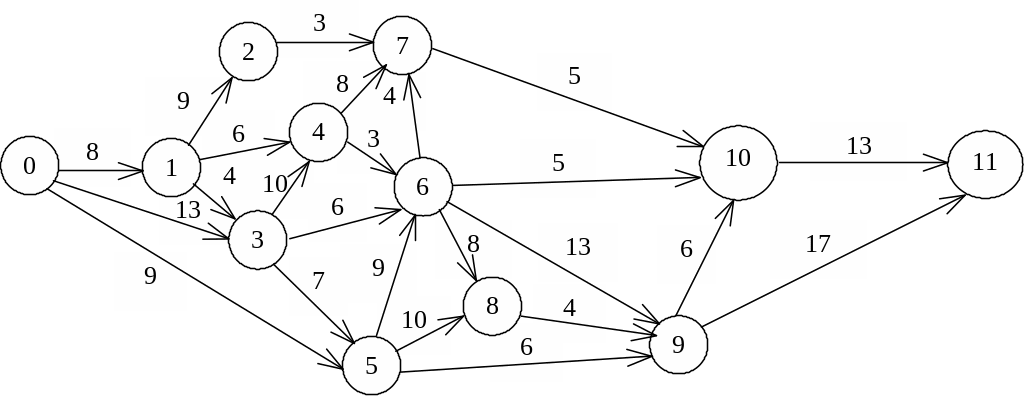
Рис. 3.2. Сетевой график

Расчет временных параметров событий удобно представить в таблице.

Таблица 3.1

Параметры событий сетевого графика

Номер события	0	1	2	3	4	5	6	7	8	9	10	11
Ранний срок tр(i)	0	8	17	13	23	20	29	33	37	42	48	61
Поздний срок tп(i)	0	9	40	13	26	20	29	43	38	42	48	61
Резерв времени R(i)	0	1	23	0	3	0	0	10	1	0	0	0

Критический путь образуют следующие события:

. Топологию критического пути определяют события, резерв времени которых равен нулю. Его продолжительность составляет 61 день (ранний срок свершения последнего события).

Для определения временных параметров работ также используем таблицу, в которую сведем результаты вычислений. Расчеты проводим с помощью приведенных выше формул.

Таблица 3.2

Параметры работ сетевого графика

№	Работа (i,j)	Продолжитель-ность работы (i,j)	Сроки начала и окончания работы				Резерв времени Rп(i,j)
			tрн(i,j)	tро(i,j)	tпн(i,j)	tпо(i,j)
1	(0, 1)	8	0	8	1	9	1
2	(0, 3)	13	0	13	0	13	0
3	(0, 5)	9	0	9	11	20	11
4	(1, 2)	9	8	17	31	40	23
5	(1, 4)	6	8	14	20	26	12
6	(1, 3)	4	8	12	9	13	1
7	(2, 7)	3	17	20	40	43	23
8	(3, 4)	10	13	23	16	26	3
9	(3, 5)	7	13	20	13	20	0
10	(3, 6)	6	13	19	23	29	10
11	(4, 7)	8	23	31	35	43	12
12	(4, 6)	3	23	26	26	29	3
13	(5, 6)	9	20	29	20	29	0
14	(5, 8)	10	20	30	28	38	8
15	(5, 9)	6	20	26	36	42	16
16	(6, 7)	4	29	33	39	43	10
				Продолжение таблицы 3.2
17	(6, 10)	5	29	34	43	48	14
18	(6, 9)	13	29	42	29	42	0
19	(6, 8)	8	29	37	30	38	1
20	(7, 10)	5	33	38	43	48	10
21	(8, 9)	4	37	41	38	42	1
22	(9, 10)	6	42	48	42	48	0
23	(9, 11)	17	42	59	44	61	2
24	(10, 11)	13	48	61	48	61	0