Лабораторная работа №8

Задача 8.14: В транспортном узле имеется запасы 5 типов грузов, также 2 пункта назначения с заявками на 5 типов грузов. Грузы доставляются в пункты назначения 3 видами транспорта с суммарным тоннажем 98, 84 и 88 т. соответственно. Заданы себестоимости перевозки каждого типа груза в каждый пункт назначения каждым видом транспорта (руб/т).

Bi/j		Грузы
		1	2	3	4	5
Пункты назначения	1	30	28	25	26	27
	2	27	25	24	26	30

Ci/j/k		Грузы Ci/j/1					Грузы Ci/j/2						Грузы Ci/j/3
		1	2	3	4	5		1	2	3	4	5		1	2	3	4	5
Пункты назначения	1	63	65	67	69	71		77	79	82	84	87		95	97	101	104	108
	2	83	85	87	89	91		103	105	108	110	113		129	131	135	138	142

Выбрать такое распределение груза по видам подвижного состава, чтобы все грузы были доставлены, а общая стоимость перевозки была минимальна. Выписать целевую функцию и ограничения. Определить суммарную стоимость работ.

Решение

Переменные для описания задачи:

K = 3 – количество видов транспортных среддств;

I = 5 – количество типов грузов;

J = 2 – количество пунктов назначения;

– запас груза в i-го типа в пункте отправления, т, i = 1…5;

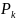– max тоннаж ТС k-го вида, т, k = 1…3;

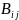– заявка на груз i-го типа j-го пункта назначения, т, i = 1…5, j=1…2;

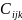– себестоимость перевозки единицы груза i-го типа в j-ый пункт назначения ТС k-го типа, ден.ед., i = 1…5, j = 1…2, k = 1…3;

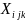– количество груза i-го типа, перевезенного в j-ый пункт назначения транспортным средством k-го типа, т., k=1…3, i=1…5, j=1…2;

Значение переменных , ,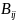 , заданы и входят в состав исходных данных; проектные переменные 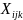определяются в ходе решения задачи линейного программирования.

Целевая функция (суммарный грузооборот) записывается следующим образом:

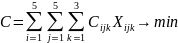(8.1)

Условия:

1. суммарное количество заявок на груз i-го типа во всех пунктах назначения, должно быть не больше количества груза этого типа, имеющегося в пункте отправления:

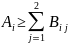(8.2)

2. суммарный тоннаж всех транспортных средств, должен быть не меньше суммарного количество груза, который перевозится этими транспортными средствами:

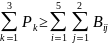(8.3)

Ограничения:

1. суммарное количество груза i-го типа, доставляемый в j-ый пункт назначения всеми видами транспорта, должно быть равно заявкам этих пунктов:

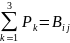, i = 1…5, j = 1…2; (8.4)

2. суммарное количество грузов всех типов, доставляемых в каждый пункт назначения k-м видом транспортного средства, должно быть не больше max тоннажа данного транспортного средства :

, k = 1…3; (8.5)

3. суммарное количество груза i-го типа, доставляющееся во все пункты назначения, всеми видами транспортных средств, должно быть не больше запаса этого груза в пункте отправления :

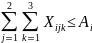, i = 1…5; (8.6)

Сформулированная задача является многопараметрической задачей линейного программирования минимизации критерия (8.1) с учетом выполнения условия (8.2) и (8.3), и ограничений (8.4), (8.5) и (8.6).

Проверим выполнение условия (8.2) и (8.3) решения задачи.

1. Суммарной количество груза, которое имеется во всех пунктах отправления:

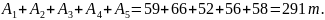
Суммарной количество груза, которое должно быть доставлено во все пункты назначения:

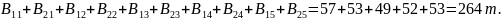
Условие (8.2) выполняется: суммарное количество груза, которое может быть доставлено, превышает суммарное количество груза, которое необходимо доставить на 291 – 264 = 13 т.

2. Суммарное количество груза, которое может быть перевезено каждым видом транспорта:

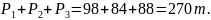
Суммарной количество груза, которое должно быть доставлено во все пункты назначения:

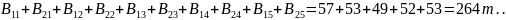
Условие (8.3) выполняется: суммарное количество груза, которое может быть перевезено, превышает суммарное количество груза, которое должно быть доставлено на 270 – 264 = 14 т.

Целевая функция (8.1) записывается следующим образом:

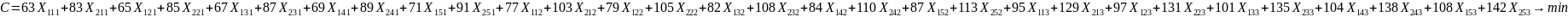
Ограничения (8.4) на доставку груза в пункты назначения записывается следующим образом:

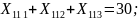
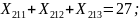
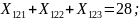
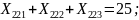
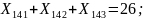
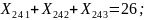
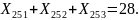
Ограничения (8.5) на суммарное количество груза перевозимого транспортными средствами:

;

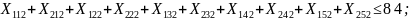
Ограничения (8.6) на суммарное количество груза, перевозимого из пункта отправления:

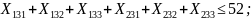
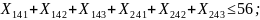
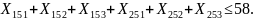
Решение задачи целочисленного линейного программирования осуществляется с использованием средства “Поиска решения” пакета MS Excel методом “ветвей и границ”.

Значение переменных (т), полученные в результате решения задачи, приведены в таблице.

Xi/j/k		Грузы 1					Грузы 2						Грузы 3
		1	2	3	4	5		1	2	3	4	5		1	2	3	4	5
Пункты назначения	1	63	65	67	69	71		77	79	82	84	87		95	97	101	104	108
	2	83	85	87	89	91		103	105	108	110	113		129	131	135	138	142

Значение целевой функции составило 528 ден.ед.

В первый пункт назначения груз доставляется первым типом подвижного состава (124т.), вторым типом (12т.), третьим типом (14т.), во второй пункт – первым типом (186т.), третьим типом (14т.), в третий пункт – первым типом (186т.), вторым типом (60т.), третьим типом (7т.), в четвертый пункт – первым типом (310 т.).