Лабораторная работа №3

Задача 3.14: В 4 пункта назначения доставляется однородный груз 400, 350, 300 и 200 т при этом используется 3 виды подвижного состава с суммарным тоннажем 300, 400 и 600 т. Заданы стоимости доставки единицы груза каждым видом подвижного состава в каждый пункт назначения:

Ci/j		Пункты назначения
		1	2	3	4
Типы ПС	1	100	70	80	180
	2	140	90	90	190
	3	240	110	150	210

Выбрать такое распределение тоннажа подвижного состава по пунктам назначения, чтобы все грузы были доставлены, а общая стоимость перевозки была минимальна. Выписать целевую функцию и ограничения. Определить суммарную стоимость работ.

Решение

Переменные для описания задачи:

I = 3 – количество видов подвижного состава;

J = 4 – количество пунктов назначения;

– суммарный тоннаж подвижного состава, i-го типа, т, i = 1…3;

– суммарный объем перевозок в j-ый пункт назначения, т, j=1…4;

– стоимость доставки единицы груза подвижным составом i-го типа в j-ый пункт назначения, ден.ед., i=1…3, j=1…4;

- количество груза доставляемого i-м типом подвижного состава в j-ый пункт назначения, т., i=1…3, j=1…4.

Значение переменных , , заданы и входят в состав исходных данных; проектные переменные определяется в ходе решения задачи линейного программирования.

Целевая функция (суммарный грузооборот автотранспорта) записывается следующим образом:

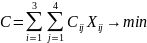(3.1)

Суммарной количество груза, которое необходимо доставить, должно быть не больше суммарного количества груза, которое может быть перевезено. Необходимое условие решения данной задачи:

(3.2)

Ограничения:

1. общее количество груза, доставляемого в j-ый пункт назначения, должно быть равно заявке этого пункта:

, j = 1…4; (3.3)

2. суммарное количество груза доставляемого i-ым типом подвижного состава, не должно превышать суммарного тоннажа этого подвижного состава:

, i = 1…3 (3.4)

Сформулированная задача является многопараметрической задачей линейного программирования минимизации критерия (3.1) с учетом выполнения условия (3.2) и ограничений (3.3) и (3.4).

Проверим выполнение условия (3.2) решения задачи.

Суммарный тоннаж подвижного состава:

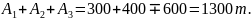
Суммарное количество груза, которое необходимо доставить:

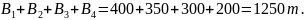
Условие (3.2) выполняется: суммарное количество груза, которое может быть доставлено, превышает суммарное количество груза, которое необходимо доставить на 1300 – 1250 = 50 т.

Целевая функция (3.1) записывается следующим образом:

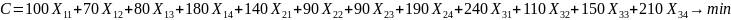
Ограничения (3.3) на доставку груза в пункты назначения записывается следующим образом:

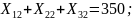
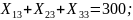
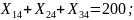
Ограничения (3.4) на суммарный тоннаж груза, доставляемого всеми типами подвижного состава, записывается следующим образом:

;

;

.

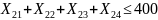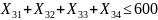Решение задачи целочисленного линейного программирования осуществляется с использованием средства “Поиска решения” пакета MS Excel методом “ветвей и границ”.

Значение переменных (т), полученные в результате решения задачи, приведены в таблице.

Xi/j		Пункты назначения
		1	2	3	4
Типы ПС	1	300	0	0	0
	2	100	0	300	0
	3	0	350	0	200

Значение целевой функции составило 151500 ден.ед.

В первый пункт назначения груз доставляется первым типом (300 т.), вторым типом (100 т.), во второй пункт – третьим типом (350 т.), в третий пункт – вторым типом (300 т.), в четвертый пункт – третьим типом (200 т.).