ФИЛИАЛ ЧОУ ВПО «ЮЖНО-УРАЛЬСКИЙ ИНСТИТУТ УПРАВЛЕНИЯ И ЭКОНОМИКИ»

В Г. ЗЛАТОУСТЕ

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

по выполнению домашней контрольной работы по дисциплине

«ДИСКРЕТНАЯ МАТЕМАТИКА»

Для студентов заочной формы обучения

По направлению:

230201.65 «Информационные системы и технологии»

Златоуст, 2012

Содержание

Введение	3
Методические рекомендации по выполнению контрольных заданий	4
Примеры решения задач	5
Задания для домашней контрольной работы	9
Контрольные вопросы	19
Рекомендуемый список литературы	20
Приложение А. Образец оформления титульного листа	21
Приложение Б. Образец оформления карточки рецензента	22

Введение

Контрольные задания по курсу «Дискретная математика» предназначены для студентов филиала Южно-уральского института экономики и управления в г. Златоусте, обучающихся по заочной форме.

Целью преподавания дисциплины «Дискретная математика» состоит в ознакомлении студентов данного направления с основными понятиями, положениями и методами дискретной математики. Дисциплина «Дискретная математика» формирует базовые знания и кругозор, необходимые для освоения обще-профессиональных и специальных дисциплин.

Контрольная работа посвящена таким разделам дискретной математики как математическая логика и теория алгоритмов. Данные курсы способствуют созданию условий для формирования профессиональных навыков будущего специалиста.

Содержание заданий соответствует минимуму требований Государственного стандарта высшего профессионального образования по специальности 230201.65 «Информационные системы и технологии».

Методические рекомендации по выполнению контрольной работы

1. При выполнении и оформлении контрольной работы необходимо соблюдать следующие правила:

2. Контрольную работу следует оформлять в отдельной тетради чернилами синего или чёрного цвета, оставляя поля для замечаний преподавателя.

3. Материал работы следует располагать в следующей последовательности:

• титульный лист (приложение А);

• карточка рецензента (приложение Б);

• содержание (приложение В);

• практическая часть;

• список используемой литературы.

4. Перед решением каждой задачи необходимо полностью выписать её условие.

5. Решение задачи следует начинать с новой страницы.

6. Решение задачи должно доводиться до ответа, требуемого условием. В промежуточных вычислениях не следует вводить приближённые значения величин.

Контрольная работа представляется на проверку за месяц до начала экзаменационной сессии.

При возврате проверенной, но не зачтенной работы студент должен внести исправления по замечаниям рецензента и сдать работу на повторную проверку.

Контрольные работы с нарушением перечисленных требований на проверку не принимаются.

Работа выполняется по вариантам, которые определяются по последней цифре номера студенческого билета:

Номер студенческого билета	Номер выполняемого варианта
№ 1, 11, 21, 31, 41	Первый
№ 2, 12, 22, 32, 42	Второй
№ 3, 13, 23, 33, 43	Третий
№ 4, 14, 24, 34, 44	Четвертый
№ 5, 15, 25, 35, 45	Пятый
№ 6, 16, 26, 36, 46	Шестой
№ 7, 17, 27, 37, 47	Седьмой
№ 8, 18, 28, 38, 48	Восьмой
№ 9, 19, 29, 39, 49	Девятый
№ 10, 20, 30, 40, 50	Десятый

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1

Выполнить перевод числа 19

а) в двоичную систему счисления;

б) в 16-ю систему счисления.

Перевести полученные числа в десятичную систему счисления

Решение.

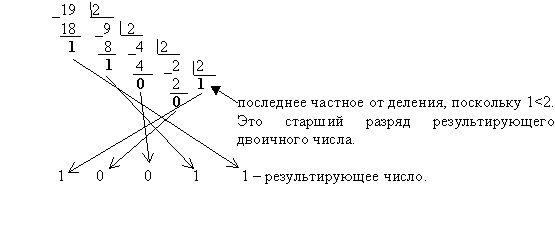
Ответ: а) 19 =10011₂

Решение задачи (б) и переход к десятичной системе счисления смотрите в Лекции № 7 «Системы счисления».

Задача № 2

Даны множества А, В, С. Количество элементов: |A|=19; |B|=17; |C|=22; |A∩B|=10; |A∩C|=12; |B∩C|=11; |A∩B∩C|=8. Всего элементов в U 50. Найти количество элементов в дополнении к объединению всех трех множеств.

Решение. Найдем количество элементов в объединении

19+17+22-(10+12+11)+8=33

Следовательно, количество элементов в дополнении 50-33=17.

Задача № 3

Алексею предлагается на выбор четыре книги из 10 имеющихся в библиотечном фонде, по интересующей его теме. Сколько возможно различных выборов (при условии, что Витя выбирает именно четыре книги)?

Решение. Нас интересует число неупорядоченных наборов 4 из 10 объектов. Это формула числа сочетаний:

Задача № 4

Для графа, изображённого на рисунке определить степени всех вершин графа. Определить расстояния между вершинами, радиусы и центры графа. Задать граф списком вершин и рёбер, матрицей смежности.

1 2

3. 4

Решение. Граф ориентированным не является, так как содержит неориентированные ребра {1,3}, {3,4}, {2,4}, т.е. по данным ребрам можно переходить в обе стороны.

Матрица смежности графа имеет вид

G	1	2	3	4
1	0	1	1	0
2	1	0	1	1
3	1	0	0	1
4	1	1	1	0

Список ребер: {1,3}, {3,4}, {2,4}, (2,1), (1,2), (2,3), (4,1)

1 = 3; 2 = 2; 3 = 3; 4 = 2 (полустепени входа)

1 = 2; 2 = 3; 3 = 2; 4 = 3 (полустепени выхода)

Факторизованная запись

Матрица расстояний 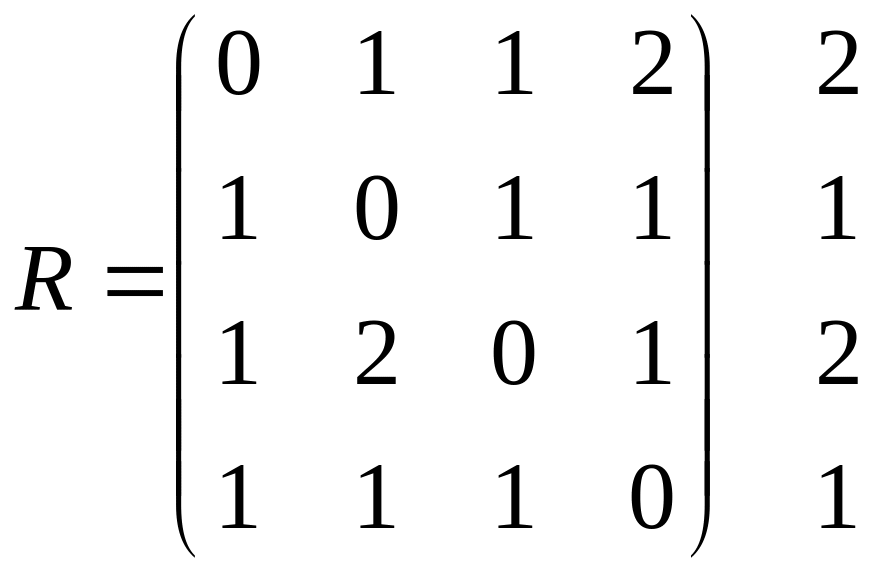r(G)=1, d(G)=2 Центр {2,4}