1. Образование и распространение волн в упругой среде

Если колеблющееся тело находится в упругой среде, то оно приводит в колебательное движение соприкасающийся с ним частицы. Передача колебаний обусловлена силами упругости между частицами, возникающими вследствие деформации среды при ее колебаниях. Явление распространения колебаний в упругой среде называется волновым движением или волной.

Существует много волн различного типа. Одним из видов механических волн являются упругие волны и, в частности, звуковые волны. Огромное значение имеют электромагнитные волны. Однако среди многообразия волновых процессов во всех их видах имеется много общего. При волновом процессе колеблющиеся частицы не перемещаются вместе с волной, они лишь колеблются около своего положения равновесия и передают движение.

Если частицы колеблются вдоль направления распространения волны, то в олна называется продольной если частицы колеблются перпендикулярно распространению волны, то волна называется поперечной. На рис. 27.1 схематично показаны продольная (а) и поперечная (б) волны. В жидкостях и газах силы упругости возникают при деформациях сжатия и растяжении, поэтому в таких средах возникают лишь продольные волны. В твердых телах могут возникать деформации сдвига, поэтому здесь возникают поперечные волны. Скорость распространения волны V будет тем меньше, чем больше плотность среды ρ, и тем больше, чем сильнее связь между частицами или упругие свойства среды. Расчеты дают зависимости:

(27.1) - для продольной волны.

(27.2) - для поперечной волны.

Здесь E - модуль Юнга, G - модуль сдвига*.

*) Модуль Юнга , где α - коэффициент упругости, величина, характеризующая деформацию растяжения или сжатия. При деформации сдвига , где n - коэффициент сдвига (величина аналогичная α).

Поверхность, до которой доходят колебания в данный момент времени, называется фронтом волны. Если фронт-плоскость, то волна плоская, если сфера, то волна сферическая. Простейшим типом волн являются плоские волны. Такая волна распространяется вдоль одного направлениями колебания частиц среды в ней происходят в плоскостях перпендикулярных направлению распространения.

Для построения положения волнового фронта пользуются

п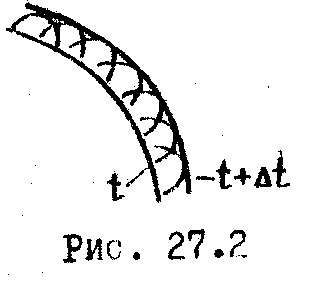 ринципом Гюйгенса: каждая точка фронта волны является источником элементарных вторичных волн. Огибающая всех элементарных волн представляет новый фронт волны (Рис. 27.2). При этом радиус элементарной вторичной волны .

2. Уравнение бегущей волны

Бегущими волнами называют волны, распространяющиеся в не ограниченной среде, где нет отражений.

Пусть в точке среды о координатой x=0 происходит гармоническое к олебание о частотой ω. Смещение точки S от положения равновесия описывается уравнением S=S₀cosωt, где S₀ - амплитуда колебания. Это колебание передается вдоль оси x; со скоростью V. В точку А оно переместится спустя время (Рис. 27.3). Колебательное движение в этой точке будет отставать по фазе от точки x=0 на ωτ и, следовательно, будет описываться соотношением:

(27.3)

Это и есть уравнение бегущей волны. Величина V называется фазовой скоростью. Она характеризует скорость распространения горба или впадины в направлении оси x, т.е. точек волны, колеблющихся в одинаковой фазе. Расстояние, пройденное волной за один период, называют длинной волны λ:

(27.4)