3. Сложение двух перпендикулярных гармонических колебаний

Найдем результирующую траекторию частицы, совершающую гармонические колебания с одинаковой частотой вдоль взаимно перпендикулярных осей x и y по закону: ,

Для нахождения траектории частицы надо из этих выражений исключить время.

Вычисления дают:

(25.22)

Это есть общее уравнение эллипса. Когда , уравнение (25.22) принимает вид:

(25.23)

если a=b , то эллипс превращается в окружность .

П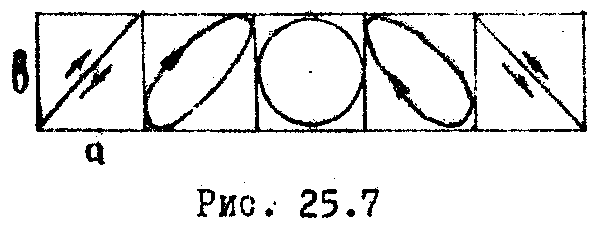 ри , 2π, 4π… (25.22) сводится к прямой:

(25.24)

При , 3π, … получаем также прямую .

Траектории частиц при разных, значениям изображены на рис.25.7. Когда δ=0, π, 2π, эллипс вырождается в прямую, и результирующие колебания происходят в одной плоскости. Такие колебания называют плоско-(или линейно)-п оляризованными. При других значениях δ получают круговую или эллиптическую поляризацию.

Если частоты складываемых колебаний неодинаковы, то результирующее движение становится более сложным. Его называют фигурами Лиссажу (рис. 25.8).

4. Затухающие колебания

В реальных условиях некоторая доля энергии теряется из-за наличия сопротивления или вязкости (механические колебания), или в случае электрических колебаний, некоторая часть запасенной энергии выделяется в виде тепла в проводниках. Составим уравнения таких колебаний, которые называют свободными или

затухающими. В случае механических колебаний наличие сопротивления движению означает действие другой силы, которую полагают пропорциональной скорости:

,

где r - постоянный коэффициент. В этом случае добавление этого слагаемого к уравнению соботвенных колебаний типа (25.4) приводит к выражению:

(26.1)

Это уравнение затухающих механических колебаний.

Для электрических колебаний в контуре при отличном от нуля сопротивлении R согласно закону Кирхгофа U_c+U_R=ε_S или , т.к. , то:

(26.2)

Уравнения (26.1) и (26.2) легко привести к одному виду:

(26.3)

(для электрических колебаний x→q).

Величина β называется коэффициентом затухания, ω₀ - собственная частота. Итак, и механические и электрические затухающие колебания описываются одинаковым уравнением, в котором для механических колебаний:

(26.4)

для электрических колебаний:

(26.5)

Решение такого уравнения будет:

(26.6)

где A₀ и φ₀ - начальные амплитуда и фаза, ω - частота затухающих колебаний р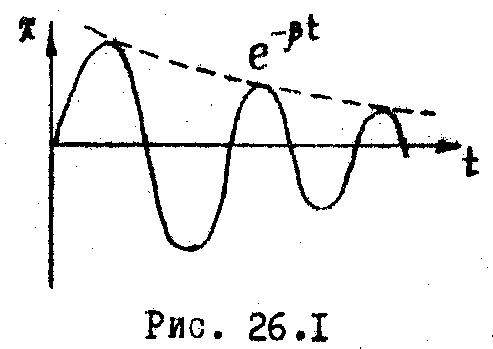 авная:

(26.7)

Как видно, частота затухающих колебаний меньше, чем у свободных, а период - больше. Величина есть амплитуда затухающего колебания, убывающая со временем по экспоненциальному закону (Рис.26.1).

5. Характеристики затухания

Т.к. амплитуда затухающих колебаний убывает со временем по закону , а энергия пропорциональна амплитуде колебаний E~A², то и энергия колеблющейся системы убывает по такому же закону. Поэтому скорость, с которой уменьшается амплитуда и энергия характеризуют экспоненциальным множителем.

Сравнивая между собой значения амплитуд, отличающиеся по времени на период A(t) и A(t+T) видно, что:

для данного колебания. Величина:

(26.8)

называется логарифмическим дескрементом затухания. Она характеризует скорость уменьшения амплитуды.

Затухание можно характеризовать также временем τ, за которое амплитуда уменьшается в e раз, т.е. до величины e^-1=0,368 от ее начального значения A₀. Такое время называют постоянной времени затухания. В момент времени τ достигается амплитуда:

т.е. (26.9)

Сравнивая это выражение с (26.8), находим, что , где N_e - число колебаний, за которое амплитуда уменьшается в e раз. Для характеристики скорости уменьшения, энергии пользуются добротностью колебательном системы Q:

(26.10)

Вычислим для примера добротность колебательного контура. Энергия колебаний , выделение тепла за период равно . Поэтому . Обычно в колебательном контуре затухание мало: . Поэтому:

и

Добротности важнейших колебательные систем, описываемых уравнений тина (26.3) имеют следующий порядок величин:

обычный колебательный контур (на радиочастотах) . . . 10²

камертон . . . 10⁴

электрон в атоме . . . 10⁷