4. Полная система уравнений Максвелла

Как говорилось, уравнения Максвелла не выводятся и являются обобщением опытных фактов: первое - закон электромагнитной индукции, второе - закон полного тока. К ним еще добавляют теорема Гаусса для электрического поля, которая выражает условие незамкнутости электрических силовых линий (существование электрических зарядов), теорему Гаусса для магнитного поля (магнитных зарядов нет), закон Ома и связь и , и . Итак, полная система уравнений имеет вид:

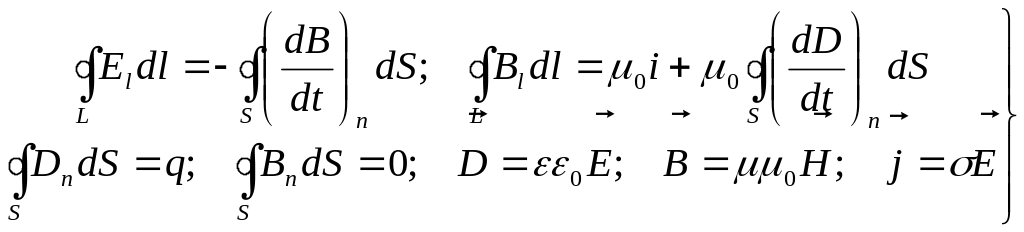(24.7)

физическая сущность уравнений Максвелла сводится к следующему.

Разделение электромагнитного поля на электрическое и магнитное имеет лишь относительный смысл. Если с точки зрения одной инерциальной системы отсчета существует лишь магнитное поле, то с точки зрения другой специальной системы отсчета, движущейся относительно первой со скоростью V, наряду с магнитным полем существует и электрическое. Уравнения Максвелла позволяют решать основную задачу электродинамики: по заданным распределениям зарядов и токов находить и

Лекция 34	Колебательный контур, свободные незатухающие и затухающие колебания, апериодический процесс. Сложение гармонических колебаний одного направления и частоты. Биения.
	Сложение взаимно-перпендикулярных колебаний. Вынужденные электромагнитные колебания, резонанс.

1. Гармонические колебания в электрической системе.

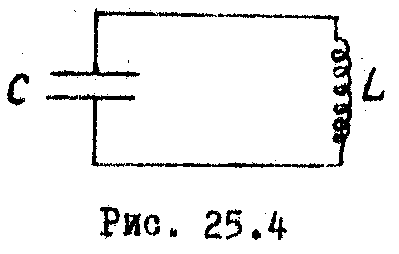Простейшей системой, в которой могут возбуждаться электрические колебания, является замкнутая цепь, состоящая из конденсатора емкостью С и катушки с индуктивностью L (Рис. 25.4). Ее называют колебательным контуром. Если сопротивление равно нулю, то энергия такой электрической системы остается постоянной, и происходит лишь переход энергии электрического поля, запасенной между обкладками конденсатора в энергию магнитного поля, запасенную в катушке, и наоборот. В произвольный момент времени напряжение на катушке индуктивности определяется э.д.с. самоиндукции, вследствие меняющегося тока, текущего через нее при разрядка конденсатора. Это напряжение по закону Кирхгофа равно напряжению q/С на конденсаторе, U_c=ε_S, поэтому:

или

или

(23.12)

где

(25.13)

Как видно, электрические колебания описываются таким же уравнением, что и механические, а потому подчиняются тем же закономерностям. Так, мгновенное значений заряда и напряжения на конденсаторе равны:

(25.14)

(25.15)

Ток в цепи меняется при этом по закону:

(25.16)

Как видно, изменение тока опережает изменение напряжения по фазе на π/2.

Период таких колебаний согласно (25.10) и (25.13) равен:

(25.17)

Найдем соотношение между амплитудами тока i₀ напряжения U₀:

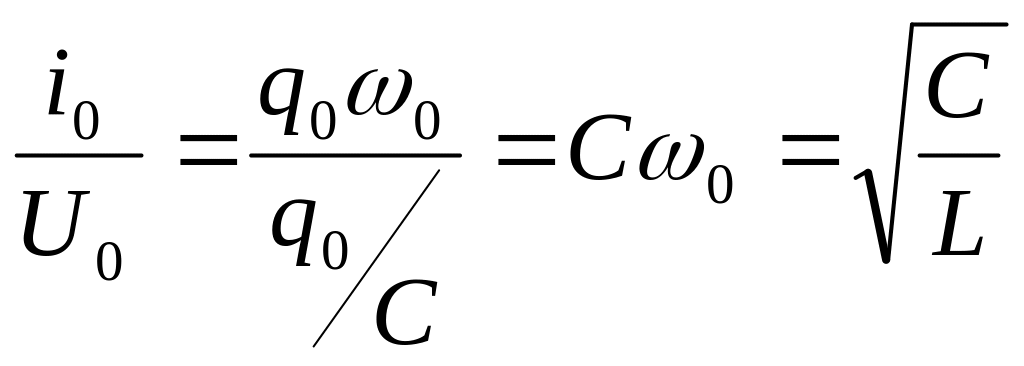или .

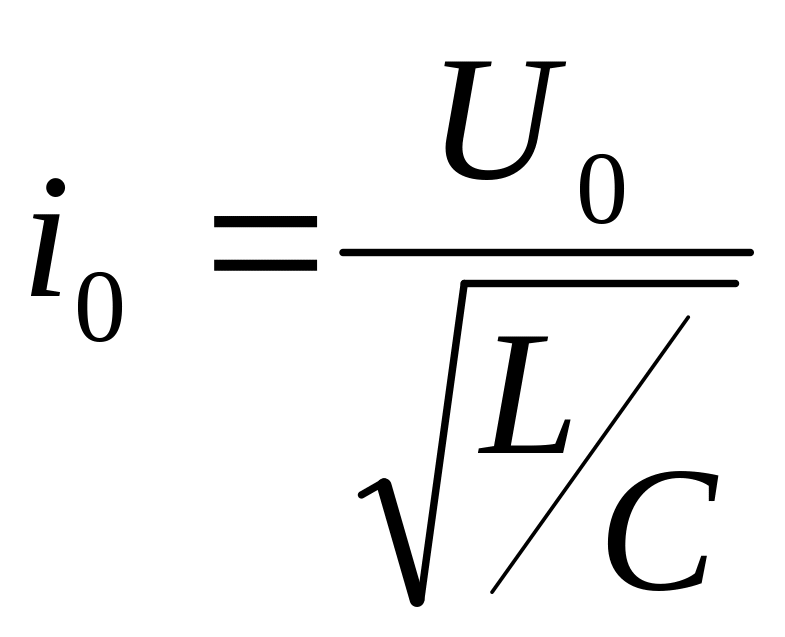Это соотношение аналогично закону Ома. Величина представляет особый вид сопротивления. Его называют волновым сопротивлением контура.

2. Сложение двух гармонических колебаний одного направления

Во многих физических явлениях наблюдаются не простые гармонические колебания, а более сложные, являющиеся суммой отдельных гармонических колебаний. Рассмотрим несколько случаев сложения колебании.

Колебания с одинаковыми частотами. Пусть первое движение описывается уравнением , а второе . Т.к. оба колебания имеют одинаковую частоту, то результирующее колебание будет иметь ту же частоту, но свою амплитуду A и начальную фазу θ:

X=Acos(ωt+θ) (25.18)

Для нахождения A и θ используют векторный способ представления колебаний (Рис.25.5): при вращении вектора с угловой скоростью ω его проекции на оси x и y совершают гармонические колебания относительно т.О. Т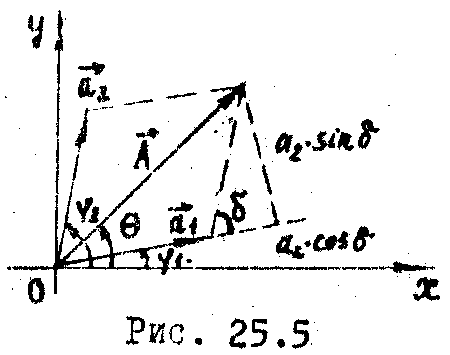 огда, как следует из чертежа:

(25.19)

где

Фаза θ для смещения определяется выражением"

(25.20)

Колебания с разными частотами. Если выражения для таких колебаний и , где ω₂>ω₁, то результирующее смещение будет:

(25.21)

Это выражение описывает косинусоидальные колебания со средней частото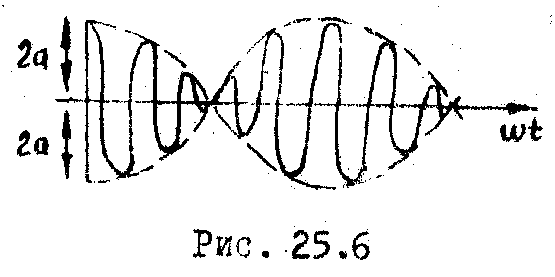й модулированной амплитудой A=2a,которая изменяется по закону косинуса с частотой (Рис. 25.6). Когда частоты ω₁ и ω₂ почти одинаковы, то частота косинусоидальной модуляции амплитуды очень мала. Такие колебания называют биениями.