2. Квантовомеханическое описание водородного атома

Результаты теории Бора для энергетических уровней электрона в атоме водорода получаются в квантовой механике без дополнительных постулатов, т.к. правило квантования, введен­ное Бором, искусственно является следствием волновых свойств электрона. Действительно, волна де Бройля, связанная с движе­нием электрона по орбите, должна укладываться на ней целое число раз (Рис. 35.1). Т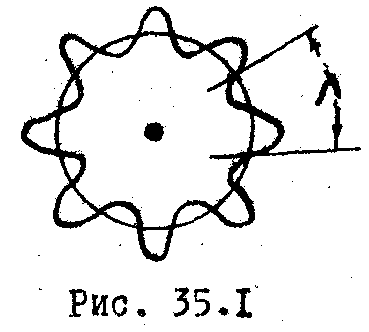 огда , т.к. , тo , откуда .

Т.о. получим уравнение первого постулата Бора. Состояние элек­трона в атоме водорода, соглас­но квантовой механике, описыва­ется стационарным уравнением Шредингера , где —

расстояние электрона до ядра.

Аналогично примеру, рассмотренному в лк. 34, состояние электрона будет описываться набором волновых функций, кото­рые в отличие от одномерной задачи теперь определяются не од­ним, а тремя квантовыми числами - n, l, m: . Эти чис­ла связаны с квантованием величин, характеризующих состояние электрона. Как и в примере для частицы в потенциальной яме, точное решение уравнения Шредингера для атома водорода приво­дит к появлению дискретных энергетических уровней. Каждому уровню соответствует целое главное квантовое число n =1,2,..., что совпадает о результатом теории Бора.

Состояние электронов в атоме может отличаться не только энергией, определяемой квантовым числом n, но величиной и направлением момента импульса. Момент импульса L сказывает­ся также квантованной величиной, и для каждого значения энер­гии Е_n принимает дискретный ряд значений:

(35.8)

где l - целые числа от 0 до (n-1): l=0,1,2,...,(n-1) -всего значений. Его называют орбитальным или побочным квантoвым числом.

Проекция момента импульса L_Z на любое направление также квантуется. Для каждого l момент импульса ориентируется так, чтобы

(35.9)

где m -целые числа от -l до +l, включая 0: m=0, ±1, ±2,..., ±l - всего (2l+1) значение. Его называют магнитным квантовым числом. Итак, уравнение Шредингера приводит к тому, что каждое квантовое состояние электрона в атоме водорода характери­зуется набором квантовых чисел n, l, m, который соответствует определенная энергия электрона, момент импульса и его проек­ция на выделенное направление. Подсчитаем число возможных сос­тояний электрона с данным квантовом числом n. Т.к. m при­нимает (2l +1) значение, а l может изменяться от 0 до n-1, то полное число состояний равно

(35.10)

Ниже приведены возможные состояния электронов в атоме. Если теория Б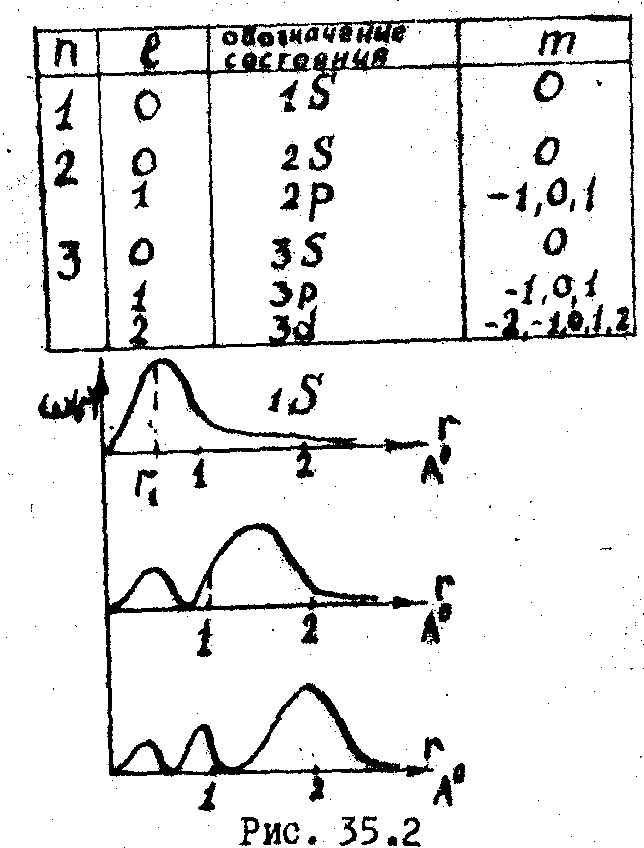 ора допускала наглядное представление состояния электрона в атоме с помощью орбит, то квантовая теория вообще не допускает существование орбит. Решение уравнения Шредингера позволяет находить -вероятность нахождения электро­на внутри заданного объема. На рис. 35.2. показаны распределе­ния вероятности для различных состояний электрона. Так, для основного состояния электрона 1S вероятность w(r) имеет мак­симум на расстоянии первой бо-ровской орбиты. Т.о.,боровские орбиты электрона в атоме предсдавляют собой геометрические места точек, в которых с наи­большей вероятностью может быть обнаружен электрон.