2. Физический смысл волн де Бройля.

Сравним результат дифракции световых волн и частиц. В результате наложения дифрагирующих волн происходит усиление или ослабление амплитуды колебаний. Степень почернения фото­пластинки (дифракционные максимумы) пропорциональна интенсив­ности волны, т.е. квадрату амплитуды световой волны.

Образование же дифракционной картины у частиц означает, что в равные точки экрана попадает различное число частиц. Так как попадание отдельных частиц в определенные места пластинки носит случайный характер, тo можно сказать, что частицы после прохождения фольги на одни участки фотопластинки попадают с большей вероятностью, а на другие - м меньшей. Мерой вероятности в данном случае является доля частиц, попадавших на данный участок.

Итак, в случае дифракции частиц степень почернения отдельных участков фотопластинки зависит от вероятности попада­ния частиц на эти участки, а в случае дифракции света степень почернения пропорциональна квадрату амплитуды волны. Отсюда можно заключить, что квадрат амплитуды волны де Бройля определяет вероятность нахождения частиц в данной области пространствa. В этом и заключается статистическое, вероятностное толкование волн, связанных с движущейся частицей.

3. Соотношение неопределенностей

Согласно физическому толкованию волн, связанных с движу­щимися частицами, нельзя утверждать, что при определенных ус­ловиях частица будет двигаться по строго определенной траек­тории. Можно лишь говорить о вероятности той или иной траек­тории. Т.е. наличие волновых свойств приводит к некоторой неопределенности (неточности) в описании движения частиц при помощи задания их координат и скоростей.

Однако в ряде случаев волновые свойства не сказываются на движении микрочастиц. Например, движение электронов в элек­тронно-лучевой трубке, з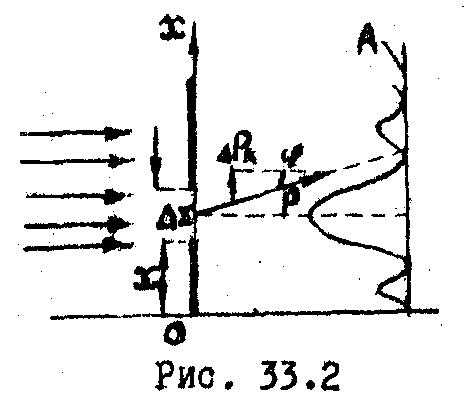 аряженных частиц в ускорителях. Т.о., необходим критерий , чтобы судить в каких случаях надо учиты­вать волновые свойства частиц, а когда ими можно пренебречь. Таким критерием и служит соотношение неопределенностей, полу­ченное в 1925 г. В.Гейзенбергом.

Получим его, рассмотрев прохождение электронного пучка сквозь щель ширины Δх (рис. 33.2). Т.к. электроны обладают волновыми свойствами, то после прохождения щели произойдет диф­ракция, и на фотопластинке А об­разуется дифракционная картина. Из формулы дифракционной решетки (лк.30) для первого максимума имеем

(33.5)

Используя формулу (33.1), получим и

(33.6)

Т.о., после прохождения щели стали известны с точностью до Δх координаты электрона, но зато появилась неопределен­ность в составляющей импульса . Из (33.6) можно записать соотношение между Δх и Δр_х:

Т.к. для некоторой части электронов, попадающих за преде­лы главного максимума, , то

(33.7)

Это и есть соотношение неопределенностей.

Для расчетов удобно пользоваться соотношением

(33.8)

Из этой формулы видно, что из-за малости h значительная неопределенность в скорости может быть лишь для микроскопических частиц. Для макроскопическик частиц ΔV пренеб­режимо мала, и их волновые свойства не играют роли. Для примера рассмотрим два случая:

1) движение электронов в электронно-лучевой трубке. След элек­тронного луча можно определить в пределах . Тогда из (33.8) находим :

Учитывая, что , видно, что и для описания движения электронов в этом случае можно пользоваться законами Ньютона, не учитывая волновых свойств;

2) движение электронов в атоме водорода. Если электрон принадлежит атому, то, его координаты должны лежать в пределах атома, т.е. . Тогда . Скорость же движения электрона в атоме V~10⁶м/с. Т.е. неопределенность в скорости соизмерима со скоростью. Поэтому для описания движения электрона в этом случае нельзя ис­пользовать законы Ньютона, а надо учитывать его волновые свойства.

Лекция 44	Волновая функция и её статический смысл. Уравнение Шредингера. Стационарные состояния.
	Свободная частица. Частица в одномерной прямоугольной потенциальной яме.