2. Фотон и его свойства

Итак, наряду с волновыми свойствами как интерференция и дифракция, свет обладает и такими, для объяснения которых пришлось предположить, что колеблющиеся заряды в атомах могут излучать и поглощать свет только определенными порциями энергии - квантами. Величина энергии кванта равна

(32.10)

В тех случаях, когда необходимо подчеркнуть корпускуляр­ные свойства света, говорят о световых частицах - фотонах, квантами же называют порцию энергии.

Если предположить, что свет распространяется в пространстве как поток особых частиц, то следует считать, что они об­ладают массой и импульсом. Согласно взаимосвязи массы и энер­гии в теории относительности (лк. 6) E=mc², поэтому каж­дому фотону можно приписать массу

(32.11)

Отличие этой массы от массы макрочастиц в том, что фотон не имеет массы покоя m₀. Это следует из формулы (лк. 6) . Для фотона V=С и β=1, так что . Для получения конечного значения m необходимо условие: m₀=0. Это и понятно, т.к. фотон - частица движения. Импульс фотона можно найти из соотношения (лк. 6) Т.к. m₀=0, то

(32.12)

Это выражение можно переписать:

(32.13)

где

Если ввести в рассмотрении волновой вектор к, совпада­ющий по направлению с распространением света, то

(32.14)

Между .длиной волны света λ и импульсом фотона суще­ствует связь, которая устанавливается из соотношения . Подставив это в (32.12), находим

(32.15)

Итак, фотон обладает энергией, массой и импульсом. Откры­тие у света корпускулярных свойств но отрицает наличие у него волновых. Корпускулярные свойства проявляются, главным образом, при излучении и поглощении света особенно большой частоты.

Элементы атомной физики и квантовой механики

Лекция 43	Опытное обоснование корпускулярно-волнового дуализма вещества. Формула Луи де Бройля.
	Соотношение неопределённостей Гейзенберга.

1. Волновые свойства частиц

Как видно из предыдущей лекции, между светом и частицами существует много общего: свет обладает рядом корпускулярных свойств, которые характеризуются теми же величинами, что и свойства частиц. В 1924 г. де Бройль высказал предположение, что если свет обладает корпускулярными свойствами, то и части­цы в свою очередь должны обладать волновыми свойствами. При этом формулы, описывавшие свойства света и частиц, должны сов­падать. Так, длина волны частицы о массой т, движущейся со скоростью v, должна определяться формулой (32.15), т.е.

(33.1)

Эту волну, связанную с движущейся частицей, принято назы­вать волной де Бройля. Существование этих волн может быть установлено лишь на опыте, где проявляется волновая природа частиц. Т.к. волновые свойства света проявляются в явлениях интерференции и дифракции, то для частиц, если гипотеза де Бройля верна, также должны обнаруживаться эти явления. Одна­ко вследствие очень малых длин волн де Бройля обнаружить вол­новые свойства частиц значительно трудней, чем у света. Прос­тые вычисления по формуле (33.1) дают, например, для электро­нов в электронно-лучевой трубке значения λ: скорость элек­трона определяется соотношением , где U - ускоряющее напряжение (~ 2 кВ), откуда и , в то время как длина волны видимого света ~ 5500А.

Как известно, дифракция обнаруживается, когда размеры препятствий соизмеримы с длиной волны (лк.30 п.2). Поэтому дифракцию частиц можно обнаружить не на оптической дифракцион­ной решетке, а на кристалле, расстояние между атомами в ко­тором составляет, ~10^-10м. Такие опыты были проделаны и под­твердили наличие у частиц волновых свойств. Это опыты К.Д.Дэвисона и Л.X. Джермера по дифракции электронов на кристалле Li, Дж.П.Томпсона и П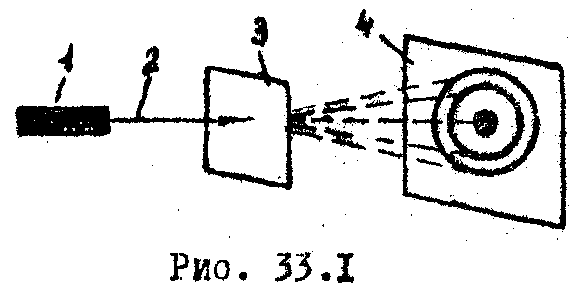 .С.Тартаковского по дифрак­ции электронов с помощью фольги. Впоследствии такие опыты были проделаны с пучками нейтронов и протонов, а О.Штерн провел опыты с атомами гелия и натрия. Схема одного из таких опытов приведена на рис. 33.1. Здесь 1 - электронная пушка, 2 - электронный пучок, 3 - фольга (толщина 10^-5+10^-6см), 4 - фотопластинка. После проявления на фотопластинке был виден ряд светлых и темных концентрических колец, т.е. типичная дифракционная картина, по кото­рой можно было рассчитать длину волны и сравнить с (33.1). Оказалось, что результаты таких расчетов хорошо совпадают, и, следовательно, гипотеза де Бройля подтверждается экспериментально.