3. Дифракция на щелях

При прохождении света через узкую щель также наблюдается дифракция. Пусть цель шириной а освещается пучком параллель­ных лучей, которые, проходя ее, дифрагируют на различные углы φ (Рис.30.3). В соответствии с принципом Гюйгенса-Френеля плоский фронт АВ разобьем на зо­ны, в качестве которых в данном случае выберем узкие полоски ши­риной х. Т.к. разность хода между л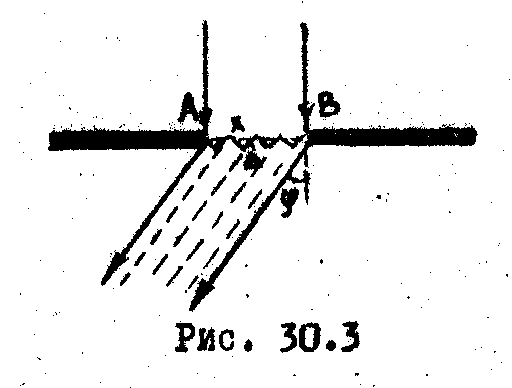 учами соседних зон то ширина зоны равна , а число зон, уложившихся на ширине АВ=а, равно

(30.6)

В соответствии с (30.3), если m=2n (четное), то в со­ответствующем направлении дифракции будет ослабление осве­щенности, если m=2n+1 (нечетное), то усиление освещен­ности. Итак, условие максимумов будет

или (30.7)

Условие минимумов будет

или (30.8)

Зависимость освещенности от угла дифракции изображена на риc.30.4. Если взять две щели, то распределение освещен­ности изменится. Пусть непрозрач­ный экран с двумя щелями шириной a, отстоящих друг от друга на расстоянии b, освещается параллельным пучком света (Рис. 30.5).

В тех направлениях, в которых ни одна из щелей свет не распространяет, будут наблюдаться прежние минимумы. Что касается максимумов, то они будут наблюдаться не во всех направлениях, как для одной щели. Вследствие интерференции соответствующих лучей соседних щелей (1,3; 2,4 ) в некото­рых н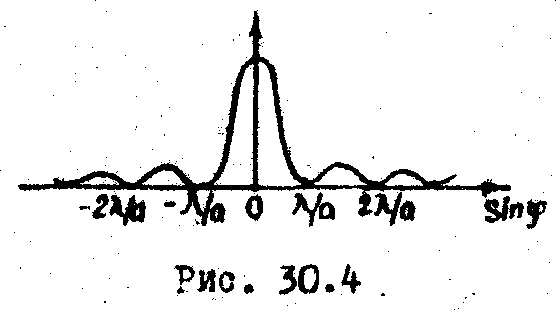 аправлениях они будут взаимно уничтожаться. Следователь­но, в отличие от дифракции на одной щели возникнут добавочные минимумы. Они возникнут в тех направлениях, которым соответ­ствует разность хода (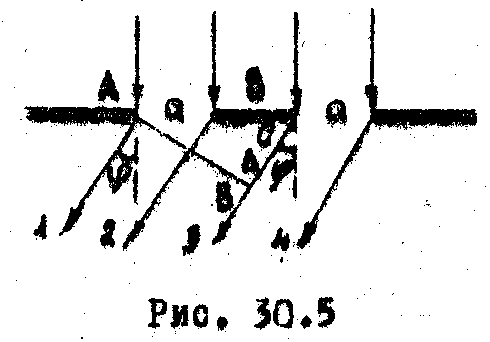условие минимумов при интер­ференции), т.е., если а+в=1 , то

(30.9)

Действие одной щели будет усиливать­ся другой в тех направлениях, которым, соответствует разность хода λ, 2λ,… (условие интерференционного макси­мума), т.е.

(30.10)

Т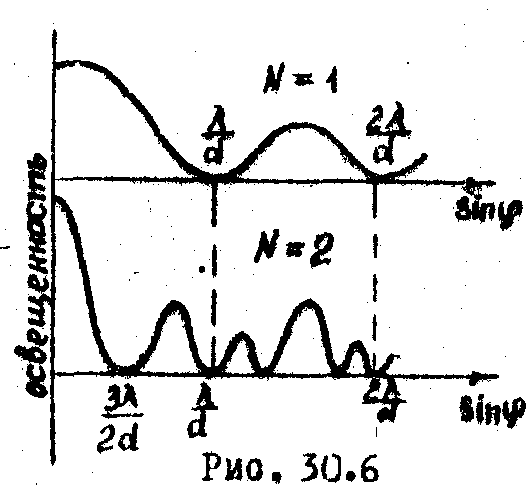 акие максимумы называется плавными. Т.о., в случае двух щелей наряду с прежними минимумами - главными мини­мумами, определяемыми (30.8), возникают добавочные минимумы, определяемые (30.9), и главные максимумы - (30.10). Сравнительное распределение освещенностей для 1-й и 2-й щелей показано на рис.30.6. Как видно, появление добавочных минимумов приводит к перераспределение интенсивности.

4. Дифракция света от многих щелей. Дифракционная решетка

Как видно, в случае двух щелей между соседними главными максимумами появляется один добавочный минимум. Аналогично для N=3 между соседними максимумами появится два добавочных минимума и т.д. Для N щелей число добавочных минимумов равно N-1. Т.о., дальнейшее увеличение числа щелей приводит к дальнейшему перераспределению освещенности, и дифракционная картина - дифракционный спектр при большом числе щелей будет состоять из отдельных узких светлых линий, разде­ленных темным промежутком.

Система параллельных целей, разделенных непрозрачными промежутками, называется дифракционной решеткой. Расстояние между щелями d=a+b называют периодом решетки.

Основными характеристиками решетки являются: общее число штрихов N , число штрихов на единицу длины .

Главные максимумы возникают при условии (30.10), которое называют формулой дифракционной решетки:

(30.11)

Из этой формулы следует, что дифракционная решетка осу­ществляет спектральное разложение, т.к. свет с разной длиной волны отклоняется на разные углы. Если решетку освещать белым светом, то все максимумы кроме нулевого становятся окрашенны­ми. Число m называют порядком дифракционного спектра, оно определяет число главных максимумов, которое равно , т.к. . Как видно, с помощью дифракционной решетки можно измерить длину волны света, для чего надо по заданному d измерить φ. Важнейшей характеристикой решетки является ее разрешающая способность, характеризующая свойство решетки раз­делить (наблюдать раздольно) две близкие длины волны. Эта ве­личина определяется формулой

A=mN, (30.I2)

где m - порядок спектра, N - общее число щелей, - длина волны, вблизи которой ведется измерение, . Здесь λ₁ и λ₂ - длины волн, которые надо разрешить.

Лекция 39	Естественный и поляризованный свет. Закон Брюстера.
	Двойное лучепреломление. Закон Малюса. Поляроиды и поляризационные призмы.