1. Принцип Гюйгенса-Френеля

Наряду с интерференцией подтверждением волновой природы света является дифракция света. Под дифракцией света пони­мают всякое отклонение распространения света от прямолинейного, загибание света в область геометрической тени. Если диф­ракция звуковых волн наблюдается повседневно, тo для наблю­дения дифракции света необходимы специальные условия, что объясняется малой длиной волны. Так, например, проходя сквозь малое отверстие н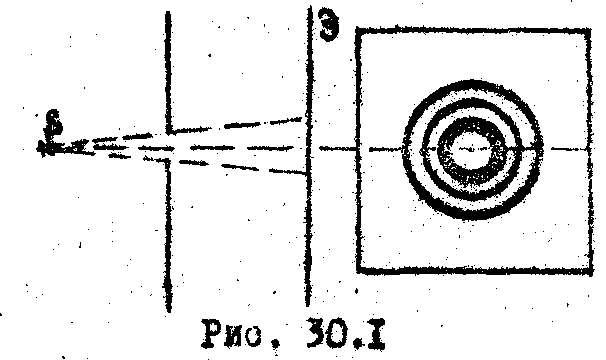 а экране, обнаруживается не четкая граница между светом и тенью, а чередую­щиеся светлые и веяные кольца, подобно интерференции (Рис.30.1). Огибание волнами препятствий можно объяснить с помощью принци­па Гюйгенса (см.лк.27). Для объяснения чередующихся максимумов и минимумов освещенности Фре­нель дополнил этот принцип идей об интерференции вторичных волн. В таком объединенном виде объяснение дифракции света называют принципом Гюйгенса-Френеля. Т.о., задача дифракции сводится к довольно сложной математической задаче об интер­ференции от многих источников.

Как показал Френель, в случаях, отличающихся симметрией, амплитуду результирующего колебания можно найти простым ал­гебраическим сложением амплитуд от вторичных волн. Этот метод называют методом зон Френеля.

2. Метод зон Френеля. Прямолинейное распространение света

В качестве примера рассмотрим распространение сферичес­кой световой волны от точечного источника S и найдем ампли­туду светового колебания А в некоторой точке наблюдения Р (Рис. 30.2). Согласно Френелю волновой фронт разбивают на от­дельные участки - зоны так, чтобы расстояние от каждой до точки Р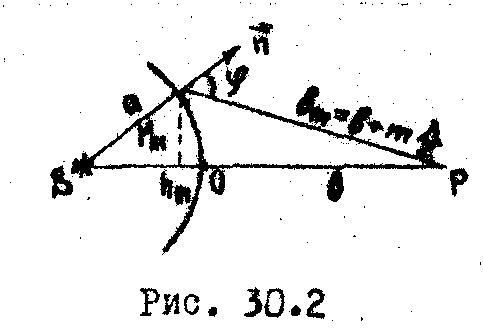 отличались на :

(30.1)

При таком разбиении зоны Френе­ля - шаровые пояса, а первая -шаровой сегмент. Т.к. ревность хода соседних волн , то коле­бания в т.Р приходят в противо­фазе и взаимно гасят друг друга, так что в т.Р дойдет ко­лебание лишь от первой зоны:

(30.2)

С ростом номера зоны растет b_m и угол между норма­лью к поверхности зоны и направлением на т.Р (угол φ), поэ­тому амплитуда колебания A_m, возбуждаемого m-й зоной в т.Р, монотонно убывает с ростом m. Поэтому и все выражения в скобках в (30.2) равны нулю. Тогда вместо (30.2) получим

(30.3)

где "+" для m - нечетного, "-" для m - четного.

Итак, для большого числа зон Френеля амплитуда результирующего колебания будет равна , т.е. определяться половиной амплитуды первой зоны. Вычислим площадь зоны. Для 1-й зоны . Из рис. 30.2 находим:

и

Для площади сегмента, представляющего две первые зоны аналогично, найдем , а . Т.е. площади всех зон одинаковы и для данного случая равны:

(30.4)

Так λ~5∙10^-6м, а~b~1м и S~1мм². Следовательно, распространение света от S к P происходит так, как если бы свет распространялся внутри - прямолинейное распространение света.

Найдем соотношение между волновой и геометрической опти­кой. Для этого подсчитаем число зон Френеля, уложившихся на круглом отверстии радиуса R: . Принимая а~b, получим . Если отверстие большое, т.е. число зон велико (m>>1), наблюдаем прямолинейное распрос­транение света. Если отверстие мало, т.е. число зон ограничено (m~I), проявляется дифракция, результат которой определитcя (30.3). Итак:

(30.5)

В качестве R можно рассматривать линейный размер препятствия, в качестве b - расстояние либо от препятствия до точки наблюдения, либо от источника света до препятствия.