2.3. Граничные условия

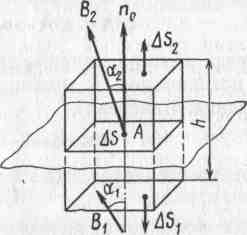
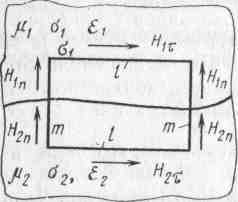
При анализе электромагнитного поля важно учесть граничные условия на поверхности раздела двух сред, где параметры ε_r, μ_r и σ могут изменяться скачком, что, в свою очередь, приводит к скачкообразному изменению векторов поля. Эти векторы как функции координат перестают быть непрерывными, в результате oпepaции rot и div на границах раздела теряют смысл, т. е. уравнения Максвелла здесь не могут быть записаны. На рис. 2.5 показан участок границы, разделяющий две среды. Условно выделен прямоугольный контур, две стороны которого длиной l параллельны

Рис. 2.5. Условия на границе Рис. 2.6. Условия на границе раздела

раздела двух сред для танген - двух сред для нормальных

циальных составляющих составляющих векторов

векторов

участку границы, а две другие длиной т ортогональны ему. Тогда, устремляя к нулю размер стороны т контура, ортогональной границе, получим, что слагаемые для циркуляции вектора Н вдоль этих сторон в выражении для закона полного тока также стремятся к нулю. В результате выражение закона полного тока принимает вид

. (2.36)

Но так как dS = ml стремится к нулю при m→0, то граничное условие для тангенциальных составляющих вектора напряженности магнитного поля имеет вид

. (2.37)

Аналогично получаются граничные условия для нормальной составляющей магнитной индукции. В этом случае рассматривается поток вектора В через поверхность призмы, внутри которой проходит граница раздела двух сред (рис. 2.6). Если высота призмы h стремится к нулю, верхнее и нижнее основания приближаются к границе и уравнение (2.7) записывается в виде разности скалярных произведений:

. (2.38)

Отсюда с учетом равенства ΔS₁ = ΔS₂ получаем граничное условие для нормальных составляющих вектора магнитной индукции:

В_1п = В_2п. (2.39)

Аналогично получаются граничные условия для составляющих векторов электрического поля на границе раздела двух сред:

, , , (2.40)

где σ_пов — плотность поверхностного заряда.

Кроме граничных должны быть также заданы начальные условия, определяющие магнитное и электрическое состояния среды, соответствующие моменту времени, принятому за начало отсчета. Начальные условия специфичны для каждого конкретного случая неразрушающего контроля и в необходимых случаях будут специально рассматриваться.

Теперь рассмотрим частные случаи электростатического и маг-нитостатического полей.

Электростатическое поле — это такой частный случай электромагнитного поля, когда магнитное поле отсутствует, заряженные тела неподвижны и

Система уравнений Максвелла для электростатического поля имеет вид

. (2.41)

Из условия rot E = 0 в соответствии с формулой Стокса следует, что не зависит от пути интегрирования. Поэтому можно ввести понятие потенциала φ электростатического поля:

. (2.42)

Теперь, исключив вектор D из системы (2.41):

, (2.43)

получим уравнение

(2.44)

или для областей, где отсутствуют свободные заряды,

. (2.45)

Практический интерес представляет случай расчета электрического поля в кусочно-однородной среде, где для каждого участка среды величина ε_а постоянна и ее можно вынести за знак дивергенции. Тогда уравнения примут вид

,

. (2.46)

Первое выражение называют уравнением Пуассона, второе — уравнением Лапласа. В символической форме соответственно их записывают в виде

или ,

или .

В электростатике уравнение Лапласа имеет исключительно большое значение. Для отыскания решения этого уравнения его чаще всего записывают в координатной форме, подставляя в выражение для divE значения составляющих вектора Е:

, , . (2.47)

Тогда получаем

. (2.48)

Формально уравнения Лапласа и Пуассона можно записать используя символические операторы и производя с ними те же действия, что и с обычными векторами:

. (2.49)

Умножив далее на величину φ, приходим к уравнениям Лапласа и Пуассона.

Рассмотрим граничные условия для двух практически важных случаев электростатического поля. В одном случае это граничные условия на поверхности проводников, когда в электростатическом поле отсутствуют электрические токи: J = 0. Отсюда с учетом того, что J = σE, следует, что внутри проводников, т. е. там, где σ ≠ 0, выполняется соотношение

Е = 0. (2.50)

Но из уравнения Е= - gradφ следует, что потенциал всех точек проводника, в том числе и точек поверхности, имеет одно и то же значение, т. е. поверхности проводников эквипотенциальны. Следовательно, на поверхности проводника в электростатическом поле

Е_τ = 0. (2.51)

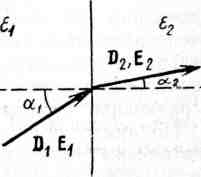
Рис. 2.7. Изменение направления векторов при переходе через границу раздела двух сред.

Отсюда получаем граничные условия для напряженности электрического поля в диэлектрике на поверхности раздела проводника и диэлектрика:

Е_х=0, Е_п = Е =- дφ/дп. (2.52)

При этом .

В другом случае это граничные условия на поверхности раздела двух диэлектриков. При отсутствии свободного поверхностного заряда (σ_пов = 0)

D_ln=D_2n. (2.53)

Кроме того, всегда выполняется соотношение (2.40). Отсюда можно получить зависимость между векторами D и E при переходе из одной среды в другую. Согласно обозначениям (рис.2.7)

. (2.54)

Учитывая соотношения

, , (2.55)

получаем . (2.56)

Если линии напряженности электрического поля ортогональны поверхности раздела, то D₁ = D₂, а напряженность электрического поля изменяется скачком:

. (2.57)

Общей задачей расчета электрического поля является определение напряженности электрического поля Е во всех его точках по заданному распределению зарядов. При этом достаточно определить распределение потенциала. Если задано распределение электрических зарядов в однородной среде, то решение отыскивается методом суперпозиции. Это так называемая прямая задача, решаемая следующим образом. Для каждого заряда q_i определяется создаваемая им составляющая напряженности электрического поля:

, (2.58)

а затем составляющая потенциала φ, соответствующая этому заряду:

. (2.59)

Далее суммированием (или интегрированием) по всем зарядам определяются напряженность электрического поля Е и потенциал φ в каждой точке пространства.

Обратная задача значительно сложнее и решается с помощью уравнений Лапласа и рассмотренных граничных условий. Так как распределение зарядов по поверхности тел неизвестно, то решение сильно затрудняется. Особенно сложной является задача в случае неоднородных сред. Решить ее аналитическим путем удается для ограниченного числа частных случаев.

По аналогии с электрическим полем определяется и магнито-статическое поле, именно как частный случай электромагнитного поля, когда отсутствует электрическое поле, нет электрических зарядов и тока. Система уравнений Максвелла для магнитостатического поля имеет вид

rot Н=0, div В=0. (2.60)

Из первого условия формально можно ввести понятие скалярного магнитного потенциала

H=-gradφ_м, (2.61)

который часто используется при решении магнитостатических задач.

Главной особенностью и сложностью многих магнитостатических задач является то, что их очень часто приходится решать для анизотропных сред с неоднозначной зависимостью В(Н) в виде семейства петель гистерезиса.