Задание №6

Привести по своему выбору 3 разных примера графиков функций, которые имеют 4 точки разрыва 2 – первого рода и 2 второго рода.

1. f(x)=

Разрыв II рода в точках 1 и -1. Разрыв I рода в точке 2 и 3. (рис. 1)

2. f(x)=

Разрывы II рода в точках -2 и 0. Разрыв I рода в 2 и 4. (рис. 2)

3. f(x)=

Разрывы II рода в точках-1,5 и 0,5 . И I рода в точках 1 и 3. (рис. 3)

рис. 1 рис. 2

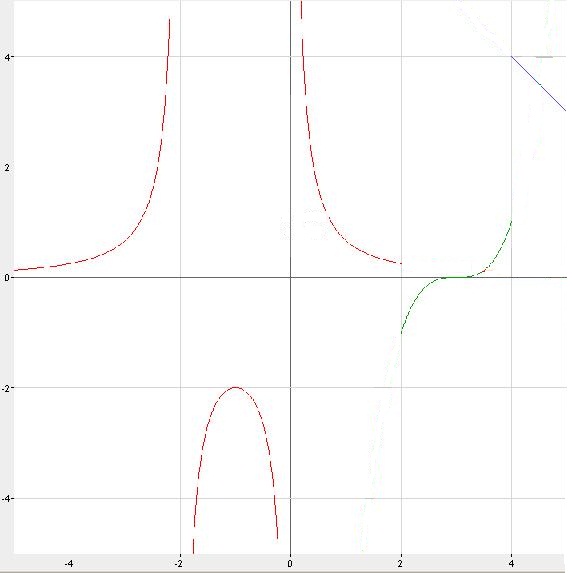Рис. 3

Задание №7

Привести по своему выбору 3 разных примера графиков функций, которые являются непрерывными, но не гладкими в 5 точках их области определения, так что в этих точках левые производные - отрицательные, а правые производные – положительные.

Рис. 4. Пример графика функций №1

Рис. 5. Пример графика функций №2

Рис. 6. Пример графика функций №3

Задание № 8

Привести по своему выбору 3 разных примера двух множеств на числовой прямой или плоскости, которые:

• являются ограниченными, открытыми и эквивалентными по мощности (конечной, счетной, несчетной),

• являются неограниченными, счетными, не совпадающими, но имеющими бесконечное число точек в их пересечении.

Множество R (действительных чисел) [0;1] не является счетным;

1. A = { x : и B = { x : ;

и ;

и .

2. и

и

Задание №9

Изложить свои соображения по вопросу:

• почему операция умножения матриц не является коммутативной,

• привести пример, по своему выбору, конкретных матриц 3x3, когда при их умножении коммутативность все же будет иметь место.

Произведением матрицы A=(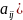 размерности m*n на матрицу B=( размерности n*k называется матрица С=( ) размерности m*k, где

т.е элемент матрицы матрицы С равен сумме произведений элементов p-й строки матрицы А на соответствующие элементы t-го столбца B.

Свойство коммутативности

A*B=B*A

Данное свойство может выполняться, а может и нет.

Докажем исходя из определения: размерность матрицы m*n умноженной на матрицу размерности n*k будет матрица m*k матрица 3*2 умноженная на 2*5 будет матрица 3*5. А умножить матрицу 2*5 на матрицу 3*2 нельзя.

Значит для коммутативности нужно использовать только квадратные матрицы.

Из опыта можно найти 4 разных случая, когда при умножении матриц будет иметь свойство коммутативности.

1. Одна из матриц является единичной.

2. Одна из матриц является нулевой.

3. Обе матрицы имеют одинаковые элементы т.е они равны.

4. Вспомним правило треугольника для нахождения определителя. Чтобы найти определить нужно взять с плюсом и вычислить элементы .

Так вот если элементы на плюсе равны и матрица B является транспонированной матрицей А. То коммутативность имеет смысл.

, .

5. Умножение двух диагональных матриц коммутативно.

Задание №10

Как восстановить элементы матрицы в заданном базисе, если известны её собственные числа и собственные вектора, всегда ли решение будет единственным? Привести, по своему выбору, соответствующие примеры.

Пусть

A* =λ* ,

λ-некоторое число.

Ненулевой вектор , удовлетворяющий этому условию, называется собственным вектором линейного преобразования А, а соответствующее число λ называется собственным числом. Исходя из этого можно по собственным числам и векторам восстанавливать матрицы.

где координаты первого собственного вектора, а первое собственное число.

Для вторых собственных векторов и чисел составляем такие же уравнения. Если будет больше векторов, то больше уравнений делаем, затем объединяем уравнения с одинаковыми коэффициентами.

На данном примере мы получаем две системы уравнений.

и

Выражая один неизвестный коэффициент через другой. Находим a,b,c,d. Т.е элементы нашей матрицы.

Пример с матрицей 2 x 2.

Собственные числа 1 и . Собственные вектора и

и

a=b+1 => b+1+b=3=>b=1; c=d-1=>d-1+d=3=>2d=2=>d=1;

a-1=1 => a=2; c-1=-1=>c=2;

Наша матрица A=

Пример с матрицей 3 x 3.

Собственные числа 6 , . Собственные вектора , и

Решая эти уравнения, находим что наша матрица A=

Решения не всегда будут единственными, т.к иногда появляются независимые переменные в векторе.