Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт Космических и информационных технологий

Кафедра Вычислительной техники

Отчет по практике

Вариант 5

Студент КИ11-08Б 04.10.12 Яровая Д. С.

номер группы подпись, дата инициалы, фамилия

Преподаватель Кошур В.Д.

подпись, дата инициалы, фамилия

Красноярск 2012

Содержание

Y

Задание №1 3

Задание №2 4

Задание №4 9

Задание №5 11

Задание №6 13

Задание №7 14

15

Задание №9 17

Задание №10 18

Задание №1

Подготовить реферат на тему: Тема варианта N, объемом 7-15 страниц и быть готовым к собеседованию по этой теме.

Вариант 5. Тема: Введение в методы оптимизации.

См. приложение 1.

Задание №2

Научиться строить графики функций Y=f(X) и поверхностей функций Z=F(X,Y). Для визуализации использовать графические средства MATHCAD и MATLAB. В отчете кратко описать порядок построения и привести по своему выбору 4 рисунка для разных функций одной и двух переменных (по 2 примера – график и поверхность в MATHCAD и MATLAB).

Построение графиков в MATHCAD.

Построим функцию:

1. Напишем эту функцию в главном окне.

2. Перейдём в меню графиков.

3. Создадим линейный график, в нём укажем промежутки и аргументы функции f(x) и x.

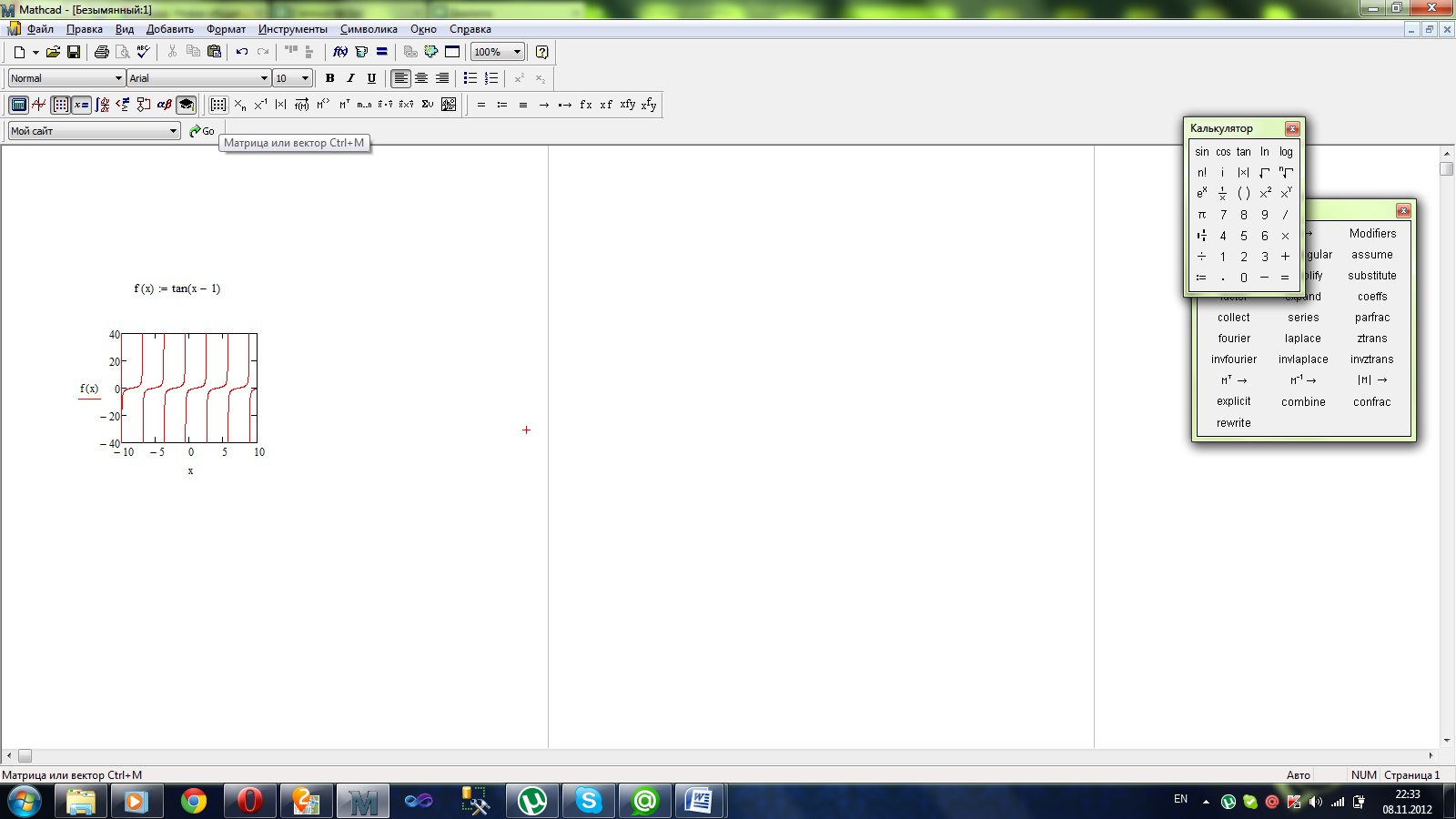
Рисунок 1. Линейный график в MATHCAD.

Построим функцию:

1. Напишем эту функцию в главном окне.

2. Перейдём в меню графиков.

3. Создадим поверхностный график, в левом нижнем углу укажем имя функции, f.

Рисунок 2. Объёмный график в MATHCAD.

Построение графиков MATLAB.

Построим функцию: tg(x)

1. Зададим вектор абсцисс узловых точек функций. X=0:0.5:10

2. Используем команды для построения графиков функции: plot(x,tg(x))

Рисунок 3. Линейный график в MATLAB.

Построим функцию

1. Определим матрицы с X и Y координатами точек сетки: [X,Y]=meshgrid(0:.1:5,0:.1:5); или [X,Y]=meshgrid(0:.1:5,0:.1:5)

2. Зададим функцию: Z=

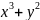
3. Создадим объёмный график с помощью команды: mesh(X,Y,Z)

Рисунок 4. Объёмный график в MATLAB.

Задание №3

Привести, по своему выбору, по 2 примера теорем из математических курсов, в которых используются:

• необходимые условия.

• достаточные условия.

• условия эквивалентности.

Необходимые условия:

1. Необходимое условие экстремума

Если функция нескольких переменных u = f(x1, x2, … , xn) имеет экстремум в некоторой точке, то в этой точке каждая ее частная производная равна нулю или не существует.

2. Необходимое условие интегрируемости по Риману.

Если функция интегрируема на отрезке, то она ограниченна на нём.

Достаточные условия:

1. Первый достаточный признак экстремума

Если производная f '(x) функции f(x) обращается в нуль в точке x₀ или не существует и при переходе через x₀ меняет свой знак, то функция f(x) имеет в этой точке экстремум (максимум, если знак меняется с "+" на "-", и минимум, если знак меняется с "-" на "+").

2. Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x ( a, b ), то функция  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x ( a, b ), то функция  f ( x ) является выпуклой на интервале ( a, b ) .

Условия эквивалентности:

Если из предложения А следует предложение В, то говорят, что В – необходимое условие для А, а А – достаточное условие для В.

Другими словами, предикат В(х) логически следует из предиката А(х), т.е. А(х) В(х), то А(х) называют достаточным условием для В(х), а В(х) – необходимым условием для А(х).

Если же предложения А и В равносильны, то говорят, что А – необходимое условие для В, и наоборот. Другими словами, если из предиката А(х) логически следует предикат В(х), а из предиката В(х) логически следует предикат А(х),т.е. А(х) В(х), то А(х) – необходимое и достаточное условие для В(х), а В(х) – необходимое и достаточное условие для А(х).

Теорема Кронекера – Капелли

Для совместности системы необходимо и достаточно, чтобы ранг матрицы коэффициентов А этой системы был равен рангу ее расширенной матрицы.