
- •Тема III – основы математического анализа
- •§8. Множества и операции над ними
- •8.1. Основные понятия
- •8.2. Числовые множества
- •9. Функция
- •9.1. Понятия функции и ее графика
- •9.2. Способы задания функций
- •9.3. Некоторые свойства функций
- •9.4. Обратная функция
- •9.5. Основные элементарные функции
- •9.5. Сложная функция и элементарные функции
- •§10. Предел функции
- •10.1. Предел функции в точке
- •10.2. Односторонние пределы
- •10.3. Предел функции на бесконечности
- •10.4. Бесконечно большие функции
- •§11. Бесконечно малые функции
- •11.1. Определение и основные теоремы
- •11.2. Основные теоремы о пределах
- •11.3. Техника вычисления пределов. Примеры
- •11.4. Первый замечательный предел
- •11.5. Эквивалентные функции
- •11.6. Второй замечательный предел
- •11.7. Техника вычисления пределов вида .
- •§12. Непрерывность функции
- •12.1. Непрерывность функции в точке и в области
- •12.2. Основные теоремы о непрерывных функциях
- •12.3. Классификация точек разрыва
- •§13. Производная функции
- •13.1. Приращение аргумента и приращение функции
- •13.2. Определение производной функции в точке
- •13.3. Геометрический смысл производной
- •13.4. Физический смысл производной
- •13.5. Дифференцируемость функций
- •13.6. Производная постоянной, суммы, произведения и частного двух функций
- •13.7. Производная сложной и обратной функции
- •13.8. Производные основных элементарных функций
- •13.9. Производная функции, заданной неявно
- •13.10. Логарифмическая производная
- •13.11. Производная функции, заданной параметрически
- •13.13. Примеры вычисления производных
- •13.14. Производные высших порядков
- •§14. Дифференциал функции
- •14.1. Понятие дифференциала функции
- •14.2. Основные теоремы о дифференциалах
- •14.3. Применение дифференциала к приближенным вычислениям
- •§15. Исследование функций при помощи производных
- •15.1. Правило Лопиталя
- •15.2. Некоторые теоремы о дифференцируемых функциях
- •15.3. Исследование поведения функций и построение графиков
- •Общее исследование функции и построение ее графика рекомендуется выполнять по следующей схеме:
Тема III – основы математического анализа
Под математическим анализом понимают систему дисциплин, предметом изучения которых являются количественные соотношения действительного мира, которые выражаются при помощи числовых величин (постоянных и переменных) и характеризуют некоторые процессы. Известно, что уже древнегреческие математики пользовались некоторыми методами математического анализа, а систематическое развитие эти методы получили в XVII веке.
§8. Множества и операции над ними
8.1. Основные понятия
В
основах математического анализа лежит
понятие множества.
Данное
понятие в математике не определено. Под
множеством
понимают совокупность некоторых
объектов, объединенных по какому либо
признаку. Объекты, из которых состоит
множество, называются его элементами.
Множество принято обозначать заглавными
буквами латинского алфавита: А, В, Х…,
а их элементы – малыми буквами a,
b,
x.
Если элемент принадлежит множеству Х,
то пишут
![]() и
и
![]() в случае, если элемент не принадлежит
множеству X.
Множество, не содержащее ни одного
элемента, называется пустым,
его обозначают .
Множество можно задать либо перечислением
его элементов, либо указанием правила
по которому элементы объединены в данное
множество. Например, множество X={дедка,
бабка, внучка, жучка, кошка, мышка} или
X={x:
x
– участник
сбора урожая репы}.
в случае, если элемент не принадлежит
множеству X.
Множество, не содержащее ни одного
элемента, называется пустым,
его обозначают .
Множество можно задать либо перечислением
его элементов, либо указанием правила
по которому элементы объединены в данное
множество. Например, множество X={дедка,
бабка, внучка, жучка, кошка, мышка} или
X={x:
x
– участник
сбора урожая репы}.
Множество A называется подмножеством множества В, если каждый элемент множества А является элементом множества В (обозначается
 ).
).Множества, состоящие из одних и тех же элементов, называются равными (обозначается
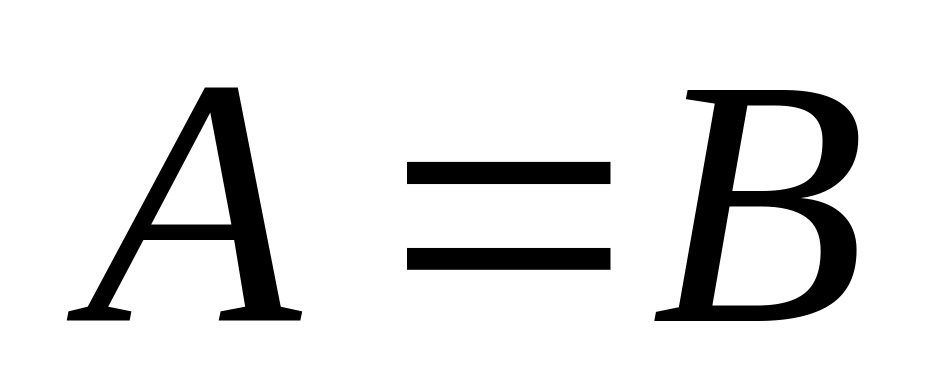 ).
).Объединением множеств А и В (обозначается
 )
называется множество, состоящее из
элементов, каждый из которых принадлежит
хотя бы одному из множеств. Кратко можно
записать следующим образом:
)
называется множество, состоящее из
элементов, каждый из которых принадлежит
хотя бы одному из множеств. Кратко можно
записать следующим образом:
 .
.Пересечением множеств А и В (обозначается
 )
называется множество, состоящее из
элементов, каждый из которых принадлежит
множеству А и множеству В. Кратко:
)
называется множество, состоящее из
элементов, каждый из которых принадлежит
множеству А и множеству В. Кратко:
 .
.Разностью множеств А и В (обозначается
 )
называется множество, состоящее из
элементов, каждый из которых принадлежит
множеству А и не принадлежит множеству
В. Кратко:
)
называется множество, состоящее из
элементов, каждый из которых принадлежит
множеству А и не принадлежит множеству
В. Кратко:
 .
.
В дальнейшем при изложении будем использовать следующие символы:
![]() –
–
![]() влечет
влечет
![]() ;
;
![]() –
и
равносильны;
–
и
равносильны;
![]() – «для
всякого», «для любого»;
– «для
всякого», «для любого»;
![]() – «существует»,
«найдется»;
– «существует»,
«найдется»;
: – «такое что».
8.2. Числовые множества
Одним
из основных понятий математики является
число. В курсе высшей математики мы
будем изучать, в основном, числовые
множества. Понятие числа возникло в
древности и на протяжении длительного
времени подвергалось расширению и
обобщению. Первые представления о числе
возникли из счета предметов. Результатом
счета являются числа 1,2,3,…. Такие числа
называются натуральными
и обозначаются N.
На языке множеств можно записать
следующим образом: N={1,2,3,…}.
Натуральные числа, противоположные
числа и 0 образуют множество
целых
чисел: Z={0,1,-1,2,-2…}.
К рациональным
числам
относят числа вида
![]() ,
где
,
где
![]() ,
т.е.
,
т.е.
![]() ={
:
}.
Все бесконечные непериодические дроби
образуют множество
иррациональных чисел.
Множество
действительных чисел
={
:
}.
Все бесконечные непериодические дроби
образуют множество
иррациональных чисел.
Множество
действительных чисел
![]() содержит все рациональные и иррациональные
числа, т.е. является объединением двух
множеств. Множество
можно изобразить в виде числовой оси,
где каждая точка является изображением
только одного действительного числа.
Множествами на такой числовой оси
являются следующие числовые промежутки
(здесь
содержит все рациональные и иррациональные
числа, т.е. является объединением двух
множеств. Множество
можно изобразить в виде числовой оси,
где каждая точка является изображением
только одного действительного числа.
Множествами на такой числовой оси
являются следующие числовые промежутки
(здесь
![]() ):
):
Замкнутый
интервал (отрезок)
![]() ;
;
Открытый
интервал
![]() ;
;
Полуоткрытые
интервалы
![]()
![]()
Полубесконечные
интервалы
![]()

Бесконечный
интервал
![]() .
.
Окрестностью точки
 называется любой интервал (a,b),
содержащий точку
.
В частности интервал
называется любой интервал (a,b),
содержащий точку
.
В частности интервал
 , где
, где
 называется
называется
 окрестностью
точки
.
окрестностью
точки
.
Далее приведем некоторые понятия, которые будут использоваться нами при изложении.
Абсолютной величиной (или модулем) действительного числа x называется неотрицательное число
 ,
определяемое соотношением
,
определяемое соотношением

Геометрически
выражает расстояние на числовой прямой
от точки 0 до точки х.
Соответственно,
![]() выражает расстояние от точки а
до точки х.
В частности,
окрестность
точки
можно описать неравенством
выражает расстояние от точки а
до точки х.
В частности,
окрестность
точки
можно описать неравенством
![]() .
.
Приведем без доказательства следующие свойства абсолютной величины:
 ; 2)
; 2)
 ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
 ,
если |y|0.
,
если |y|0.
Переменной величиной называется величина, которая принимает различные численные значения.
Совокупность всех числовых значений переменной величины называется областью изменения этой величины.
