Выявление и устранение случайных промахов

Если результат измерения существенно выходит за пределы доверительного интервала – его считают промахом. Промахом называют результат измерения, вероятность появления которого пренебрежимо мала. Такие результаты при обработке отбрасываются, так как их появление, скорее всего, связано со сбоем в работе аппаратуры или с ошибкой экспериментатора. Для того чтобы удостовериться в этом, производят дополнительные повторные измерения.

Выявление промахов производят путем сравнения погрешности результата отдельного измерения с доверительным интервалом. Если погрешность (отклонение от среднего) не укладывается в доверительный интервал – этот результат считают промахом и исключают. Однако, если погрешность не укладывается в доверительный интервал, то результат измерения может и не являться промахом.

Исторический пример. При исследовании Резерфордом свойств рассеяния  - частиц на тонких листах металлической фольги было установлено, что - частицы отклоняются на небольшие углы в 2 – 3 градуса и распределение частиц по углам соответствует кривой нормального распределения. Резерфорд произвел 100000 опытов. Было замечено, что некоторые частицы (1 на 8000) отклонялись на очень большие углы. Из статистических соображений эти результаты можно было отбросить как промахи... Большие углы отклонения впоследствии были объяснены ядерным взаимодействием  - частиц.

Практический критерий для выявления и устранения случайных промахов с учетом числа повторных измерений n:

если n<6 – ни один из результатов измерений нельзя считать промахом;

если 6<n<100 – промахом считается

S вычисляется без Y_i, подозреваемого как промах.

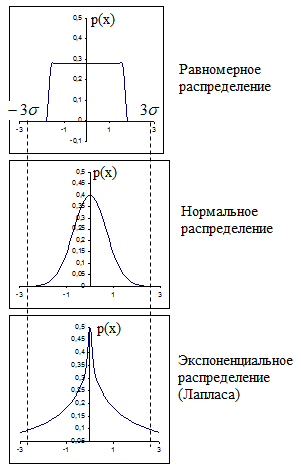
Примечание. Приведенный практический критерий для выявления случайных промахов безусловно применим в том случае, если закон распределения погрешности - нормальный. Действительно, для нормального распределения при n=>100 появление >3 можно считать промахом (см. рис 8б).

Для равномерного же распределения (рис. 8а) промахом является уже отсчет x_i, если >1,8. А для экспоненциального распределения Лапласа (рис. 8в) отсчет x_i, для которого = 3, безусловно принадлежит данной выборке и не может являться промахом.

Рис. 8

При компьютерной обработке данных описанная выше статистическая обработка может быть выполнена в программе Excel или в других программах цифровой обработки данных. Например, в библиотеке Advansed Analysis Library пакета LabWindows/CVI, предназначенного для предварительного анализа данных в режиме on-line, в классе функций статистической обработки (Statistics) содержатся следующие функции обработки массивов данных:

• Mean – вычисления среднего значения;

• StdDev – вычисления СКО;

• Variance – вычисления дисперсии;

• RMS – вычисления среднеквадратического значения;

• Moment – вычисления центральных моментов n-го порядка;

• Median – вычисления медианы;

• Mode – вычисления моды (наиболее часто встречающегося значения в массиве);

• Histogram – нахождения гистограммы;

• Sort – выполнения сортировки массива по возрастанию или убыванию.

Еще более широкий спектр функций статистической обработки предоставлен в MATLAB .

Систематическая и случайная погрешности.

Отличия в интерпретации результатов измерений.

Поле допуска систематической погрешности обозначает зону, в которой находится истинное значение измеряемой величины. Это означает, что аппроксимирующая кривая Y=f(X) не обязательно должна проходить по центру этой зоны. Можно лишь утверждать, что она проходит внутри этой зоны (рис.9а).

Поле допуска (доверительный интервал) случайной погрешности обозначает зону, в которой с определенным уровнем вероятности будут лежать результаты измерений.

Истинные значения измеряемой величины находятся в центральной части поля допуска. Истинному значению Y при каком-либо значении X соответствует математическое ожидание (МО) результатов повторных измерений. Погрешность определения МО по результатам ограниченного количества повторных измерений оценивается через среднеквадратическое отклонение математического ожидания (СКО МО).

и доверительный интервал математического ожидания

Таким образом, аппроксимирующая кривая Y=f(X) должна проходить по центру доверительного интервала случайной погрешности в пределах более узкого доверительного интервала математического ожидания (рис.9б).

А Б

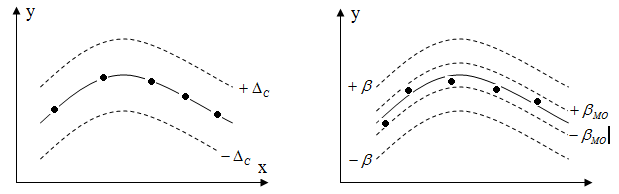
Рис. 9

Выбор количества повторных измерений при наличии как случайной, так и систематической погрешностей.

Доверительную погрешность результата повторных измерений вычисляют по формуле

где

У величивая количество повторных измерений, можно уменьшать случайную составляющую погрешности, т.к. она равна доверительному интервалу математического ожидания:

Суммарная погрешность при увеличении числа n вначале будет быстро уменьшаться, но при дальнейшем уменьшении n будет стремиться к величине _систпоэтому не имеет смысла брать очень большое количество повторных измерений. Практически рекомендуется [6] выбирать n из условия:

При выполнении этого условия величина доверительного интервала математического ожидания будет меньше систематической составляющей в 8 раз, поэтому случайная составляющая погрешности практически не будет влиять на точность измерений.

О тсюда рекомендуемая величина n вычисляется по формуле:

Контрольные вопросы и задачи

1. Приведите пример методической погрешности.

2. Приведите пример инструментальной погрешности.

3. В результате проведенной калибровки методом образцовых сигналов была получена зависимость Y=a+bX_эт . Каким образом производить восстановление значений измеряемого сигнала в ходе рабочего измерения?

4. В результате проведенной калибровки методом образцовых приборов была получена зависимость Y=a+bY_оп . Каким образом производить восстановление значений измеряемого сигнала в ходе рабочего измерения?

5. При определении центров распределений были получены следующие 5 оценок: 1.0 0.9 1.3 0.8 1.4. Рассчитайте значение центра распределения для случаев: а) случайная погрешность распределена по нормальному закону и промахов нет; б) случайная погрешность распределена по нормальному закону, но, возможно, есть промахи; в) случайная погрешность распределена по равномерному закону и промахов нет; г)случайная погрешность распределена по экспоненциальному закону; д)закон распределения случайной погрешности неизвестен; е) случайная погрешность распределена по двухмодальному закону.

6. При каком законе распределения погрешности результат измерения, отклоняющийся от среднего на а) 3,1σ; б) 2σ; в) 3σ можно (нельзя) считать промахом?

7. В таблице, приведенной ниже, представлены результаты эксперимента (6 опытов, по 20 повторных измерений в каждом опыте) и обработки. Найдите промахи.

Табл. 3

Лабораторная работа. Обработка результатов эксперимента.

Целью лабораторной работы является изучение методики статистической обработки результатов однофакторного эксперимента, включающей определение центров распределения в каждом опыте, оценку доверительного интервала погрешности, нахождение промахов, проверку однородности дисперсий.

Задание к работе

Имеется набор экспериментальных данных в табличной форме (6 опытов, 21 повторное измерение в каждом опыте).

Табл. 4

X	0	1	2	3	4	5
Y1	1,620006	2,398803	3,17768	4,565646	5,848881	6,96382
Y2	1,347202	2,676257	3,147425	4,012793	5,542281	6,054967
Y3	1,279479	2,840262	3,184779	4,056407	5,255239	6,691837
Y4	1,359743	2,768042	3,443239	4,793223	5,61322	6,601937
Y5	1,156957	2,03836	3,9041	4,273763	5,450143	6,728921
Y6	1,529537	2,21994	3,302557	4,960281	5,752975	6,423335
Y7	1,359152	2,640081	3,318498	4,173545	5,420599	6,300934
Y8	1,585824	2,277009	3,357476	4,410391	5,78365	6,308756
Y9	1,265405	2,975282	3,685053	4,877784	5,776524	6,300029
Y10	1,338051	2,280763	3,099172	4,520168	5,266072	6,923868
Y11	1,702966	2,936143	3,637146	4,664229	5,157994	6,52081
Y12	1,20397	2,360155	3,086753	4,337659	5,076156	6,872951
Y13	1,685963	2,759775	3,057118	4,730663	5,119084	6,119781
Y14	1,355981	2,110996	3,586492	4,12774	6,353788	6,894567
Y15	1,941773	2,923434	3,586826	4,253815	5,280676	6,484041
Y16	1,470065	2,499917	3,326187	4,174861	5,406829	6,995469
Y17	1,639323	2,666867	3,503163	4,084493	5,998003	6,802948
Y18	1,448085	2,453673	3,782372	4,098427	5,638602	6,603444
Y19	1,760679	2,418635	3,904236	4,47927	5,371588	6,649387
Y20	1,854512	2,916979	3,882532	4,893568	5,262242	6,863441
Y21	1,32304	2,24243	3,951743	4,084708	5,593404	6,025715

Требуется:

1. Найти центры распределений.

2. Определить доверительный интервал погрешности в каждом опыте.

3. Найти промахи.

4. Проверить выполнение условия однородности дисперсий в опытах по критерию Фишера.

Указания к выполнению работы

1. При нахождении центров распределения построить вариационные ряды во всех столбцах данных (Data/Sort), вычислить все 5 оценок (среднее арифметическое (функция AVERAGE), среднее арифметическое по 90% наблюдений, центр размаха, медиану, полусумму квантилей). Для вычисления полусуммы квантилей построить интервальную гистограмму распределения результатов измерений.

Построение интервальной гистограммы распределения результатов измерений производить средствами MS Excel в следующей последовательности:

1. Установить Пакет анализа: Tools/Add Ins/Analyses ToolPak.

2.Вызвать Пакет анализа: Tools/Data Analyses/Histogram

3. Внести во всплывающую панель рис. 10 условия построения гистограммы:

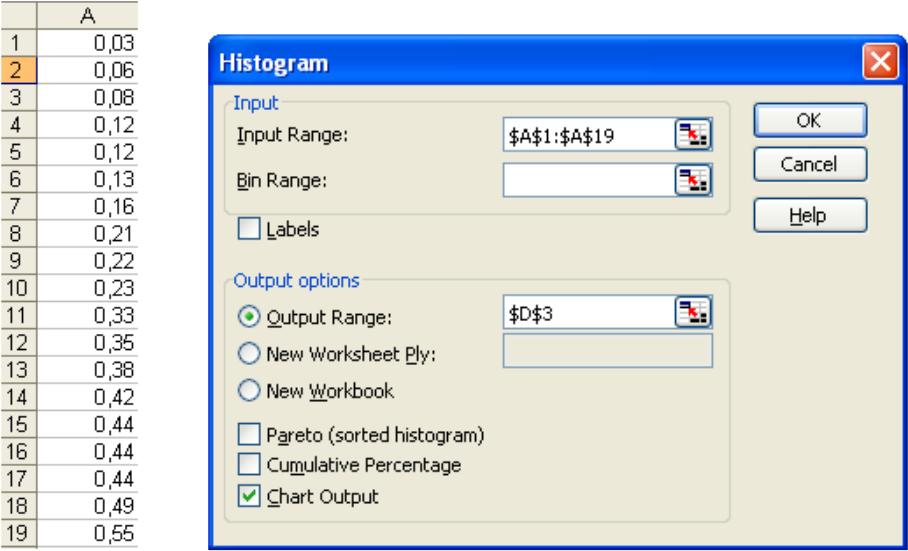
Рис. 10

Для нахождения 25 и 75-процентные квантилей могут быть использованы функции вычисления первого и третьего квартилей: QUARTILE(array,1) и QUARTILE(array,3), где array – числовой массив.

2. Для нахождения результирующей оценки центров распределения в каждом опыте скопировать таблицу значений центров распределения (Copy/Paste Special/Values), затем построить вариационный ряд оценок и в качестве результирующей оценки выбрать среднюю в вариационном ряду.

3. Для вычисления среднеквадратического отклонения в каждом опыте использовать функцию STDEV.

4. При вычислении доверительного интервала погрешности уровень доверительной вероятности принять равной 0,95.

5. Для нахождения промахов по вычисленным значениям доверительного интервала погрешности использовать операцию условного форматирования:

[Format] – [Condition Formatting], помечая столбцы таблицы с данными и выделяя с помощью условного форматирования другим цветом значения, лежащие в пределах доверительного интервала.

6. Для проверки однородности дисперсий вычислить отношение максимальной дисперсии к минимальной и сравнить с табличным значением коэффициента Фишера. Табличное значение взять для количества степеней свободы числителя и знаменателя равного n-1, т.е. 20.

Содержание отчета

1. Задание к работе.

2. Таблица исходных данных.

3. Рассчитанные значения 5-ти оценок центров распределения в каждом опыте.

4. Интервальные и кумулятивные гистограммы погрешностей.

5. Таблица центров распределения, расположенных в порядке возрастания.

6. График аппроксимирующей функции, построенный по центрам распределений.