Проектирование аппаратных средств измерения и управления

С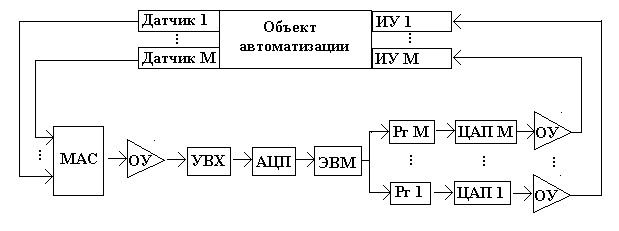 труктура подсистемы ввода/вывода аналоговых сигналов может быть представлена в виде рис. 85.

Рис. 85. МАС-мультиплексор аналоговых сигналов, ОУ-операционный усилитель, УВХ –устройство выборки/хранения.

В цифровой системе измерения и управления, содержащей АЦП в канале измерения, при проектировании необходимо производить расчет шага квантования по уровню X и шаг дискретности по времени t (см. рис.86).

Рис. 86

Выбор шага квантования по уровню

Выбор шага квантования по уровню производится из условия достижения необходимой точности восстановления значений непрерывного измеряемого сигнала в ЭВМ по дискретным отсчетам.

П огрешность восстановления может быть оценена максимальной и среднеквадратической ошибкой

учитывая, что закон распределения ошибки квантования – равномерный.

Исходя из уровня допустимой погрешности восстановления, условие выбора шага квантования по уровню можно записать в виде

У словие оптимального выбора шага квантования при котором и младший разряд АЦП несет полезную информацию

В ыбор шага квантования в диапазоне Xmin – Xmax определяет разрядность АЦП. Количество уровней квантования N АЦП в диапазоне изменения входного сигнала X_min – X_max равно

а количество разрядов выходного кода

n=log₂N

Расчет интервала дискретности по времени t.

Р асчет интервала дискретности по времени производится из условия достижения необходимой точности восстановления значений непрерывного сигнала по дискретным отсчетам в промежутках между отсчетами, при

Погрешность восстановления зависит от характера непрерывного сигнала X(t) и от используемого способа восстановления. Для восстановления используются интерполяционные и фильтрационные способы. Наиболее часто используется восстановление по теореме Котельникова , ступенчатая, линейная и кубичная сплайн-интерполяция.

а)восстановление по теореме Котельникова

В теореме Котельникова доказывается, что непрерывный сигнал может быть восстановлен абсолютно точно по дискретным отсчетам. Условия восстановления:

• непрерывный сигнал имеет ограниченный частотный спектр;

• отсчеты взяты через равные интервалы времени;

• ч астота отсчетов превышает не менее, чем вдвое, максимальную частоту в спектре непрерывного сигнала

В осстановление значений непрерывного сигнала необходимо производить по формуле:

В результате каждому значению дискретизированного сигнала будет посталена в соответствие функция типа интегрального синуса (см. примеры на рис. 87 и 88).

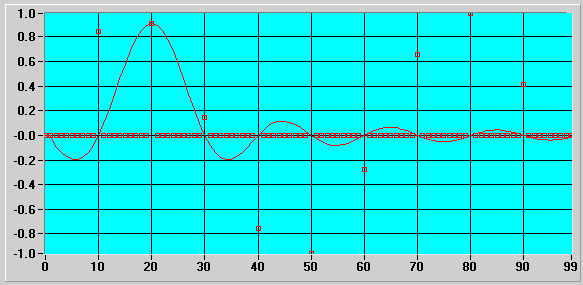
Рис. 87

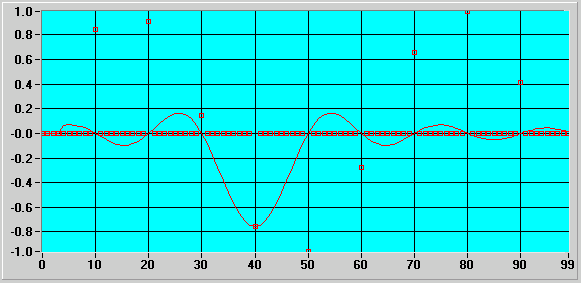
Рис. 88

После суммирования таких функций получим точное восстановление исходного непрерывного сигнала по дискретным отсчетам (см. рис. 89 и 90).

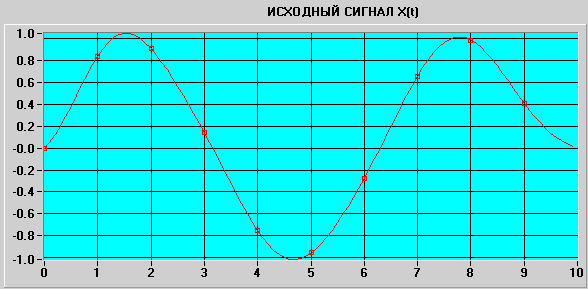
Рис. 89

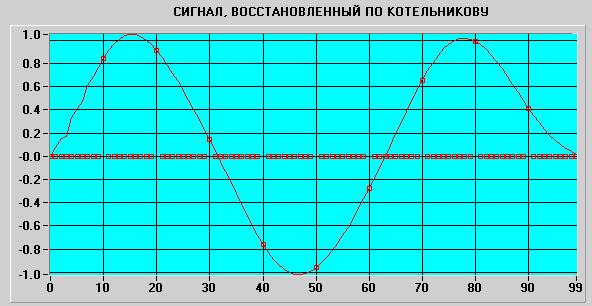
Рис. 90

Реализовать абсолютно точное восстановление непрерывного сигнала по дискретным отсчетам с использованием теоремы Котельникова, однако, невозможно по следующим причинам:

• Сигналы, ограниченные во времени, имеют бесконечный частотный спектр;

• Значения X(*t) известны с погрешностью.

б) с помощью ступенчатой интерполяции

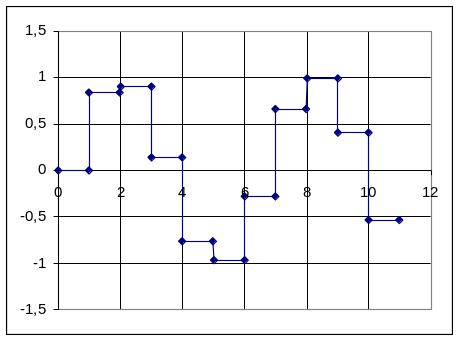
Рис. 91

При использовании ступенчатой интерполяции восстановление непрерывного сигнала по дискретным отсчетам производится по формуле:

Погрешность восстановления может быть оценена величиной

Отсюда

Для гармонического сигнала

имеем:

Отсюда

в) с помощью линейной интерполяции.

Рис. 92

При использовании линейной интерполяции восстановление

непрерывного сигнала по дискретным отсчетам производится по формуле:

Погрешность восстановления можно оценить величиной остаточного члена разложения в ряд Тейлора:

Отсюда

Для гармонического сигнала

Отсюда

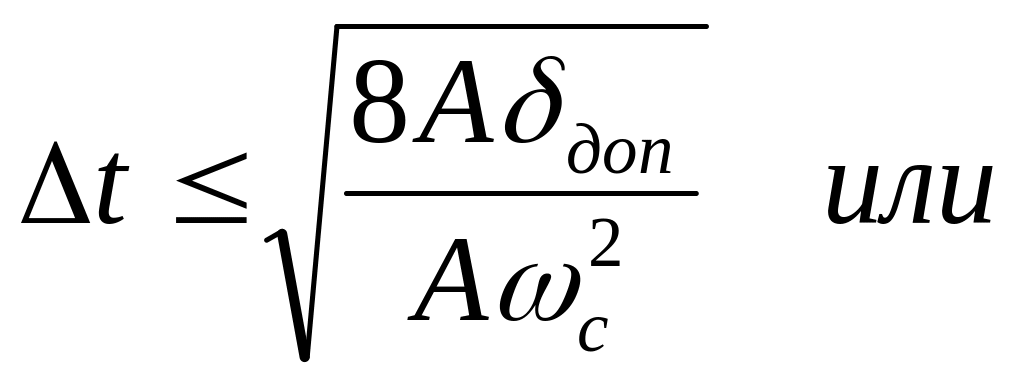
г) с помощью кубичной сплайн-интерполяции (в переводе spline означает «гибкая линейка»)

Попытка аппроксимации массива данных полиномом более высокой, чем вторая, степени не дает положительного результата. Однако если применить сплайновую интерполяцию, то картина кардинально меняется. На этот раз кусочная линия интерполяции прекрасно проходит через все точки. Даже ее пики воспроизводятся удивительно точно, причем и в случаях, когда на них не попадают узловые точки.

Причина столь великолепного результата кроется в уже отмеченных ранее особенностях сплайновой интерполяции - она выполняется по трем ближайшим точкам, причем эти тройки точек постепенно перемещаются от начала точечного графика функции к ее концу. Кроме того, непрерывность первой и второй производных при сплайновой интерполяции делает кривую очень плавной, что характерно и для первичной функции. Сплайн-интерполяция используется для представления данных отрезками полиномов невысокой степени — чаще всего третьей. При этом кубическая интерполяция обеспечивает непрерывность первой и второй производных результата интерполяции в узловых точках. Из этого вытекают следующие свойства кубической сплайн-интерполяции:

• график кусочно-полиномиальной аппроксимирующей функции проходит точно через узловые точки;

• в узловых точках нет разрывов и резких перегибов функции;

• благодаря низкой степени полиномов погрешность между узловыми точками обычно достаточно мала;

• связь между числом узловых точек и степенью полинома отсутствует;

• используется множество полиномов, появляется возможность аппроксимации функций с множеством пиков и впадин.

График интерполирующей функции при этом виде интерполяции можно уподобить кривой, по которой изгибается гибкая линейка, закрепленная в узловых точках.

Оценку погрешности при сплайн-интерполяции дает следующее утверждение:

Если интерполируемая функция f(x)  C⁴[a,b], то для функции погрешности R(x)=f(x)-g(x) справедливо неравенство:

где

Отсюда получаем условие выбора шага дискретности по времени:

Сравнение эффективности способов восстановления периодических сигналов

Для сравнения эффективности рассмотренных способов восстановления

полезно получить оценки соотношения частоты отсчетов f_отсч и максимальной частоты в спектре входного сигнала f_max

Сравнительную эффективность различных способов восстановления можно оценить по количеству отсчетов за период для типичных значений 1% и 0,1% погрешности восстановления (см. табл. 35)

Табл. 35

Погрешность восстановления	Ступенчатая интерполяция	Линейная интерполяция	Кубичная сплайн-интерполяция	По теореме Котельникова
1%	628	22	12	2
0,1%	6280	70	21	2

Э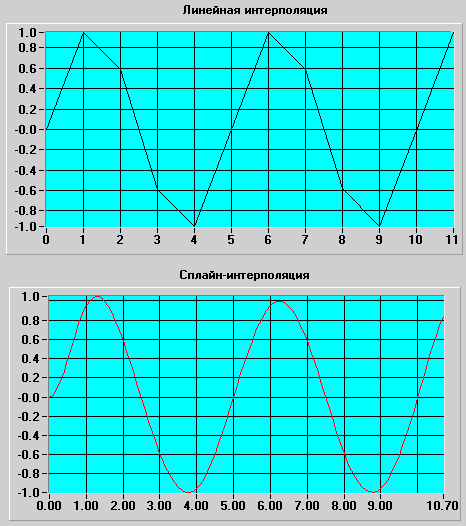 ти оценки показывают бесспорное преимущество способа восстановления по теореме Котельникова. Однако это преимущество будет возможным только для периодических сигналов, причем количество периодов должно быть достаточно велико.

Эффект существенного увеличения точности при переходе от линейной к сплайн-интерполяции иллюстрируется на рис. 93.

Рис. 93

Сравнение эффективности способов восстановления непериодических сигналов

Для непериодических сигналов типа косинусоидального и экспоненциального импульсов (см. рис. 94А,Б) получены следующие соотношения (см. Табл. 36).

А Б

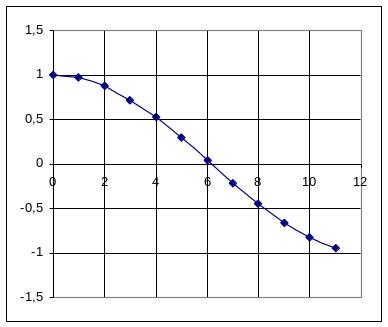
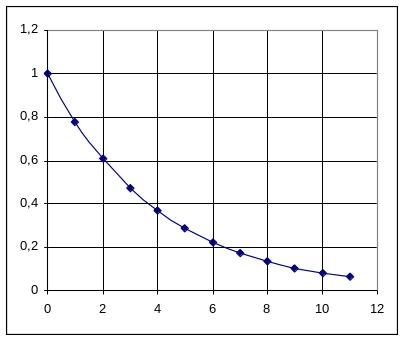
Рис. 94

Табл. 36. Количество отсчетов

Форма сигнала	Точность восстановления	Способ востановления
		По Котельникову	Ступенч. интерпол.	Линейная интерпол.
Косинусоид. импульс	0,1%	48	1570	18
	1%	16	156	7
Экспоненц. импульс	0,1%	200000	3000	35
	1%	2000	300	12

Контрольные вопросы и задачи

Требуется произвести расчет шага дискретности по времени для трех способов восстановления (с помощью ступенчатой интерполяции, линейной интерполяции, кубичной сплайн-интерполяции и по теореме Котельникова), времени цикла преобразования АЦП, шага квантования по уровню и количество разрядов выходного кода АЦП.

Табл. 37. Исходные данные для проектирования

Технические требования	Номер варианта исходных данных
	1	2	3	4	5
Тип датчика	Датчик давления «Сапфир»	Датчик давления МРХ2010	Датчик давления МРХ2050	Термопара типа К	Термопара ТПП13
Количество датчиков	3	4	4	1	1
Диапазон вых. сигналов датчика, мВ (мА)	0-20мА	0-25	0-40	0-5	0-50
Входное сопротивление канала измерения, кОм	0,25	1800	1000	1800	1800
Допустимая относительная погрешность измерения, %	0,1	0,1	0,1	0,2	0,2
F макс в спектре измеряемого сигнала, Гц	5	-	-	5	10
Максимальная скорость нарастания входного сигнала		0,05 мВ/мс	10 мВ/мс
Диапазон выходного сигнала, В	0-5	0-10	0-10	0-10	0-10
Выходное сопротивление, Ом	50	50	50	50	50
Частота выдачи выходного сигнала, кГц	1	4	2	8	1
Условия эксплуатации: диапазон температур, град	20	20	20	20	20

Табл. 38. Основные характеристики интегральных АЦП

Тип микросхемы	Диапазон входного сигнала, В	Кол-во разрядов выходного кода	Время цикла преобразования, мкс
К572ПВ1	0…10	12	110
К1107ПВ1	0…-2	6	0,1
К1107ПВ2	0…-2	8	0,1
К1107ПВ3	-2,5…+2,5	6	0,01
К1107ПВ4	-2,5…+2,5	8	0,03
К1107ПВ5	-2…+2	6	0,02
К1108ПВ1	0…+3	10	0,9
К1108ПВ2	-2,5…+2,5 0…5	12	2
К1113ПВ1	0…10,5 -5,5…+5,5	10	30

Литература

1. Ж. Макс. Методы и техника обработки сигналов при физических измерениях. В 2-х томах. М.: Мир, 1983,- 567с.

2. Х. Шенк. Теория инженерного эксперимента. М.: Мир, 1972,-381с.

3. И.А.Веренинов Автоматизация исследования движения тел в газовых средах на баллистических и плазмогазодинамических установках./ И.А.Веренинов, С.С.Попов, В.С.Тутыгин // В сб. У истоков космической эры / под ред. Ю.С.Васильева.— СПб. : Изд-во Политехн. ун-та. 2011.-158с.

4. П.А.Бутырин Автоматизация физических исследований и эксперимента. Компьютерные измерения и виртуальные приборы на основе LabView 7.0/ Бутырин П.А., Васьковская Т.А., Каратаев В.В., Маткрикин С.В. // М.: ДМК-Пресс 2011.

5. П.В.Новицкий, И.А.Зограф Оценка погрешностей результатов измерений. Л.: Энергоатомиздат. Ленингр. отд., 1991, - 301с.

6. В.Д.Мазин Планирование измерений и обработка результатов эксперимента: Учебное пособие. - СПб. : Изд-во Политехн. ун-та. 1992.-28с.

7. Е.И.Куликов Прикладной статистический анализ: Учебное пособие для вузов.- М.: Радио и связь. 2003.-376с.

8. В.А.Лунев. Основы научных исследований. Планирование и обработка технологического эксперимента: Учебное пособие. – СПб.:СПбГТУ, 1996.- 117с.

9. В.С.Тарасов Методы планирования и моделирования объектов эксперимента. Уч. пособие. –Л.: ЛПИ, 1986.-88с.

10. М. Гук Аппаратные интерфейсы ПК. Энциклопедия.- СПб.: Питер, 2003,

- 528 с.

11. А.Лапин. Интерфейсы. Выбор и реализация. М., Изд. «Техносфера», 2006, – 200с.

12. Фарзин А. Абедадзе, Чжу Ань, Ли Ден и др. Сопряжение датчиков и устройств ввода данных с компьютерами IBM PC. Под ред. У.Томпкинса и Дж.Уэбстера.-М.:Мир, 1992г.-579с.

13. Пей Ан. Сопряжение ПК с внешними устройствами. Пер. с англ. – М.:ДМК Пресс, 2001.-320с.

14. Ю.В.Новиков Разработка устройств сопряжения для персонального компьютера IBM PC./ Ю.В.Новиков , О.А.Калашников, С.Э.Гуляев // M., Изд. "Эком". 1998, - 221с.

15. Г.Олсон , Д.Пиани. Цифровые системы автоматизации и управления, СПб.: Невский диалект, 2001, 557с.

16. В.С.Тутыгин Основы автоматизации физического эксперимента. Лаб.практикум. СПб.: Изд-во Политехн. ун-та, 2008,- 69с.

1 Басаргин И.В., Мишин Г.И., Федотов А.А. Автоматизированная установка для исследования динамических свойств ударных волн в газоразрядной плазме. Препринт 1642 ФТИ им. А.Ф.Иоффе РАН.

2 Кондратьев Б.С. Статистический анализ флуктуаций тока микроплазм в высоковольтных кремниевых p-n структурах. / Кондратьев Б.С., Соболев Н.А., Тутыгин В.С., Тиранов М.Л.// Препринт 1252 ФТИ им. А.Ф.Иоффе РАН.

3 УСО – устройства сопряжения с объектом

4 Задание напряжения источника сигнала калибровки

5 Задание уровня синхронизации

6 В.П.Себко, Г.М.Сучков, Е.А.Алексеев. Оптимизация параметров ЭМА-толщиномеров для контроля тонкостенных изделий. - Дефектоскопия. 2002. № 12.

7 В.С.Тутыгин. Программа точного определения времени задержки радиолокационного эхо-сигнала. Свидетельство Роспатента об официальной Гос. регистрации №2011612678 от 01.04.2011. www1.fips.ru/Electronic_bulletin/Programs_db_topology/pr.pdf

8 API – (Application Program Interface) – интерфейс прикладных программ.

9 При программировании САМАС-операций в среде LabWindows/CVI 8.0 синтаксис операторов ввода/вывода другой. Должна использоваться библиотека camlib1.c

0