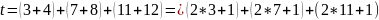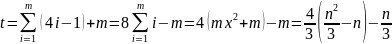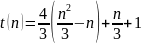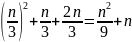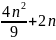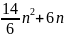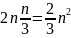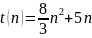- •Введение
- •Описание формальной модели алгоритма на основе рекурсивных функций
- •Аналитическая модель Машины Тьюринга
- •2.1 Элементарная Машина Тьюринга
- •2 Трассировка алгоритма на каком-то контрольном значении Рисунок 1 - Тестирование Машины Тьюринга .2 Композиция Машин Тьюринга
- •Распознающая Машина Тьюринга
- •3.1 Постановка задачи
- •2.3.2 Описание распознающей Машины Тьюринга
- •Аналитическая модель Нормальных алгоритмов Маркова
- •Заключение
- •Список ссылок
2 Трассировка алгоритма на каком-то контрольном значении Рисунок 1 - Тестирование Машины Тьюринга .2 Композиция Машин Тьюринга
Построить композицию Машин Тьюринга для вычисления ближайшего к s простого числа в унарном коде без сохранения исходных данных.
Пример входных данных: 111111
Пример выходных данных: 11111
Ниже привдена блок-схема алгоритма, реализующего вычисление заданного алгоритма:
<<<Блок-схема>>
Рисунок 1 - Блок схема алгоритма поиска ближайшего к s простого числа
В композиции будут участвовать следующие Машины Тьюринга:
 – машина копирования;
– машина копирования;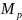 –
машина проверки на простоту;
–
машина проверки на простоту; – машина выбора m-го элемента из n;
– машина выбора m-го элемента из n;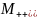 - машина увеличения на единицу;
- машина увеличения на единицу;
СХЕМА КОМПОЗИЦИИ ИЗ 3 ЛАБЫ
Рисунок 1 - Композиция Машин Тьюринга
- машина уменьшения на единицу.
Теперь распишем машину , которая используется для проверки числа на простоту.
В композиции будут участвовать машины:
– машина копирования;
– машина выбора m-го элемента из n;
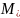 - машина логическое и;
- машина логическое и;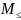 - машина
сравненения;
- машина
сравненения; - машина установки
двойки;
- машина установки
двойки;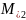 - машина проверки на равенство двойке;
- машина проверки на равенство двойке;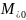 - машина проверки на равенство нулю;
- машина проверки на равенство нулю;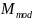 - машина вычисления остатка от деления;
- машина вычисления остатка от деления;- машина увеличения на единицу;
- машина уменьшения на единицу;
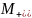 - машина сложения.
- машина сложения.
СХЕМА КОМПОЗИЦИИ ИЗ 3 ЛАБЫ
Рисунок 2.6 - Композиция машины проверки на простоту
Распознающая Машина Тьюринга
3.1 Постановка задачи
Необходимо реализовать распознающую Машину Тьюринга для определения принадлежности входного слова языку L = { www│w{0, 1}*}. Машина проверяет принадлежность слова языку и после него записывает символ “T”, если слово принадлежит языку и символ “F” - в противном случае.
Пример входных данных: 110110110
Пример выходных данных: 110110110T
2.3.2 Описание распознающей Машины Тьюринга
Таблица 1 - Таблица состояний
q\a |
1 |
0 |
λ |
3 |
2 |
$ |
5 |
4 |
# |
q0 |
|
|
|
|
|
|
|
|
|
q1 |
|
|
|
|
|
|
|
|
|
q2 |
|
|
|
|
|
|
|
|
|
q3 |
|
|
|
|
|
|
|
|
|
q4 |
|
|
|
|
|
|
|
|
|
q5 |
|
|
|
|
|
|
|
|
|
q6 |
|
|
|
|
|
|
|
|
|
q7 |
|
|
|
|
|
|
|
|
|
q8 |
|
|
|
|
|
|
|
|
|
q9 |
|
|
|
|
|
|
|
|
|
Продолжение таблицы 3.1
q\a |
1 |
0 |
λ |
3 |
2 |
$ |
5 |
4 |
# |
q10 |
|
|
|
|
|
|
|
|
|
q11 |
|
|
|
|
|
|
|
|
|
q12 |
|
|
|
|
|
|
|
|
|
q13 |
|
|
|
|
|
|
|
|
|
q14 |
|
|
|
|
|
|
|
|
|
q15 |
|
|
|
|
|
|
|
|
|
q16 |
|
|
|
|
|
|
|
|
|
q17 |
|
|
|
|
|
|
|
|
|
q18 |
|
|
|
|
|
|
|
|
|
q19 |
|
|
|
|
|
|
|
|
|
q20 |
|
|
|
|
|
|
|
|
|
q21 |
|
|
|
|
|
|
|
|
|
q22 |
|
|
|
|
|
|
|
|
|
q23 |
|
|
|
|
|
|
|
|
|
q24 |
|
|
|
|
|
|
|
|
|
В таблице 3.2 приведены комментарии, поясняющие назначение состояний:
Таблица 1 - Комментарии к состояниям Машины Тьюринга
Состояние |
Комментарий |
q0 |
|
q1 |
|
Продолжение таблицы 3.2
Состояние |
|
q2 |
|
q3 |
|
q4 |
|
q5 |
|
q6 |
|
q7 |
|
q8 |
|
q9 |
|
q10 |
|
q11 |
|
q12 |
|
Продолжение таблицы 3.2
Состояние |
|
q13 |
|
q14 |
|
q15 |
|
q16 |
|
q17 |
|
q18 |
|
q19 |
|
q20 |
|
Продолжение таблицы 3.2
Состояние |
|
q21 |
|
q22 |
|
q23 |
|
q24 |
|
На рисунке 3.1 приведено тестирование алгоритма распознающей машины:
Входные данные: 101010
Результат: 101010T
Рисунок 1 - Тестирование алгоритма
2.3.3 Временная сложность машиныНа рисунке 3.2 приведён график временной сложности выполнения алгоритма.

Рисунок 3.2 - График временной сложности
На графике видно, что функция сложности имеет два скачка в точках 3 и 6. Это обусловлено тем, что слова, длинна которых не кратна трём отсекаются ещё на первых этапах проверки, в то время как слова, кратные трём нуждаются в дополнительном исследовании. Притом, если слово кратно трем, но не является словом языка, машина закончит свою работу раньше, чем при обработке слова языка.
Для вычисления функции сложности рассмотрим такие входные данные: 110110110.
Головка будет двигаться вперёд (состояния 0, 1, 2) и пройдёт 3 шага, затем 4 шага назад. Второй проход: 7 шагов вперёд, 8 назад. Третий проход: 11 шагов назад, 12 вперёд. Можно заметить, что:
|
(1) |
Или в общем случае, для произвольного m — количества проходов (количество проходов равно длине слова (n), делённому на 3).
|
(1) |
Итого:
|
(1) |
|
(1) |
Для второй тройки:
|
(1) |
Так как троек три, то весь этап займёт:
|
(1) |
Прибавляя это значение к предыдущему, получим:
|
(1) |
После этого производятся проходы с целью проверки. На них тратится:
|
(1) |
Всего:
|
(1) |
Так как в некоторых местах этого расчёта использовались приближения, слагаемое 1 несущественно.
Это время выполнения для слова, принадлежащего языку. Рассмотрим теперь слова, не принадлежащие языку, длинна которых кратна 3.
……
Длина слова |
Теоретическая оценка |
Практическая оценка |
3 |
36 |
37 |
6 |
114 |
109 |
9 |
234 |
211 |
Следует отметить, что в случае ввода данных, не принадлежащих языку, программа сработает быстрее. Например, в случае ввода слова, длина которого не кратна трём, алгоритм сработает быстрее, чем (3.3).