Восстанавливаемая резервированная система с дробной кратностью при неограниченном ремонте с нагруженным резервом
Рис. 5 «Схема надежности восстанавливаемой резервированной системы с дробной кратностью при неограниченном ремонте с нагруженным резервом для конкретных значений количества резервных элементов»
На Рис. 5 элементы 1, 2 и 3 – основные, а элементы 4 и 5 – работают в режиме горячей замены.
Найдем вероятностные характеристики данной системы методом дифференциальных уравнений.
Для этого сначала построим вероятностный граф состояний (ВГС). За состояние примем количество неисправных элементов системы.
Рис. 6 «ВГС для восстанавливаемой резервированной системы с дробной кратностью при неограниченном ремонте с нагруженным резервом»
На основе ВГС, приведенного на Рис. 6, запишем систему дифференциальных уравнений:
Начальный условия для этой системы таковы:
Проведем для вышеприведенной системы уравнений в пакете Maple 7 прямое преобразование Лапласа. В результате получим следующую систему:
Решим полученную системы линейный уравнений в пакете Maple 7. В результате получим:
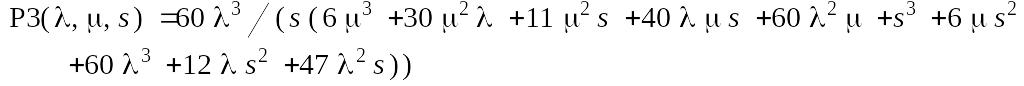
Для полученных выражений проведем в пакете Maple 7 обратное преобразование Лапласа. В результате получим:
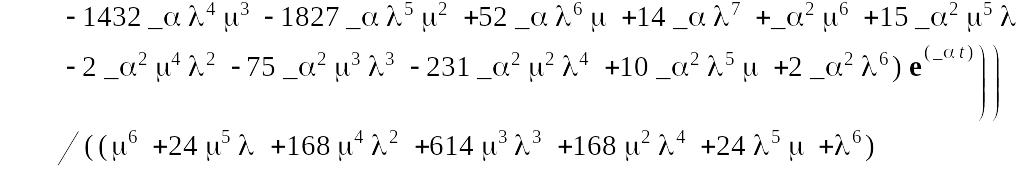
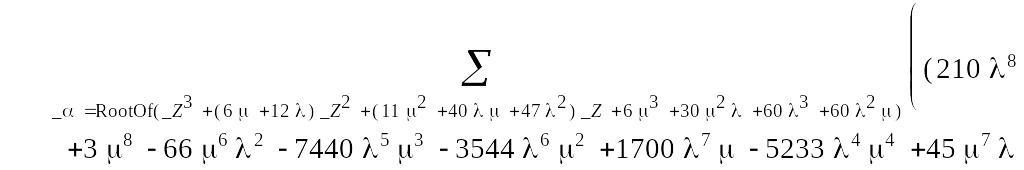
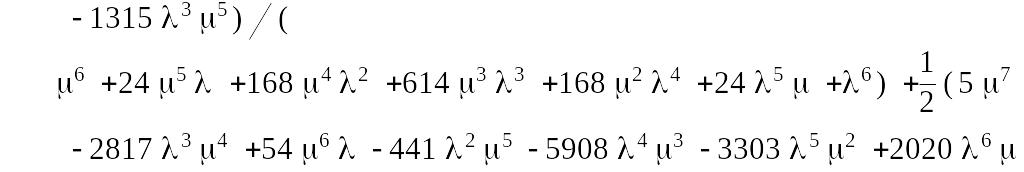
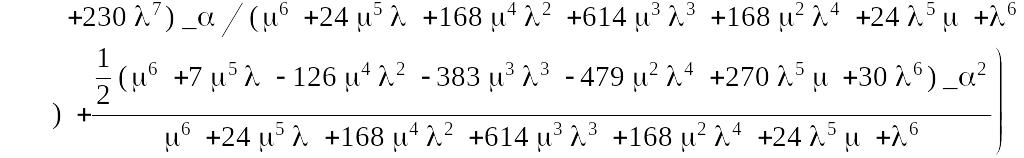
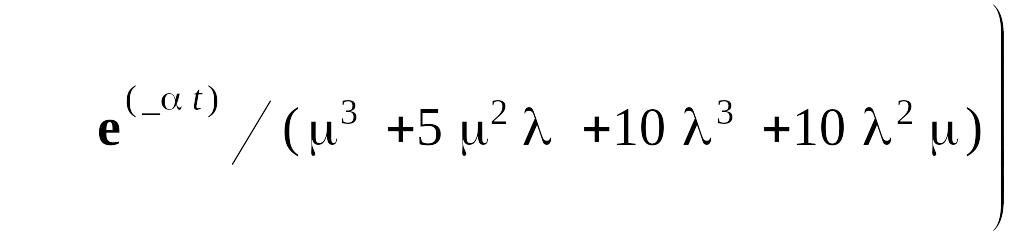
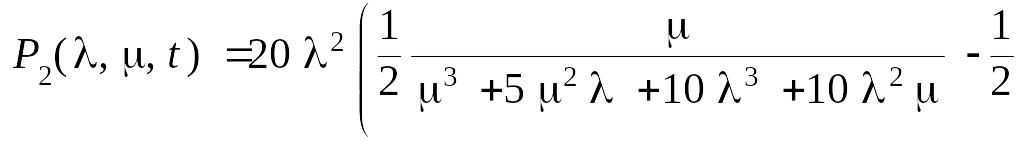
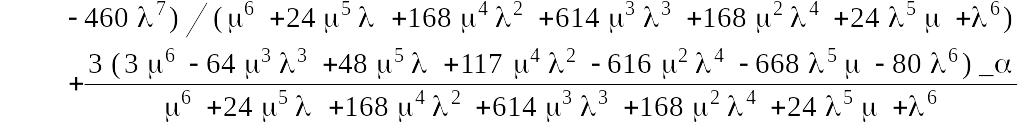
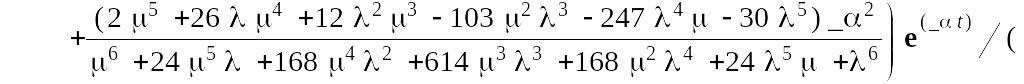
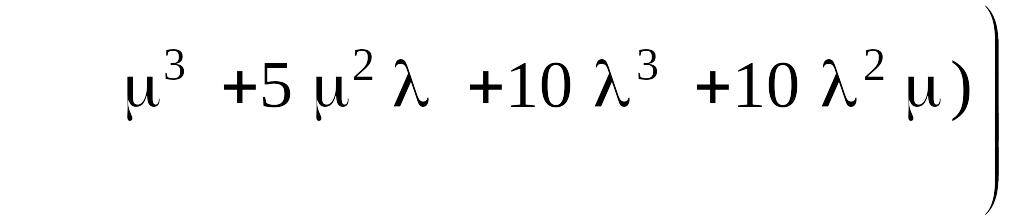
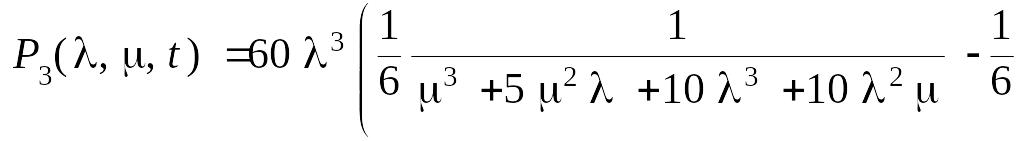
Вероятность безотказной работы системы равна:
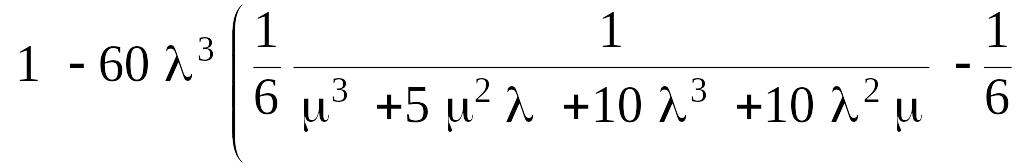
Среднее время наработки системы на отказ в установившемся режиме рассчитывается как:
Среднее время восстановления системы в установившемся режиме рассчитывается как:
Коэффициент готовности равен:
Вероятность успешного использования системы рассчитывается по формуле:
С ненагруженным резервом
Рис. 7 «Схема надежности восстанавливаемой резервированной системы с дробной кратностью при неограниченном ремонте с ненагруженным резервом для конкретных значений количества резервных элементов»
На Рис. 7 элементы 1, 2 и 3 – основные, а элементы 4 и 5 – работают в режиме холодной замены.
Найдем вероятностные характеристики данной системы методом дифференциальных уравнений.
Для этого сначала построим вероятностный граф состояний (ВГС). За состояние примем количество неисправных элементов системы.
Рис. 8 «ВГС для восстанавливаемой резервированной системы с дробной кратностью при неограниченном ремонте с ненагруженным резервом»
На основе ВГС, приведенного на Рис. 8, запишем систему дифференциальных уравнений:
Начальный условия для этой системы таковы:
Проведем для вышеприведенной системы уравнений в пакете Maple 7 прямое преобразование Лапласа. В результате получим следующую систему:
Решим полученную системы линейный уравнений в пакете Maple 7. В результате получим:
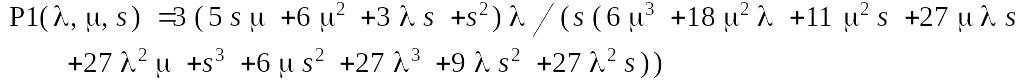
Для полученных выражений проведем в пакете Maple 7 обратное преобразование Лапласа. В результате получим:
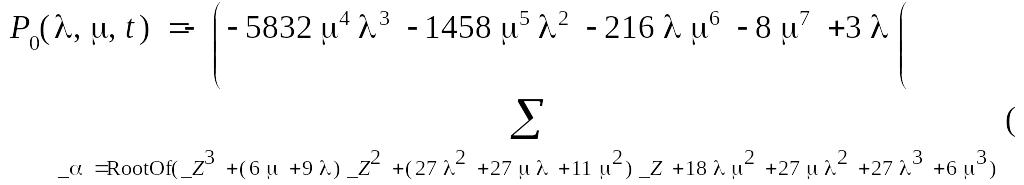
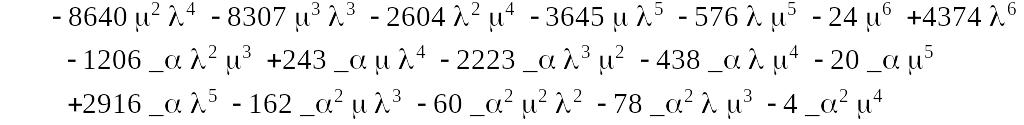
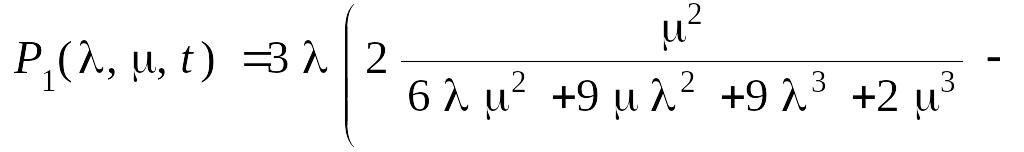
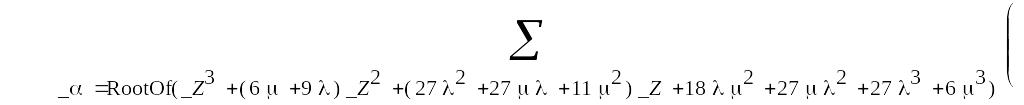
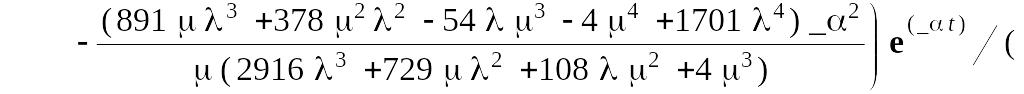
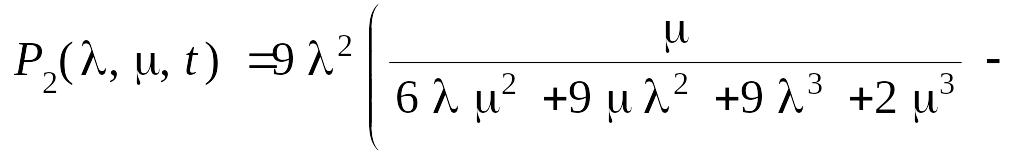
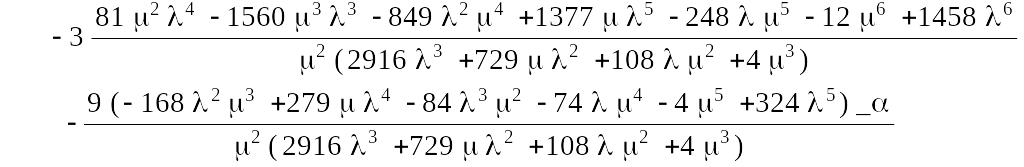
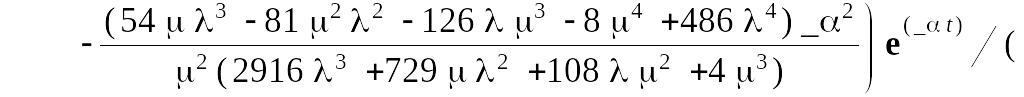
Вероятность безотказной работы системы равна:
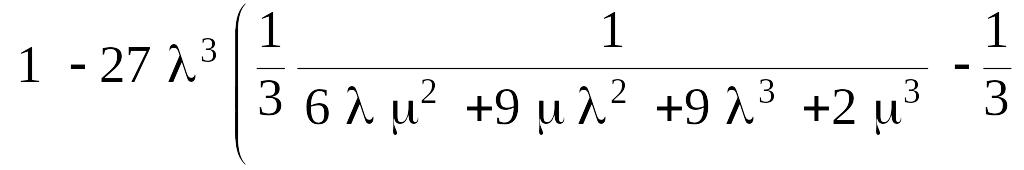
Среднее время наработки системы на отказ в установившемся режиме рассчитывается как:
Среднее время восстановления системы в установившемся режиме рассчитывается как:
Коэффициент готовности равен:
Вероятность успешного использования системы рассчитывается по формуле: