Экстремумы функции
Определение 6. Функция y = f(x) имеет в точке x0ÎD(f) максимум ymax (минимум ymin), если существует такая окрестность точки x0, в которой для всех x выполняется неравенство:
f(x0) > f(x) (f(x0) < f(x)).
Определение 7. Точки максимума и минимума функции называются точками экстремума функции.
Теорема 3 (необходимое условие экстремума). Если функция y = f(x) имеет экстремум в точке x0, то в этой точке производная функции равна нулю или не существует.
Доказательство. 1)Для определённости рассмотрим случай, когда функция y = f(x) в точке x0 имеет максимум и в этой точке существует производная. Тогда из определения максимума для любого x, принадлежащего окрестности точки x0 f(x0) > f(x).
Отсюда следует, что для любого x ≠ 0 справедливо неравенство: f(x0+x) – f(x0) < 0. Разделим это неравенство на Dx, получим:
при Dx
> 0:
при Dx
< 0:
Перейдём к пределам:
Так
как
существует, то:
Аналогично рассматривается случай, когда x0 – точка минимума.
2) Если f '(x0) не существует или равна ¥, то точка x0 может быть точкой экстремума функции.
Например, функция y =
имеет минимум при x
= 0, хотя y'(0) не
существует (рис. 9).
Рис. 9
Теорема доказана.
Теорема 4 (достаточное условие экстремума). Если функция y = f(x) непрерывна в точке x0, дифференцируема в некоторой её окрестности, за исключением может быть самой этой точки, f’(x0) = 0 или не существует и при переходе x через точку x0 производная f '(x) изменяет знак, то точка x0 является точкой экстремума. Если при этом знак f '(x) меняется
с + на –, то x0 – точка максимума,
с – на +, то x0 – точка минимума.
Доказательство. Пусть f '(x) при переходе x через точку x0 изменяет знак с
+ на – , т.е. f '(x) > 0 при x Î (x0 – ; x0) и f '(x) < 0 при x Î (x0; x0 + ), где > 0 (рис. 10).
Рис. 10
1) Пусть x Î (x0 – ; x0). На отрезке [x; x0] функция y = f(x) удовлетворяет теореме Лагранжа. Значит, на интервале (x; x0) найдётся хотя бы одна точка c1, в которой выполняется равенство:
f(x) – f(x0) = f '(c1)(x – x0),
где c1 (x0 – ; x0).
Так как f '(c1) > 0 и x – x0 < 0, то f(x) – f(x0) < 0.
2) Пусть
.
На отрезке
функция
также удовлетворяет теореме Лагранжа.
Значит на интервале (x0;
x) найдётся хотя бы
одна точка с2, в которой
выполняется равенство:
f(x) – f(x0) = f’(c2)(x – x0),
где c2 (x0; x0 + ).
Так как f '(c2) < 0 и x – x0 > 0, то f(x) – f(x0) < 0.
Следовательно, для любого x Î (x0 – d; x0 + d) выполняется неравенство:
f(x0) > f(x).
Отсюда следует, что точка x0
является точкой максимума функции
y = f(x).
Аналогично рассматривается случай,
когда
при
переходе x через точку
x0 изменяет знак
с – на +. При этом точка x0
является точкой минимума
функции
.
Теорема доказана.
Выпуклость, вогнутость и точки перегиба графика функции
Пусть функция y = f(x) дифференцируема в любой точке промежутка (a;b). Тогда она имеет конечную производную в любой точке этого промежутка. Значит, существует касательная к графику функции y = f(x) в любой его точке (x; f(x)) при a < x < b.
Определение 8. График функции y = f(x), дифференцируемой в каждой точке промежутка (a;b), называется выпуклым (вогнутым) на этом промежутке, если для любого x Î (a;b) график расположен не выше (не ниже) касательной к графику в точке (x; f(x)).
Теорема 5 (достаточное условие выпуклости или вогнутости кривой).
Пусть функция y = f(x) дважды дифференцируема на промежутке (a;b) и f ''(x) для x Î (a;b) сохраняет свой знак, тогда кривая y = f(x) выпуклая, если f ''(x) 0
при x Î (a;b), и кривая y = f(x) вогнутая, если f ''(x) 0 при x Î (a;b).
Доказательство. Для определённости рассмотрим случай, когда f ''(x) 0 для x Î (a;b). Обозначим x0 любую точку промежутка (a;b). Построим касательную к кривой y = f(x) в точке (x0; f(x0)): yкасат = f(x0) + f '(x0)∙(x – x0). Покажем, что график функции y = f(x) лежит не ниже этой касательной,
т.е. выполняется неравенство: (f(x) – yкасат(x)) 0 для любого x Î (a;b) (рис.11).
f(x) – yкасат(x) = f(x) – (f(x0) + f '(x0)∙(x – x0)) =
= f(x) – f(x0) – f '(x0)∙(x – x0) = (f(x) – f(x0)) – f '(x0)∙(x – x0), (1)
где x Î (a;b) .
Функция y = f(x) на отрезке [x0;x] удовлетворяет условию теоремы Лагранжа, т.е. на отрезке [x0;x] найдётся хотя бы одна точка c1, для которой
выполняется равенство:
f (x) – f(x0) = f '(c1)∙(x – x0).
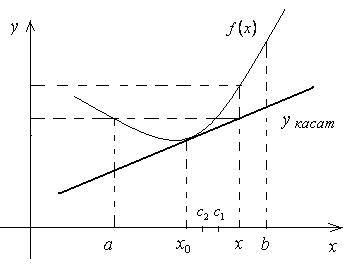
Рис. 11
Подставим в равенство (1) полученное соотношение.
f(x) – yкасат(x) = f '(c1)(x– x0) – f ' (x0)(x – x0) = (x – x0)(f ' (c1) – f ' (x0)). (2) Функция f '(x) на отрезке [x0;c1] удовлетворяет условию теоремы Лагранжа, т.е. на промежутке (x0;c1) найдётся хотя бы одна точка с2, для которой выполняется равенство:
f '(c1) – f '(x0) = f ''(c2)(c1 – x0).
Подставим в равенство (2) полученное соотношение:
f(x) – yкасат(x) = (x – x0)f ''(c2)∙(c1 – x0). (3)
Если x > x0, то c1 > x0 и c2 > x0, т.е. x – x0 > 0 и с1 – x0 > 0.
По предположению f ''(x) 0. Тогда f(x) – yкасат(x) 0.
Если x < x0, то c1 < x0 и c2 < x0, т.е. x – x0 < 0 и c1 – x0 < 0. Тогда f(x) – yкасат(x) 0.
Следовательно, при любом x Î (a;b) выполняется неравенство:
f(x) – yкасат(x) 0,
т.е. на промежутке (a,b) график функции y = f(x) вогнутый.
Аналогично можно доказать, что если f ''(x) 0 при любом x Î (a;b), то кривая y = f(x) на промежутке (a;b) будет выпуклой.
Теорема доказана.
Определение 9. Пусть в точке (x0; f(x0)) существует касательная. Тогда точка (x0; f(x0)), отделяющая выпуклую часть кривой от вогнутой (или наоборот) называется точкой перегиба графика функции y = f(x).
Теорема 6 (достаточное условие точки перегиба). Если функция y = f(x) дважды дифференцируема в окрестности точки x0, вторая производная функции f ''(x0) = 0 (или не существует) и f ''(x) меняет свой знак при переходе x через точку x0, то точка (x0; f(x0)) – точка перегиба кривой y = f(x).
Доказательство. Для определенности рассмотрим случай, когда f ''(x) при переходе через точку x0 изменяет знак с + на –.
Тогда в левой полуокрестности точки x0 f ''(x) > 0, т. е. кривая при x < x0 вогнутая, а в правой полуокрестности точки x0 f ''(x) < 0, т. е. кривая при x > x0 выпуклая.
Следовательно, точка (x0; f(x0)) по определению является точкой перегиба графика функции y = f(x).
Аналогично рассматривается другой случай, когда f ''(x) при переходе
через точку x0 изменяет знак с – на +.
Теорема доказана.