Швидке сортування

В загальному алгоритм швидкого сортування можна описати так:

quickSort

• Вибрати опорний елемент p

• Розділити масив по цьому елементу (реорганізувати масив таким чином, щоб всі елементи, менші або рівні опорному, виявилися зліва від нього, а всі елементи, більші опорного, - справа від нього)

• Якщо підмасив зліва від p містить більше одного елемента, викликати quickSort для нього (тобто повторити рекурсивно для підмасиву зліва від р)

• Якщо підмасив справа від p містить більше одного елемента, викликати quickSort для нього (тобто повторити рекурсивно для підмасиву справа від р)

  Часто в якості опорного елемента пропонується вибрати медіану (середину масиву). Однак можна підібрати приклад, при якому алгоритм з вибором медіани в якості опорного елемента буде видавати неправильну відповідь. Відомі стратегії: вибирати постійно один і той самий елемент, наприклад, перший або останній; вибрати елемент випадковим чином.

Недолік вибору в якості опорного одного із крайніх елементів масиву — при передачі параметром уже відсортованого масиву такий вибір призводить до найгіршого випадку.

Недолік вибору опорного елемента випадковим чином — залежність швидкості алгоритму від реалізації генератора псевдовипадкових чисел. Якщо генератор працює повільно і видає погані послідовності псевдовипадкових чисел, можлива затримка роботи алгоритму. Оцінювання середньостатистичних значень M та C є нелегкою задачею з огляду на необхідність використання апарату теорії ймовірностей, але обидві величини будуть порядку ~ N log ₂ N.

Елементарні структури даних: Стеки, черги.

Математичні основи аналізу алгоритмів. Графи. Дерева.

Стеки та черги — це динамічні множини, елементи з яких видаляються за допомогою попередньо визначеної операції Delete.

Першим зі стеку (stack) видаляється елемент, який був поміщений туди останнім: в стеку реалізується стратегія «останнім зайшов — першим вийшов" (last-in, first-out — LIFO).

В черзі (queue) завжди видаляється елемент, який міститься в множині довше за інших: в черзі реалізується стратегія «першим зайшов - першим вийшов" (first-in, first-out — FIFO).

Реалізуємо обидві ці структури даних за допомогою звичайного масиву.

Операція додавання елемента в стек часто позначається Push (запис в стек), а операція видалення — Pop (зняття зі стеку).

Стек можна представити у вигляді стопки тарілок, з якої можна взяти верхню і на яку можна покласти нову тарілку.

Як видно з малюнку, стек, здатний вмістити не більше ніж n елементів, можна реалізувати за допомогою масиву S [1..n]. top [S] - індекс останнього елемента, який помістили в стек.

С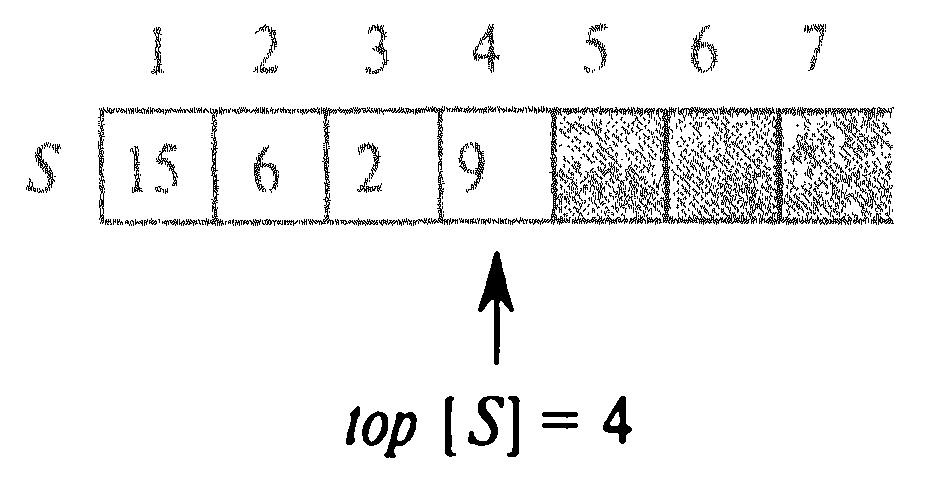 тек складається з елементів

S [1.. top [S]], де S [1] — елемент на дні стеку,

S [top [S]] — елемент на його вершині.

На малюнку елементи стека знаходяться тільки у світлих клітинках.

На малюнку а) зображений стек S, що складається з 4 елементів. На вершині стека знаходиться елемент 9.

На мал. б) представлений цей же стек після виклику процедур Push(S, 17) і Push(S, 3).

На мал. в) — після виклику процедури Pop(S), яка повертає вставлене в стек останнім значення 3. Не дивлячись на те, що елемент 3 все ще показаний в масиві, він більше не належить стеку; тепер на вершині стека — 17.

Будь-яка з описаних операцій зі стеком виконується протягом часу О(1).

Якщо top [S] = 0, то стек не містить жодного елементу і є пустим (empty). Протестувати стек на наявність в ньому елементів можна за допомогою операції-запиту Stack_Empty.

Якщо елемент знімається з пустого стеку, то говорять, що він спустошується (underflow), що зазвичай призводить до помилки.

Якщо значення top [S] більше n, то стек переповнюється (overflow).

(В представленому нижче псевдокоді можливе переповнення до уваги не береться.)

Операції зі стеком (перевірка на порожність, додавання елемента, видалення елемента) записуються так:

Stack_Empty(S)

1 if top[S]=0

2 then return TRUE

3 else return FALSE

Push(S, x)

1 top[S]<-top[S]+1

2 S[top[S]]<-x

Pop(S)

1 if Stack_Empty(S)

2 then error “underflow”

3 else top[S]<-top[S]-1

4 return S[top[S]]+1]

Черги

Операцію додавання елемента до черги будемо називати Enqueue (помістити в чергу), а операцію видалення елемента — Dequeue (вивести з черги).

Подібно стековій операції Pop, операція Dequeue не потребує передачі елемента масиву, який необхідно видалити, у вигляді аргументу. Він визначений однозначно.

Завдяки властивості FIFO черга схожа, наприклад, на живу чергу до лікаря в поліклініці.

У неї є голова (head) і хвіст (tail). Коли елемент ставиться в чергу, він займає місце в її хвості, точно так само, як людина займає чергу останньою, щоб потрапити на прийом до лікаря. З черги завжди виводиться елемент, який знаходиться в її головній частині аналогічно тому, як в кабінет лікаря завжди заходить хворий, який чекав довше всіх.

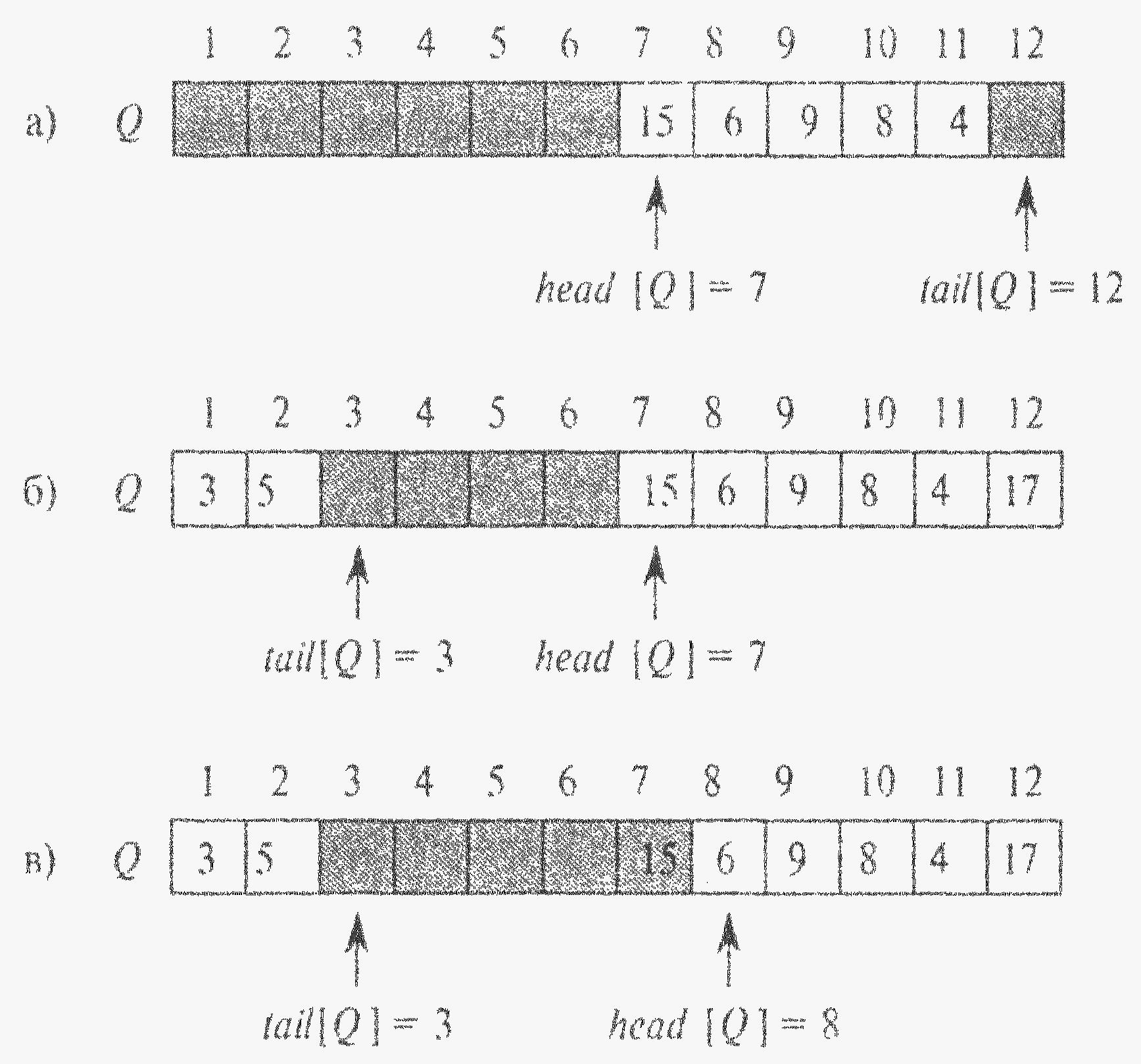
На малюнку черга реалізована за допомогою масиву Q [1..12].

Покажемо, як за допомогою масиву Q [1..n] можна реалізувати чергу, що складається не більше ніж з n-1 елементів.

head [Q] - індекс головного елемента або вказівник на нього;

tail [Q] – індексує місцезнаходження, куди буде добавлено новий елемент.

Елементи черги знаходяться у клітинках

head [Q], head [Q] +1,..., tail [Q] -1, які циклічно замкнені (клітинка 1 слідує відразу ж після клітинки n в циклічному порядку).

На мал. елементи черги знаходяться лише у світлих клітинках.

На мал. а) зображена черга, яка складається з п’яти елементів, що знаходяться у клітинках Q [7.. 11]. Мал. б) - це та ж черга після виклику процедур Enqueue(Q, 17), Enqueue(Q,3) та Enqueue(Q, 5).

Мал. в) - черга після виклику Dequeue(Q), що повертає значення ключа 15, яке до цього знаходилось у голові черги.

Значення ключа нової голови черги дорівнює 6. Кожна операція виконується протягом часу О(1).

При виконанні умови head [Q] = tail [Q] черга порожня

(т.к. за доп. масиву Q [1..n] можна реалізувати чергу, що складається не більше ніж з n-1 елементів).

З самого початку виконується співвідношення head [Q] = tail [Q]= 1.

Якщо черга порожня, то при спробі видалити з неї елемент відбувається помилка спустошення.

Якщо head [Q] = tail [Q]+1, то черга заповнена, і спроба додати до неї елемент призводить до її переповнення (один елем. масиву лишається не заповненим).

В наведених нижче процедурах Enqueue та Dequeue перевірка помилок спустошення та переповнення не виконується.

Enqueue(Q,x)

1 Q[tail[Q]]<-x

2 if tail[Q]=length[Q]

3 then tail[Q]<-1

4 else tail[Q]<-tail[Q]+1

Dequeue(Q)

1 x<-Q[head[Q]]

2 if head[Q]=length[Q]

3 then head[Q]<-1

4 else head[Q]<-head[Q]+1

5 return x

Математичні основи аналізу алгоритмів. Графи.

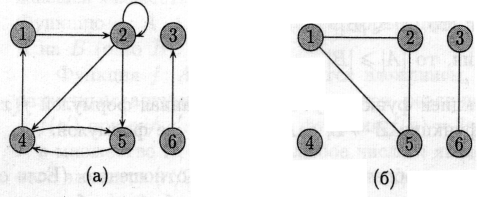
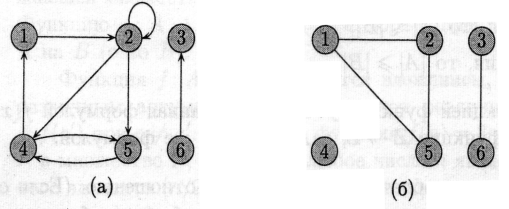
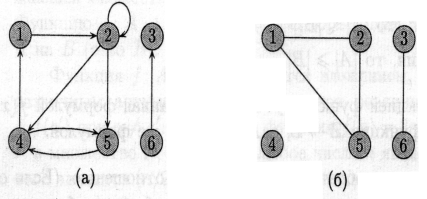
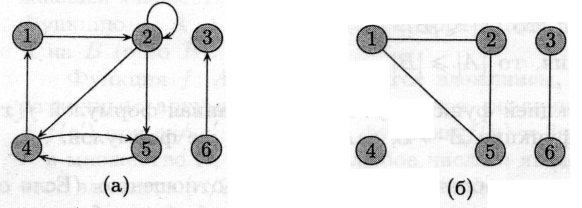
Орієнтований граф (directed graph) визначається як пара (V,E), де V — скінченна множина, а Е — бінарне відношення на V, тобто підмножина множини V х V. Орієнтований граф іноді для скорочення називають орграфом (digraph). Множину V називають множиною вершин графа (vertex set); її елемент називають вершиною графа (vertex, vertices). Множину Е називають множиною ребер (edge set) графа; її елементи називають ребрами (edges).

На малюнку (а) показаний орієнтований граф с множиною вершин {1, 2, 3, 4, 5, 6}. Вершини зображені кружками, а ребра — стрілками. Граф може мати ребра-цикли (self-loops), що з’єднують вершину з собою.

О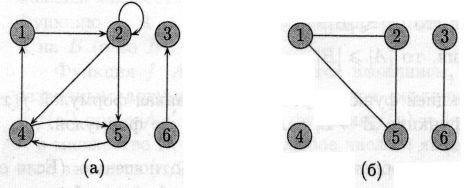 рієнтований граф, що не має ребер-циклів, називається простим (simple).

Про ребро (u,v) орієнтованого графа говорять, що воно виходить з

вершини и і входить у вершину v. Наприклад, маємо три ребра, що

виходять із вершини 2 ((2, 2), (2, 4), (2, 5)) і два ребра, що в неї

входять ((1,2), (2,2)).

В неорієнтованому (undirected) графі G = (V, Е) множина ребер Е складається з невпорядкованих (unordered) пар вершин: парами є множини {u,v}, де и, v Î V і и ≠ v. Для неорієнтованого графа (и, v) і (v, и) позначають одне і те ж ребро. Неорієнтований граф не може містити ребер-циклів, і кожне ребро складається з двох різних вершин («з’єднуючи» їх). На мал. (б) зображено неорієнтований граф с множиною вершин {1,2,3,4,5,6}.

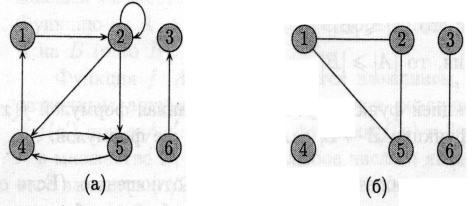
Про ребро (и, v) неорієнтованого графа говорять, що воно інцидентне вершинам и та v. Наприклад, на мал. (б) є два ребра, інцидентні Вершині 2 (ребра (1,2) та (2,5)).

Якщо в графі G є ребро (и, v), говорять, що вершина v суміжна з вершиною и.

Для неорієнтованих графів відношення суміжності є симетричним.

Для орієнтованих графів це не обов’язково. Якщо вершина v суміжна з вершиною и в орієнтованому графі, пишуть и —> v.

Для обох малюнків (а) та (б) вершина 2 є суміжною з вершиною 1, але лише на другому з них вершина 1 суміжна с вершиною 2 (в першому випадку ребро (2,1) відсутнє в графі).

Степенем (degree) вершини в неорієнтованому графі називається кількість інцидентних їй ребер. Наприклад, для графу на мал. (б) степінь вершини 2 дорівнює 2.

Для орієнтованого графа розрізняють вихідний степінь (out-degree), що визначається як кількість ребер, які з неї виходять, і вхідний степінь (in-degree), що визначається як кількість ребер, які в неї входять. Сума вихідного та вхідного степенів називається степінем (degree) вершини. Наприклад, вершина 2 в графі мал. (а) має вхідний степінь 2, вихідний степінь 3 та степінь 5.

Шлях довжини к з вершини и в вершину v визначається як послідовність вершин (v₀, v₁, v₂, ... , v_k), в якій v₀ = и, v_k = v і (v_i-1, v_i) Î Е для всіх i = 1, 2,..., к.

Таким чином, шлях довжини к складається з к ребер. Цей шлях містить вершини v₀, v₁, v₂, ... , v_k і ребра (v₀, v₁), (v₁, v₂), …, (v_k-1, v_k).

Шлях називається простим, якщо всі вершини в ньому різні. Наприклад, на мал. (а) є простий шлях (1,2,5,4) довжини 3, а також шлях (2,5,4,5) такої ж довжини, що не є простим.

Циклом в орієнтованому графі називається шлях, в якому початкова вершина співпадає з кінцевою і який містить хоча б одне ребро.

Цикл (v₀, v₁, v₂, ... , v_k) називається простим, якщо в ньому немає однакових вершин (окрім першої та останньої), тобто якщо всі вершини v₁, v₂, ... , v_k різні. Ребро-цикл є циклом довжини 1.

Будемо ототожнювати цикли, які відрізняються здвигом вздовж циклу: один і той же цикл довжини к може бути представлений к різними шляхами (в якості початку і кінця можна взяти будь-яку з к вершин). Наприклад, на мал. (а) шляхи (1, 2, 4, 1), (2, 4, 1, 2) і (4, 1, 2, 4) є одним і тим же циклом. Цей цикл є простим, тоді як цикл (1,2,4,5,4,1) таким не є. На тому ж малюнку є цикл (2,2), утворений єдиним ребром-циклом (2,2).

В неорієнтованому графі шлях (v₀, v₁, v₂, ... , v_k), називається (простим) циклом, якщо к ≥ 3, v₀ = v_k і всі вершини v₁, v₂, ..., v_k різні. Наприклад, на мал. (б) є простий цикл (1, 2, 5,1).

Граф, в якому немає циклів, називається ациклічним (acyclic).

Неорієнтований граф називається зв’язним, якщо для будь-якої пари вершин існує шлях з однієї в іншу.

Деякі види графів мають спеціальні назви.

Повним (complete) графом називають неорієнтований граф, що містить всі можливі ребра для даної множини вершин (будь-яка вершина суміжна з будь-якою іншою).

Неорієнтований граф (V, Е) називають дводольний (bipartite), якщо множину вершин V можна розбити на дві частини V1 і V2 таким чином, що кінці будь-якого ребра виявляються в різних частинах.

Ациклічний неорієнтований граф називають лісом (forest).

Зв’язний ациклічний неорієнтований граф називають деревом без виділеного кореня.

Дерева без виділеного кореня

Зв’язним ациклічний неорієнтований граф називають деревом без виділеного кореня.

Якщо неорієнтований граф є ациклічним, але незв’язним, його називають лісом (forest); ліс складається з дерев ( що є його зв’язними компонентами).

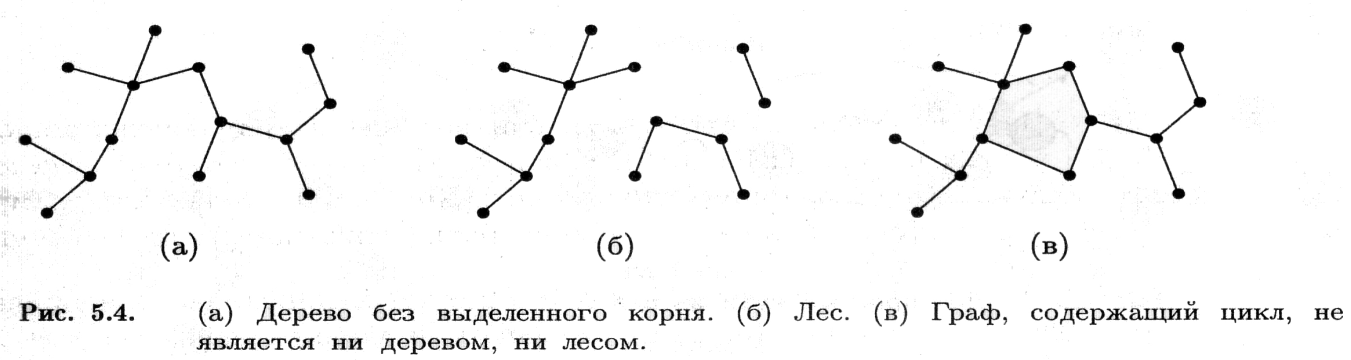
Дерева з коренем

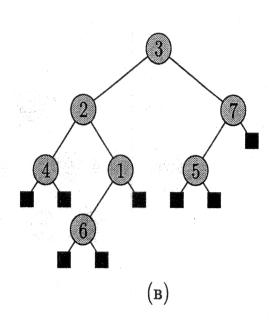
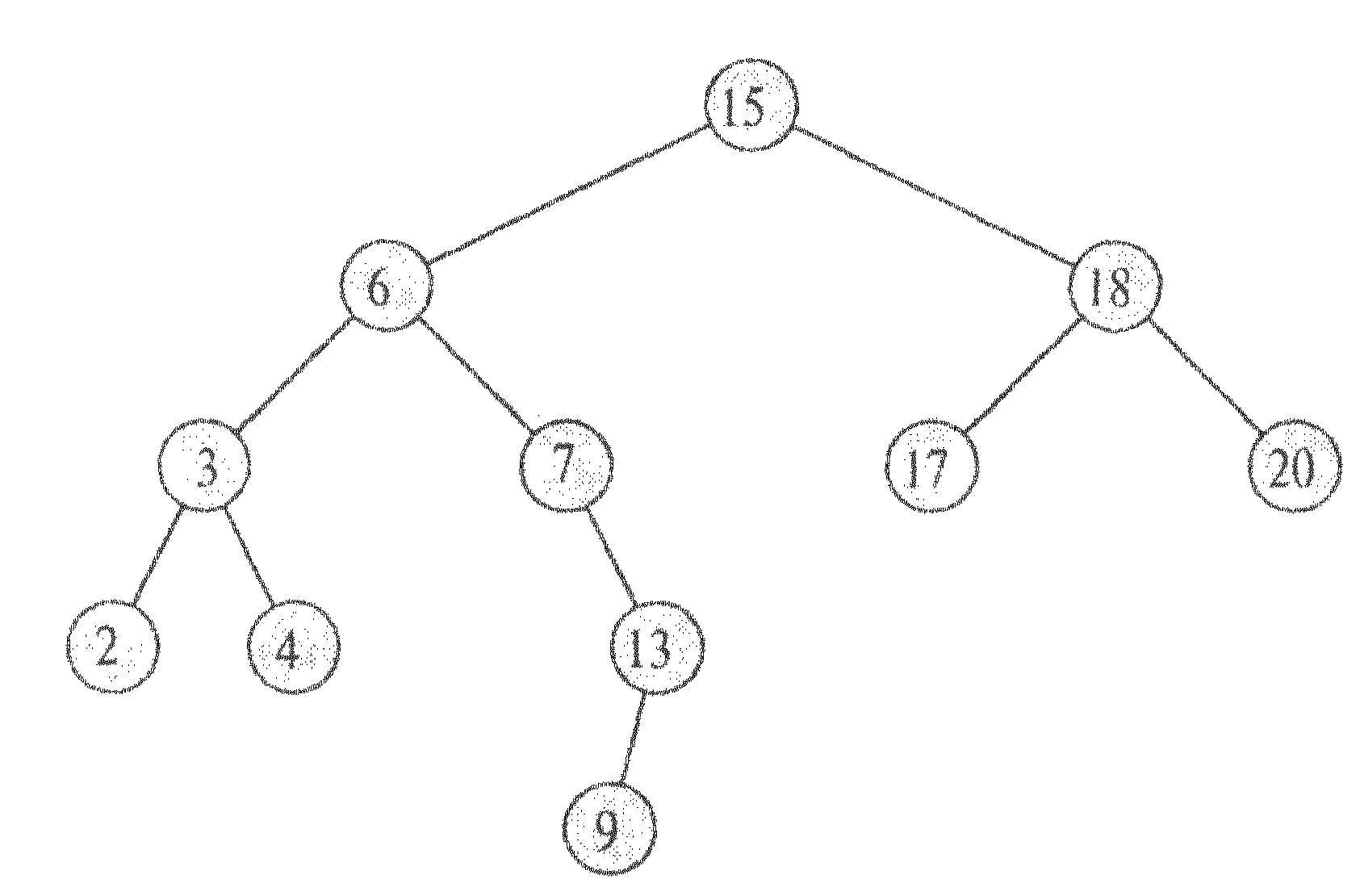
Дерево с коренем , або кореневе дерево (rooted tree), отримується, якщо в дереві (зв’язному ациклічному неорієнтованому графі) виділити одну із вершин, назвавши її коренем (root). На малюнку (а) показано кореневе дерево з 12 вершинами і коренем 7.

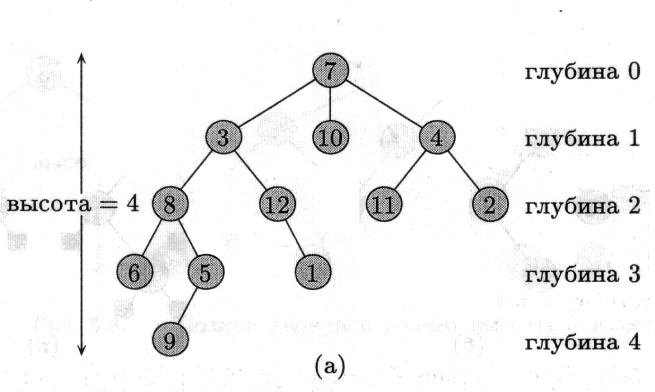
Дерева з коренем

Нехай x — будь-яка вершина кореневого дерева з коренем r. Існує єдиний шлях із r в x; всі вершини, що знаходяться на цьому шляху, називаються предками вершини x. Якщо у є предком x, то x називається потомком у.

Якщо (у, x) — останнє ребро на шляху з кореня в x, то у називається батьком x, а x називається дитиною у. Корінь є єдиною вершиною, у якої немає батька.

Вершини, що мають спільного батька, будемо називати братами.

Вершина кореневого дерева, яка не має дітей, називається листком.

Вершини, що мають дітей, називаються внутрішніми (internal).

Кількість дітей у вершини кореневого дерева називається її степенем.

Для всіх вершин, окрім кореня, степінь на одиницю менше степеня тієї ж вершини в тому ж дереві, якщо розглядати дерево як неорієнтований граф (оскільки тоді потрібно враховувати і ребро, що йде вверх).

Довжина шляху від кореня до будь-якої вершини x називається глибиною вершини x. Максимальна глибина вершин дерева називається висотою дерева.

Деревом с порядком на дітях називається кореневе дерево з додатковою структурою: для кожної вершини множина її дітей впорядкована (відомо, який її нащадок перший, який другий і т.д.). Два дерева на мал. однакові як кореневі дерева, але різні як дерева з порядком на дітях.

Двійкові дерева. Позиційні дерева

Двійкове дерево (binary tree) можна визначити рекурсивно як скінченний набір вершин, який:

• або пустий (не містить вершин),

• або розбитий на три частини, які не перетинаються: вершину, що називається коренем (root), двійкове дерево, що називається лівим піддеревом (left subtree) кореня, і двійкове дерево, що називається правим піддеревом (right subtree) кореня.

Двійкове дерево, що не містить вершин, називається пустим (empty). Воно позначається NIL.

Порожні місця в двійковому дереві часто заповнюють фіктивними листками. Після цього у кожної старої вершини буде двоє дітей (або колишніх, або доданих).

Можна визначити аналоги двійкових дерев для дерев більшого степеня: двійкові дерева (бінарні) є окремим випадком k-арних дерев при k = 2.

Позиційне дерево визначається як кореневе дерево, в якому діти будь-якої вершини помічені різними цілими додатними числами, які є їх номерами. При цьому у кожної вершини є вакансії для дітей номер 1, 2, 3 і так далі, з яких деякі (скінченна кількість) заповнені, а інші вільні.

При цьому k-арним деревом називається позиційне дерево, що не має вершин з номерами більшими за k.

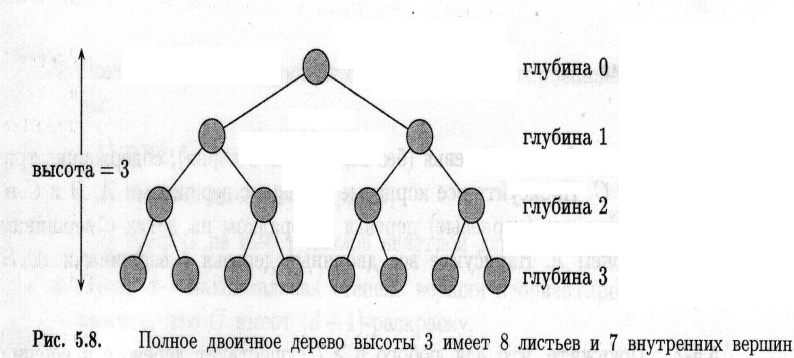
Повним k-арним деревом називається k-арне дерево, в якому всі листки мають однакову глибину и всі внутрішні вершини мають степінь k. Структура такого дерева повністю визначається його висотою. На мал. показано повне двійкове дерево висотою 3.

П ідрахуємо, скільки листків має повне k-арне дерево висотою h. Корінь є єдиною вершиною глибини 0, його k дітей є вершинами глибини 1, їх дітьми є k² вершин глибини 2 і так далі аж до k^h листків глибини h. Висота k-арного дерева з n листками дорівнює log_kn (таке дерево існує, тільки якщо цей логарифм цілий). Кількість внутрішніх вершин повного k-арного дерева висоти h дорівнює (сума чл. геом. прогрес.)

Зокрема, для повного двійкового дерева кількість внутрішніх вершин на одиницю менша кількості листків.

Представлення бінарного (двійкового) дерева Т. Кожна вершина х включає поля р[х] (зверху) - вказівник на батьківський вузол, left[x] (внизу зліва) - вказівник на дочірній лівий вузол, right[x] (внизу справа) - вказівник на дочірній правий вузол. Ключі на схемі не показані.

Якщо р [х] = nil, то х — корінь дерева.

Якщо у вузла х немає дочірніх вузлів, то

left [х] = right [х] = nil.

Атрибут root [T] вказує на кореневий вузол дерева T.

Якщо root [T] = NIL, то дерево Т пусте.

Представлення кореневих дерев. Двійкові дерева пошуку

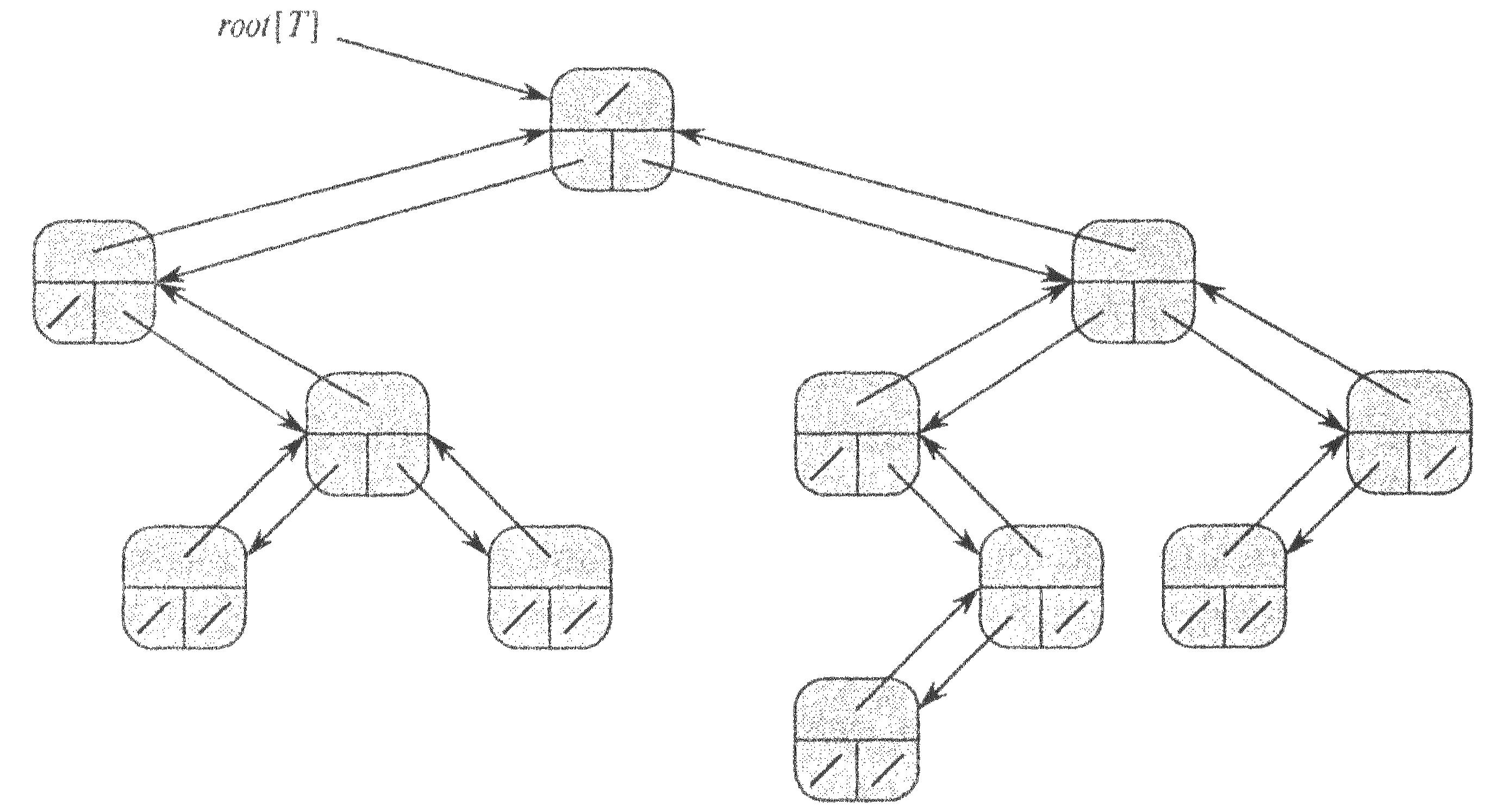
Представлення бінарного (двійкового) дерева Т. Кожна вершина х включає поля р[х] (зверху) - вказівник на батьківський вузол, left[x] (внизу зліва) - вказівник на дочірній лівий вузол, right[x] (внизу справа) - вказівник на дочірній правий вузол. Ключі на схемі не показані.

Якщо р [х] = nil, то х — корінь дерева.

Якщо у вузла х немає дочірніх вузлів, то

left [х] = right [х] = nil.

Атрибут root [T] вказує на кореневий вузол дерева T.

Якщо root [T] = NIL, то дерево Т пусте.

Схему представлення бінарних дерев можна узагальнити для дерев будь-якого класу, в яких кількість дочірніх вузлів не перевищує деякої константи k. При цьому поля правий і лівий замінюється полями child₁, child₂ ..., child_k.

Якщо кількість дочірніх елементів вузла не обмежена, то ця схема не працює, оскільки заздалегідь не відомо, місце для якої кількості полів потрібно виділити. Крім того, якщо кількість дочірніх елементів k обмежено великою константою, але насправді у багатьох вузлів нащадків набагато менше, то значний об'єм пам'яті витрачається марно.

Будь-яке дерево можна перетворити в двійкове. При цьому в кожної вершини буде не більше двох дітей: ліве дитя залишиться тим же, а правим дитям стане вершина, яка була правим сусідом (безпосередньо наступним дитям того ж батька).

Схема зберігання дерев з довільним розгалуженням, основана на цій ідеї, називається «Ліве дитя — правий сусід» (left-child, right-sibling representation) або представлення з лівим дочірнім і правим сестринським вузлами.

Як і раніше в кожній вершині зберігається вказівник р на батька і атрибут root[T] є вказівником на корінь дерева. Окрім р, в кожній вершині зберігаються ще два вказівники:

1. left-child[x] вказує на найлівіше дитя вершини х;

2. right-sibling[x] вказує на найближчого справа сусіда вершини х («наступного за старшинством брата»)

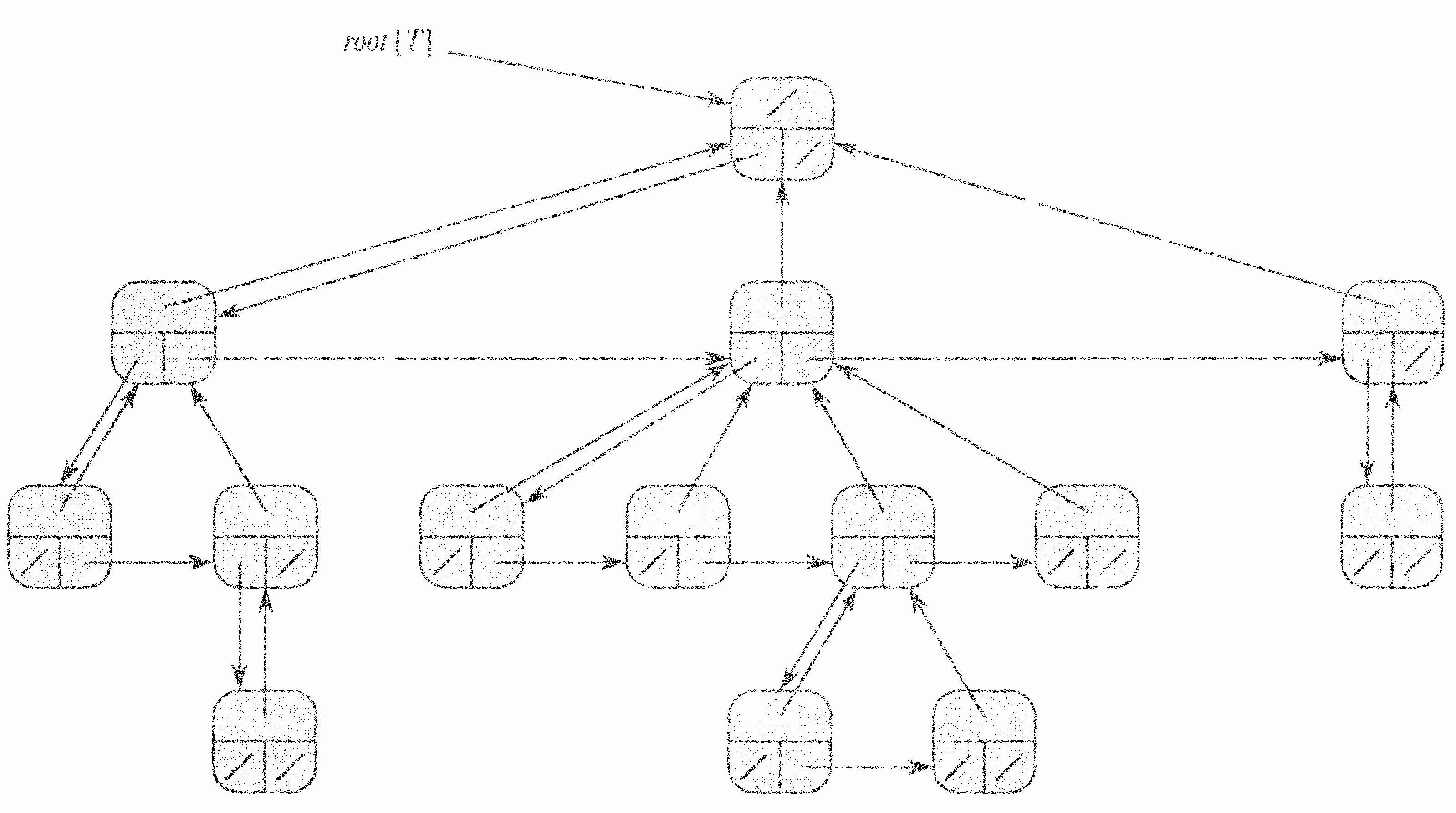
Якщо вузол х не має нащадків, то

left - child [x] = NIL ,

а якщо вузол х - крайній правий дочірній елемент якогось батьківського елементу, то right - sibling [x] = NIL.

У двійковому дереві пошуку (binary search tree) кожна вершина може мати (або не мати) ліву і праву дитину; кожна вершина, окрім кореня, має батька. При представленні з використанням вказівників ми зберігаємо для кожної вершини дерева, окрім значення ключа key і додаткових даних, також і вказівники left, right і р (ліве дитя, праве дитя, батько). Якщо дитини (або батька — для кореня) немає, відповідне поле містить NIL.

Ключі в двійковому дереві пошуку зберігаються з дотриманням властивості впорядкованості (binary-search-tree property):

• Нехай х - довільна вершина двійкового дерева пошуку. Якщо вершина y знаходиться в лівому піддереві вершини х, то key[y] <= key[x]. Якщо y знаходиться в правому піддереві х, то кеу[у] >= кеу[х].

• Властивість впорядкованості дозволяє надрукувати всі ключі в неспадаючому порядку за допомогою простого рекурсивного алгоритму (inorder tree walk). Цей алгоритм друкує ключ кореня піддерева після всіх ключів його лівого піддерева, але перед ключами правого піддерева (центрований (симетричний) обхід дерева).

• Порядок, при якому корінь передує обом піддеревам, називається preorder (обхід в прямому порядку); порядок, в якому корінь слідує за ними, називається postorder (обхід в зворотному порядку).

Дерева пошуку (search trees) дозволяють виконувати наступні операції з динамічними множинами: Search (пошук), Minimum (мінімум), Maximum (максимум), Predecessor (попередній), Successor (наступний), Insert (вставити) і Delete (видалити). Основні операції в бінарному дереві пошуку виконуються за час, пропорційний його висоті (час виконання Θ(log n)).

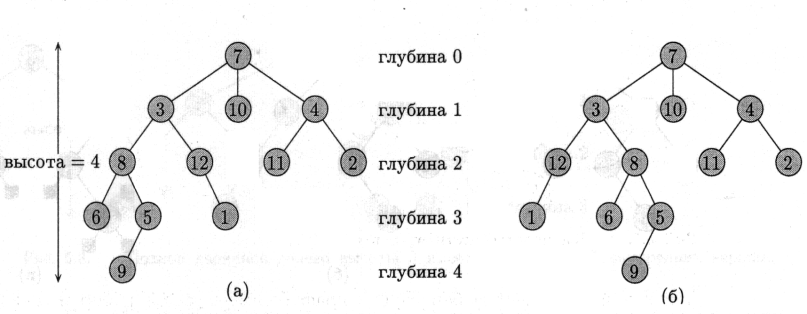
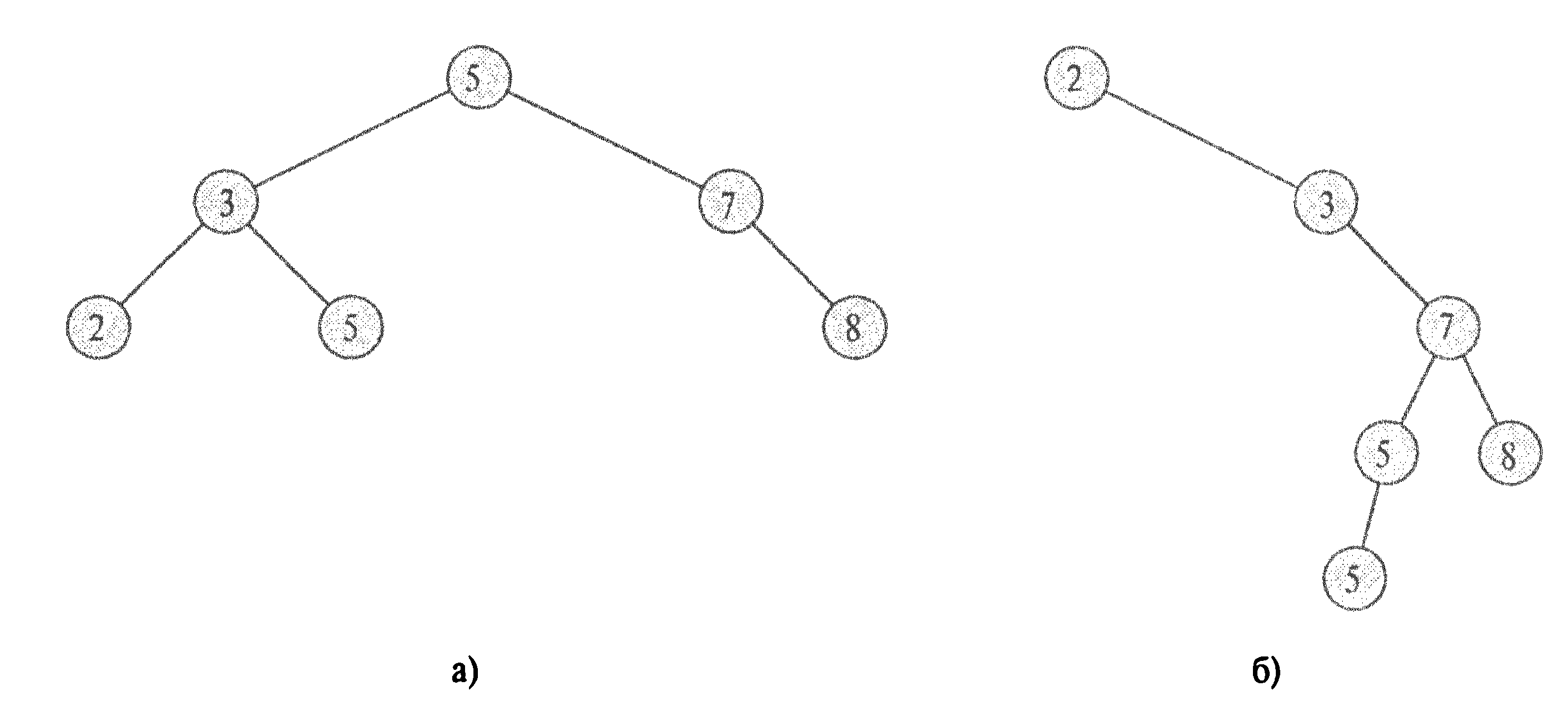
Різні двійкові дерева пошуку можуть представляти одну і ту ж множину. (а) Двійкове дерево пошуку висоти 2 з 6 вершинами. (б) Менш ефективне дерево висоти 4, що містить ті ж ключі.

Виклик Inorder-Tree-Walk (root[Т]) друкує (використовуючи центрований обхід) всі ключі, що входять в дерево T з коренем root[T].

Наприклад, для обох дерев мал. (а) і (б) буде надруковано 2,3,5,5,7,8.

Час роботи цієї процедури на дереві з n вершинами є Θ(n): на кожну вершину витрачається обмежений час (окрім рекурсивних викликів) і кожна вершина обробляється один раз.

Найбільш поширеною операцією, що виконується з бінарним деревом пошуку, є пошук в ньому певного ключа. Розглянемо операції пошуку, знаходження мінімального та максимального, попереднього та наступного елементу і покажемо, що всі вони можуть бути виконані в бінарному дереві пошуку висотою h за час О(h).

Процедура пошуку отримує на вхід шуканий ключ k і вказівник х на корінь піддерева, в якому проводиться пошук. Вона повертає вказівник на вершину з ключем k (якщо така є) або спеціальне значення NIL (NULL) (якщо такої вершини немає).

В процесі пошуку ми рухаємося від кореня, порівнюючи ключ k з ключем, що зберігається в поточній вершині х. Якщо вони рівні, пошук завершується.

Якщо k<кеу[х], то пошук продовжується в лівому піддереві х (ключ k може бути лише там, згідно властивості впорядкованості).

Якщо k>кеу[х], то пошук продовжується в правому піддереві.

Наприклад, для пошуку ключа 13 ми повинні пройти наступний шлях від кореня: 15 -> 6 -> 7 -> 13. Вузли, які ми відвідуємо при рекурсивному пошуку, утворюють низхідний шлях від кореня дерева, так що час роботи процедури пошуку рівний O(h): (де h - висота дерева).

Ось ітераційна версія тієї ж процедури (яка, як правило, ефективніша):

Мінімальний ключ в дереві пошуку можна знайти, пройшовши за вказівниками left від кореня (поки не впремося в nil). Процедура повертає вказівник на мінімальний елемент піддерева з коренем х .

Властивість впорядкованості гарантує правильність процедури Tree-Minimum.

Якщо у вершини x немає лівої дитини, то мінімальний елемент піддерева з коренем x є x, оскільки будь-який ключ в правому піддереві не менший кеу[х].

Якщо ж ліве піддерево вершини x не порожнє, то мінімальний елемент піддерева з коренем x знаходиться в цьому лівому піддереві (оскільки сам x і всі елементи правого піддерева більші).

Алгоритм Tree-Maximum симетричний.

Обидва алгоритми вимагають часу O(h), де h - висота дерева (оскільки рухаються по дереву лише вниз).

Інколи, маючи вузол в бінарному дереві пошуку, потрібно визначити, який вузол слідує за ним у відсортованій послідовності, що визначається порядком центрованого обходу бінарного дерева, і який вузол передує даному.

Якщо всі ключі різні, наступний по відношенню до вузла х є вузол з найменшим ключем, більшим за key [x].

Структура бінарного дерева пошуку дозволяє нам знайти цей вузол навіть не виконуючи порівняння ключів. Приведена далі процедура повертає вузол, наступний за вузлом х в бінарному дереві пошуку (якщо такий існує) і NIL, якщо х має найбільший ключ в бінарному дереві (останній в дереві).

Процедура Tree-successor окремо розглядає два випадки. Якщо праве піддерево вершини х не порожнє, то наступний за х елемент — це мінімальний елемент в цьому піддереві і рівний Tree-Minimum(right[x]).

Нехай тепер праве піддерево вершини х порожнє. Тоді ми йдемо від х вгору, поки не знайдемо вершину, що є лівим сином свого батька (рядки 3-7). Цей батько (якщо він є) і буде шуканим елементом.

Час роботи процедури Tree-Successor на дереві висоти h є O(h), оскільки ми рухаємося або лише вгору, або лише вниз.

Процедура Tree-Predecessor симетрична.

Таким чином, операції Search, Minimum, Maximum, Successor і Predecessor на дереві висоти h виконуються за час О(h).

Ці операції змінюють дерево, зберігаючи властивість впорядкованості.

Додавання елементу

Процедура Tree-Insert додає заданий елемент у відповідне місце дерева T (зберігаючи властивість впорядкованості). Параметром процедури є вказівник z на нову вершину, в яку поміщені значення key[z] (значення ключа, що додається), left[z]= NIL і right[z]= NIL.

В ході роботи процедура змінює дерево T і (можливо) деякі поля вершини z, після чого нова вершина з даним значенням ключа виявляється вставленою у відповідне місце дерева.

Рухаємося вниз по дереву, почавши з його кореня. При цьому у вершині y зберігається вказівник на батька вершини х (цикл в ряд. 3-7). Порівнюючи key[z] з кеу[х], процедура вирішує, куди йти — наліво чи направо. Процес завершується, коли х стає рівним NIL. NIL стоїть якраз там, куди треба помістити z, що і робиться у ряд. 8-13.

Видалення елементу

Параметром процедури видалення є вказівник на вершину, що видаляється. При видаленні можливі три випадки.

1. Якщо у z немає дітей, для видалення z досить помістити NIL у відповідне поле його батька (замість z).

2. Якщо у z є одне дитя, можна «вирізати» z, з'єднавши його батька безпосередньо з його дитям.

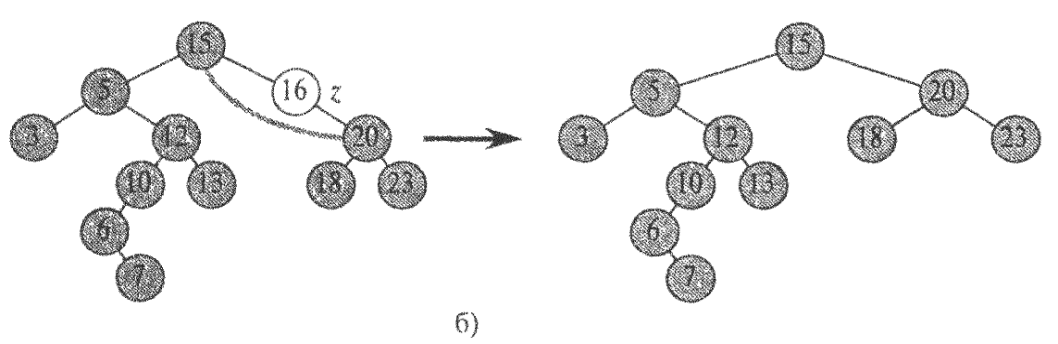
3. Якщо ж дітей двоє, потрібні деякі приготування: ми знаходимо наступний (у сенсі порядку на ключах) за z елемент у; у нього немає лівої дитини. Тепер можна скопіювати ключ і додаткові дані з вершини у у вершину z, а саму вершину у видалити описаним вище способом.

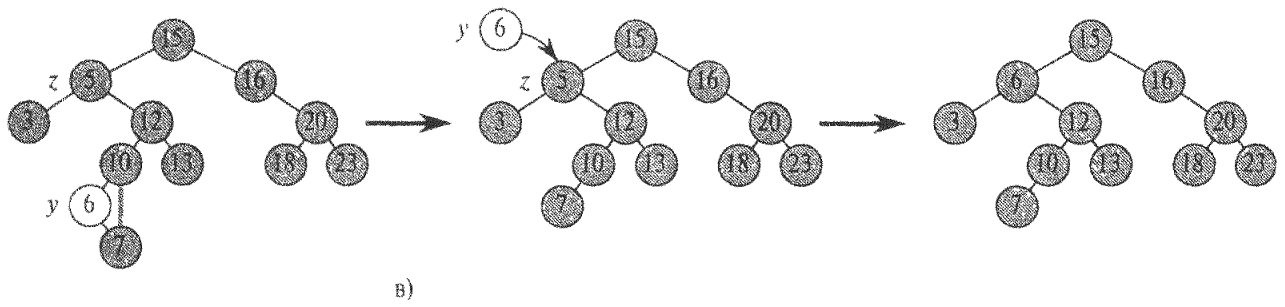
У ряд. 1-3 визн. вершина у, яку потім виріжемо з дерева. Це або сама вершина z (якщо у z не більше однієї дитини), або наступний за z елемент (якщо у z двоє дітей).

У ряд. 4-6 змінна x стає вказівником на існуючу дитину вершини у, або рівною NIL, якщо у у немає дітей.

У рядках 7-13 вершина у вирізається з дерева (міняються вказівники в вершинах р[у] і x). Окремо розглядаються граничні випадки, коли x = NIL і коли у є коренем дерева.

У рядках 14-16, якщо вирізана вершина у відмінна від z, ключ (і додаткові дані) вершини у переміщаються в z (адже нам треба було видалити z, а не у). Нарешті, процедура повертає вказівник у (це дозволить викликаючій процедурі згодом звільнити пам'ять, зайняту вершиною у).

Таким чином, операції Insert і Delete можуть бути виконані за час O(h), де h — висота дерева.

Хеш-таблиці

Для багатьох додатків достатньо використовувати динамічні множини, які підтримують лише стандартні словникові операції вставки, пошуку та видалення.

Хеш-таблиця є ефективною структурою даних для реалізації словників. Хоча на пошук елемента в хеш-таблиці може в найгіршому випадку знадобитися стільки ж часу, як і у зв’язаному списку, а саме O(n), на практиці хешування дуже ефективне. При досить обґрунтованих припущеннях математичне очікування часу пошуку елемента в хеш-таблиці складає O(1).

Пряма адресація є елементарною технологію, що добре працює для невеликих множин ключів. Нехай додаток потребує динамічну множину, кожний елемент якої має ключ із множини U={0,1,..., m-1}, де m не дуже велике. Крім того, вважатимемо, що ніякі два елементи не мають однакових ключів.

Для представлення динамічних множин ми використовуємо масив, або таблицю з прямою адресацією, котрий позначимо як Т [0..m-1], кожна позиція, чи комірка, якого відповідає ключу із простору ключів U.

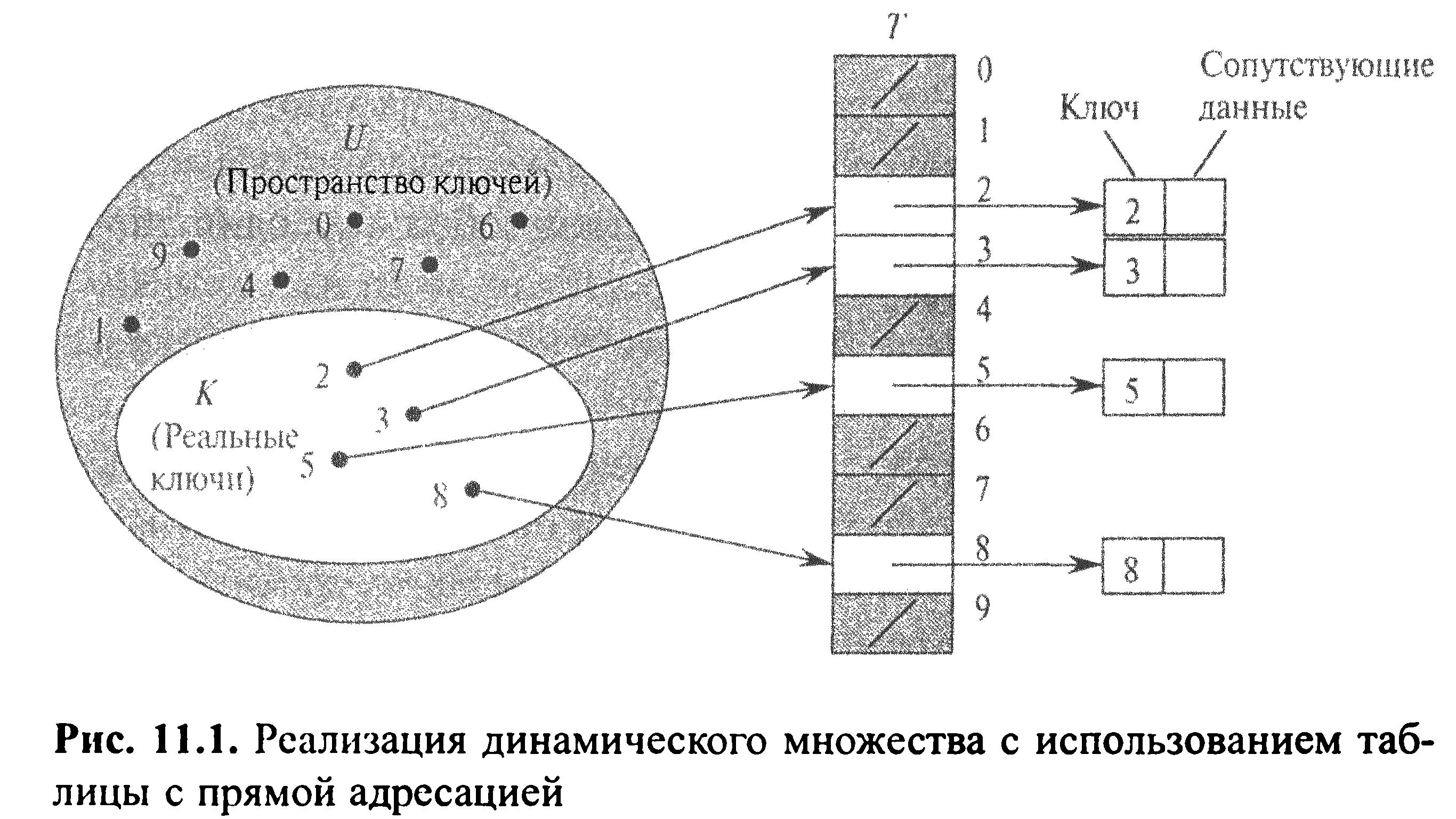
На рис. комірка к вказує на елемент множини з ключем к. Якщо множина не містить елемента з ключем к, то Т [к] = NIL. На рис. кожний ключ із простору U = {0,1,..., 9} відповідає індексу таблиці. Множина реальних ключів К = {2,3,5,8} визначає комірки таблиці, які містять вказівники на елементи. Інші комірки(зафарбовані темним кольором) містять значення nil.

Реалізація словарних операцій тривіальна:

Кожна з наведених операцій дуже швидка: час їх роботи рівний О(1).

Недолік прямої адресації: якщо простір ключів U великий, зберігати таблицю Т розміром |U| непрактично, або взагалі неможливо — в залежності від кількості доступної пам’яті та розміру простору ключів. Крім того, множина К реально збережених ключів може бути малою в порівнянні з простором ключів U, в цьому випадку пам’ять, що виділена для таблиці Т, в основному витрачається даремно.

Коли множина К, ключів, що зберігаються у словнику, набагато менша простору можливих ключів U, хеш-таблиця потребує істотно менше місця, ніж таблиця з прямою адресацією (вимоги до пам’яті можуть бути знижені до Θ(|К|) ).

У випадку прямої адресації елемент із ключем к зберігається в комірці к. При хешуванні цей елемент зберігається в комірці h(к), тобто ми використовуємо хеш-функцію h для розрахунку комірки для даного ключа к. Функція h відображає простір ключів U на комірки хеш-таблиці Т [0..m-1]:

h: U -> {0,1,...,m-1}.

Елемент з ключем к хешується в комірку h(к); величина h(к) називається хеш-значенням ключа к. Ціль хеш-функції: зменшити робочий діапазон індексів масиву, і замість |U| значень ми можемо обійтися всього лиш m значеннями . Відповідно знижуються і вимоги до кількості пам’яті.

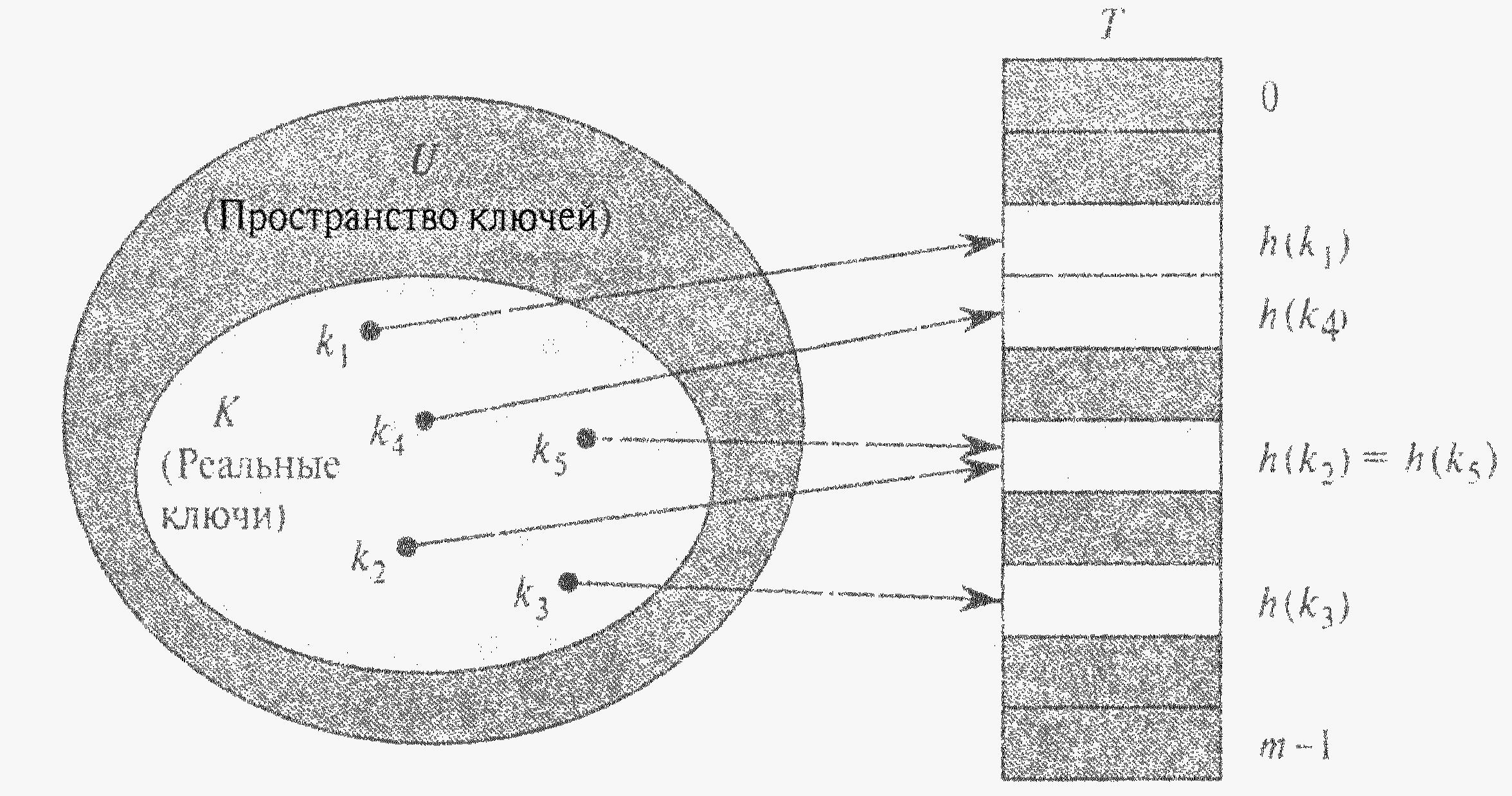
Однак хеш-значення двох різних ключів можуть збігатися. В таких випадках кажуть, що трапилась колізія, або зіткнення (collision). На рис. ключі k₂ та k₅ відображаються в одну комірку, викликаючи колізію. Існують ефективні технології для вирішення конфліктів, що виникають через колізію.

Найпростіший метод обробки (вирішення) колізій — метод ланцюжків. Інший спосіб — метод відкритої адресації.

При використанні даного методу ми об'єднуємо всі елементи, хешовані в одну й ту ж комірку, у зв’язний список. Комірка j містить вказівник на заголовок списку всіх елементів, хеш-значення ключа яких дорівнює j; якщо таких елементів немає, комірка містить значення NIL.

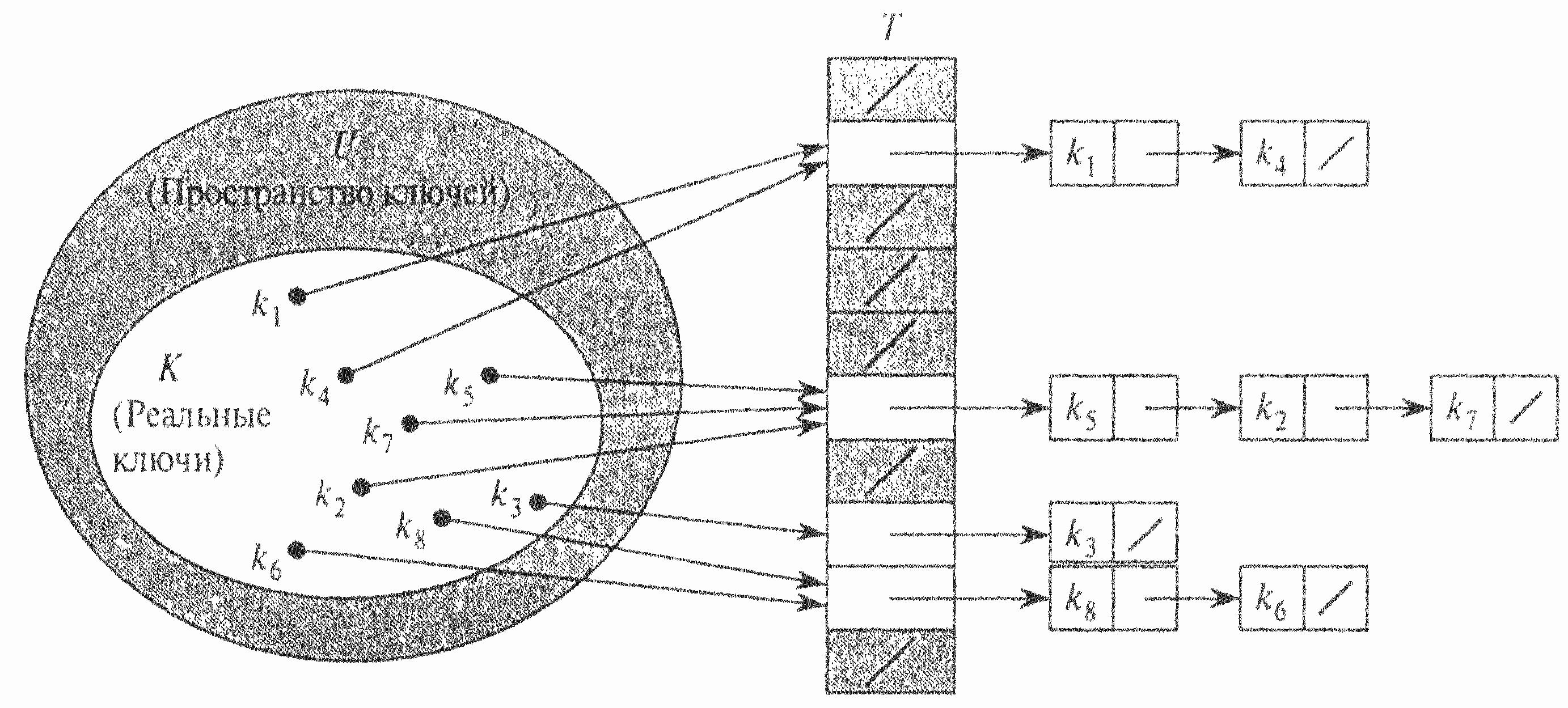
Показано вирішення колізій, які виникають через те, що h(k1)=h(k4), h(k5)=h(k2)=h(k7) та h(k8)=h(k6).

Словникові операції в хеш-таблиці з використанням ланцюжків для вирішення колізій реалізуються дуже просто:

Час, потрібний для вставки, в найгіршому випадку, рівний O(1) (елемент х вставляється в голову списку Т[h(key[x])] ).

Час роботи пошуку, в найгіршому випадку, пропорційний довжині списку.

Видалення елемента може бути виконано за час O(1) при використанні двозв’язних списків (оскільки процедура Chained_Hash_Delete приймає в якості аргументу елемент х (вказівник), а не його ключ, тому немає необхідності в попередньому пошуку х. Якщо список однозв’язний, тоді передача в якості аргументу х не дає нам особливого виграшу, оскільки для коректного оновлення поля next елемента, що стоїть перед х, нам все одно потрібно виконати пошук х в списку Т[h(key[x])]. В такому випадку видалення та пошук мають по суті один й той самий час роботи.)

Якісна хеш-функція задовольняє (наближено) припущенню простого рівномірного хешування: для кожного ключа рівноймовірним є розміщення в будь-якій з m комірок, незалежно від хешування інших ключів.

Побудова хеш-функції методом ділення полягає у відображенні ключа к в одну з комірок шляхом отримання остачі від ділення к на m, тобто хеш-функція має вигляд

h(k) = к mod m.

Наприклад, якщо хеш-таблиця має розмір m = 12, а значення ключа к = 100, то h (к) = 4. Оскільки для обчислення хеш-функції потрібна тільки одна операція ділення, хешування методом ділення є достатньо швидким.

Часто хороші результати можна отримати, вибираючи в якості значення m просте число, досить віддалене від степеня двійки.

Припустимо, наприклад, що нам потрібно помістити близько 2000 записів в хеш-таблицю ланцюжками, причому нас не лякає можливий перебір трьох варіантів при пошуку відсутнього в таблиці елемента. Використаємо метод ділення з остачею при довжині хеш-таблиці m = 701. Число 701 просте, 701 ≈ 2000/3, і не є степенем 2. Таким чином, можна вибрати хеш-функцію вигляду:

h(k) = k mod 701.

Побудова хеш-функції методом множення виконується у два етапи. Спочатку ми множимо ключ к на константу 0 < А < 1 і отримуємо дробову частину від отриманого добутку. Потім ми множимо отримане значення на m і застосовуємо до нього функцію знаходження цілої частини, тобто

де вираз “kА mod 1" означає отримання дробової частини від добутку kА, тобто величину

-ціла частина х (найбільше ціле число, менше чи рівне х)

Перевага методу множення полягає у тому, що якість хеш-функції мало залежить від вибору m. Зазвичай в якості m вибирають степінь двійки, оскільки у більшості комп’ютерів множення на таке m реалізується як зсув слова.

Хоча описаний метод працює з будь-якими значеннями константи А, деякі значення дають кращі результати в порівнянні з іншими. Оптимальний вибір залежить від характеристик хешованих даних. Кнут запропонував використовувати значення А, що дає хороші результати, таке:

1. //Сортировка вставками

2. void InsertMethod (int *mas,int n)

3. {

4. int temp;

5. int j;

6. for (int i=0;i<n;i++)

7. {

8. temp=mas[i];

9. j=i-1;

10. while ((j>=0)&&(mas[j]>temp))

11. {

12. mas[j+1]=mas[j];

13. j=j-1;

14. mas[j+1]=temp;

15. }

16. }

17. }

Бульбашкова:

1. template<class T>

2. void swap(T* x, int i, int j) {

3. T tmp;

4. tmp = x[i]; x[i] = x[j]; x[j] = tmp;

5. }

6.  

7. template<class T>

8. void BubbleSort3(T* x) {

9. int last = -1;

10. for (int i = 0; i < n; i++) {

11. int k = i;

12. if (last > 0 && last > i) {

13. k = last;

14. }

15. for (int j = n-1; j > k; j-- ) {

16. if (x[j-1] > x[j]) {

17. swap(x, j-1, j);

18. last = j;

19. }

20. }

21. if (last == k) break;

22. }

23. }

Разделя́й и вла́ствуй (англ. divide and conquer) в информатике — важная парадигма разработки алгоритмов, заключающаяся в рекурсивном разбиении решаемой задачи на две или более подзадачи того же типа, но меньшего размера, и комбинировании их решений для получения ответа к исходной задаче. Разбиения выполняются до тех пор, пока все подзадачи не окажутся элементарными.Типичный пример — алгоритм сортировки слиянием. Чтобы отсортировать массив чисел по возрастанию, он разбивается на две равные части, каждая сортируется, затем отсортированные части сливаются в одну. Эта процедура применяется к каждой из частей до тех пор, пока сортируемая часть массива содержит хотя бы два элемента (чтобы можно было её разбить на две части). Время работы этого алгоритма составляет Θ(nlogn) операций, тогда как более простые алгоритмы требуют Θ(n2) времени, где n — размер исходного массива.

Медотом выбора

1. template<class T>

2. void SelectSort(T* x) {

3. T t;

4. /* Главный цикл до n-1, а не n, т.к.

5. последний остающийся элемент -

6. максимальный */

7. for (int i = 0; i < n-1; i++) {

8. int k = i;

9. t = x[i];

10. for (int j = i; j < n; j++) {

11. if (x[j] < t) {

12. k = j;

13. t = x[j];

14. }

15. }

16. x[k] = x[i];

17. x[i] = t;

18. }

19. }

Лінійний пошук - алгоритм послідовного пошуку заданого значення довільної функції на деякому її відрізку. Пошук значення функції здійснюється простим порівнянням чергового розглянутого значення (як правило пошук відбувається зліва направо, тобто від менших значень аргументу до більших) і, якщо значення збігаються (з тією або іншою точністю), то пошук вважається завершеним. Якщо відрізок має довжину N, то середня кількість перевірок у разі успіху - N/2, у противному випадку – N.

Приклад.

int function LinearSearch (Array A, int L, int R, int Key);

Begin

for X = L to R do

if A [X] = Key then return X

return -1; // елемент не знайдено

end;

Двійковий пошук — алгоритм знаходження заданого значення у впорядкованому масиві, який полягає у порівнянні серединного елемента масиву з шуканим значенням, і повторенням алгоритму для тієї або іншої половини, залежно від результату порівняння Трудомісткість алгоритму 1 + log₂n, де n — кількість елементів у масиві.

Приклад:

BinarySearch(A[0..N-1], value, low, high)

{ if (high < low)

return -1 // не знайдено

mid = (low + high) / 2

if (A[mid] > value)

return BinarySearch(A, value, low, mid-1)

else if (A[mid] < value)

return BinarySearch(A, value, mid+1, high)

else return mid // знайдено }

Червоно-чорні дерева

Основні операції з двійковим деревом пошуку висотою h можуть бути виконані за час O(h). Дерева ефективні, якщо їх висота мала. В найгіршому ж випадку дерева не більш ефективні, ніж списки.

Червоно-чорні дерева – це двійкові дерева пошуку, вершини яких розподілені на червоні і чорні. При цьому повинні задовольнятися певні вимоги, які гарантують, що глибини будь-яких двох листків відрізняються не більше ніж вдвічі. Тому ці дерева можна назвати збалансованими. Спеціальні операції балансування гарантують, що висота дерева не перевищить O(logn).

Кожна вершина червоно-чорного дерева має поля: color (колір), key (ключ), left (ліва дитина), right (права дитина) і р (батько). Якщо вершина не має дитини чи батька, відповідне поле містить nil(NULL). Для зручності будемо вважати, що значення NULL, які зберігаються в полях left і right, є вказівниками на додаткові (фіктивні) листки дерева. В такому доповненому дереві кожна вершина, яка містить ключ і має двох дітей, стає внутрішньою вершиною.

Визначення

Двійкове дерево пошуку називається червоно-чорним деревом, якщо йому притаманні такі властивості (RB-властивості):

1. кожна вершина - або червона, або чорна;

2. корінь дерева є чорним;

3. кожний листок дерева (nil) - чорний;

4. якщо вершина червона, обидві її дитини чорні;

5. всі шляхи, які ведуть вниз від кореня до листків, містять однакову кількість чорних вершин.

Кількість чорних вершин на шляху від вершини х (не рахуючи саму вершину x ) до листка будемо називати чорною висотою вершини х (black-height) і позначати bh(x). Чорною висотою дерева будемо вважати чорну висоту його кореня.

Наступна лема показує, що червоно-чорні дерева ефективні як дерева пошуку.

Лема. Червоно-чорне дерево з n внутрішніми вершинами (тобто не враховуючи NIL-листків) має висоту не більше 2log(n+1).

• Тим самим для червоно-чорних дерев операції Search, Minimum, Maximum, Successor і Predecessor виконуються за час O(logn), тому що час їхнього виконання є O(h) для дерева висоти h, а червоно-чорне дерево з n вершинами має висоту O(logn).

• Стосовно процедур Tree-Insert і Tree-Delete проблема полягає в тому, що вони можуть зіпсувати структуру червоно-чорного дерева, порушивши RB-властивості. Тому ці процедури необхідно модифікувати. Нижче покажемо, що можна реалізувати додавання і видалення елементів за час O(logn) зі збереженням RB-властивостей.

• Операції Tree-Insert і Tree-Delete виконуються на червоно-чорному дереві за час O(logn), але змінюють дерево і відновлення його властивостей буде вимагати перефарбування деяких вершин і зміни структури дерева. Ми будемо змінювати структуру за допомогою обертань. Обертання становить собою локальну операцію (змінюється кілька вказівників) і зберігає властивість упорядкованості. На рис. показані два обертань: ліве і праве.

У процедурі лівого обертання (rotateLeft) передбачається, що x–>right != NULL (правий дочірній вузол вершини х не є листом). Ліве обертання виконується “навколо” зв’язку між х та у, роблячи у новим коренем піддерева, лівим дочірнім вузлом якого стає х, а бувший лівий потомок вузла у – правим потомком х.

void rotateLeft(T,x)

{ у = x–>right; //Знаходимо у.

x–>right = y–>left; //Ліве піддерево у стає правим піддеревом х.

if(y–>left != 0)

y–>left–>p = х;

y–>p = x–>p; // Робимо батька х батьком y

if (x–>p = = 0)

root[T] = у;

else if (x = = x–>p–>left)

x–>p–>left = у;

else x–>p–>right = у;

y–>left = x; // Робимо х лівою дитиною у.

x–>p = у; }

Процедура правого обертання rotateRight аналогічна. Обидві вони працюють за час O(1) і змінюють тільки вказівники. Інші поля вершин залишаються незмінними.

Додавання вершини в червоно-чорне дерево проводиться за час O(logn). Спочатку, як це робилося для двійкових дерев пошуку, ми застосовуємо процедуру insertNode, і фарбуємо нову вершину в червоний колір. Після цього треба відновити RB-властивості, для чого потрібно перефарбувати деякі вершини і виконати обертання. При цьому можливі різні ситуації. Розглянемо їх.

RB-INSERT(T, x)