Алгоритм (algorithm) — це формально описана обчислювальна процедура, яка отримує вхідні дані (input), що називаються входом алгоритму або його аргументом, і видає результат обчислень на вихід (output).

Таким чином, алгоритм являє собою послідовність обчислювальних кроків, що перетворюють вхідні величини на вихідні.

Алгоритми будують для розв’язання тих чи інших обчислювальних задач (computational problems). У постановці задачі у загальних рисах задається взаємодія між входом і виходом. В алгоритмі описується конкретна обчислювальна процедура, за допомогою якої вдається домогтися виконання зазначених взаємодій

Наприклад, відсортувати послідовності чисел в неспадному порядку.

Задача сортування (sorting problem) формально визначається наступним чином.

Вхід: послідовність з n чисел (а1, a2, ..., аn).

Вихід: перестановка (зміна порядку) (a1’, a2’, …, an’) вхідної послідовності таким чином, що для її членів виконується співвідношення a1’ ≤ a2’ ≤ … ≤ an’.

Алгоритм вважається коректним (correct), якщо для будь-якого допустимого входу він закінчує роботу і видає результат, який задовольняє вимогам задачі. В цьому випадку говорять, алгоритм розв'язує дану обчислювальну задачу. Якщо алгоритм некоректний, то для деяких входів він може взагалі не завершити свою роботу або видати неправильну відповідь.

Алгоритм може бути задано українською або англійською мовою, у вигляді комп'ютерної програми або навіть в машинних кодах – важливо лише , щоб процедура обчислень була чітко описана.

Властивості алгоритмів

• скінченність: алгоритм є скінченним об'єктом, що є необхідною умовою його механічної реалізованості;

• масовість: початкові дані для алгоритму можна вибирати із певної (можливо, нескінченної) множини даних; це означає, що алгоритм призначений не для однієї конкретної задачі, а для класу однотипних задач;

дискретність: розчленованість процесу виконання алгоритму на окремі кроки; це означає, що алгоритмічний процес здійснюється в дискретному часі

• елементарність: кожен крок алгоритму має бути простим, елементарним, можливість виконання якого людиною або машиною не викликає сумнівів;

• детермінованість: однозначність процесу виконання алгоритму; це означає, що при заданих початкових даних кожне дане, отримане на певному (не початковому) кроці, однозначно визначається даними, отриманими на попередніх кроках;

• результативність: алгоритм має засоби, які дозволяють відбирати із даних, отриманих на певному кроці виконання, результативні дані, після чого алгоритм зупиниться.

Insertion-Sort (A)

1 for j ← 2 to length [A]

2 do key ← A[j]

3 //Додати a[j] до відсортованої частини a[1..J-1].

4 i ← j-1

5 while i>0 and A [i]>key

6 do A[i+1] ← A [i]

7 i ← i-1

8 A[i+1] ← key

Ділянка А[1. . j-1] містить вже відсортовані елементи, а А[j+1. .n] — ще не переглянуті. У циклі for індекс j пробігає масив зліва направо. Беремо елемент A [j] (рядок 2 алгоритму) і пересуваємо ті елементи, що йдуть перед ним і більші за нього по величині (починаючи з (j-1)-го), вправо, звільняючи місце для взятого елементу (рядки 4-7). У рядку 8 елемент A[j] поміщається в звільнене місце.

Сортування вставками: аналіз

Час сортування вставками залежить від розміру сортованого масиву: чим більший масив, тим більше може знадобитися часу. Зазвичай вивчають залежності часу роботи від розміру входу. (Втім, для алгоритму сортування вставками важливий не лише розмір масиву, але й порядок його елементів: якщо масив майже впорядкований, то часу потрібно менше.)

Часом роботи (running time) алгоритму називаємо кількість елементарних кроків, які він виконує. Вважатимемо, що один рядок псевдокоду вимагає не більше фіксованої кількості операцій. Розрізнятимемо також виклик (call) процедури (на який припадає фіксована кількість операцій) і її виконання (execution), яке може бути довгим.

Позначимо біля кожного рядка його вартість (кількість операцій) і кількість разів, яку цей рядок виконується. Для кожного j від 2 до n (тут n = length[A] — розмір масиву) підрахуємо, скільки разів буде виконаний рядок 5, і позначимо це число через t_j . (Відмітимо, що рядки усередині циклу виконуються на один раз менше, ніж перевірка, оскільки остання перевірка виводить з циклу.)

1. for j ← 2 to length [A] с₁ n

2. do key ← A[j] с₂ n-1

3. //додати A[j] до відсортованої частини A[1..j-1]. 0 n-1

4. i ← j -1 с₄ n-1

5. while i>0 and A [i]>key с₅ ∑ⁿ_j=2 t_j

6. do A[i+1] ← A [i] с₆ ∑ⁿ_j=2 (t_j -1)

7. i ← i -1 с₇ ∑ⁿ_j=2 (t_j -1)

8 A[i+1] ← key с₈ n-1

Рядок вартості c, повторений т разів, дає внесок cm у загальну кількість операцій. Склавши внески всіх рядків, отримаємо:

Для процедури Insertion-Sort найбільш сприятливий випадок, коли масив вже відсортований. Тоді цикл в рядку 5 завершується вже після першої перевірки (оскільки А [i] ≤ key при i = j - 1), так що всі t_j рівні 1, і загальний час є

лінійна функція від n

Якщо ж масив розташований в зворотному (такому, що убуває) порядку, час роботи процедури буде максимальним: кожен елемент A[j] доведеться порівняти зі всіма елементами

А [1], ..., A[j - 1]. При цьому t_j = j. Оскільки

о тримуємо, що у найгіршому випадку час роботи процедури дорівнює

Квадратична функція від n

Побудова алгоритмів

Сортування вставками є прикладом алгоритму, що діє по крокам (incremental approach): ми додаємо елементи один за іншим до відсортованої частини масиву.

Розглянемо інший підхід, який називають «розділяй і володарюй» (divide-and-conquer approach), і побудуємо з його допомогою значно швидший алгоритм сортування.

Багато алгоритмів за природою рекурсивні (recursive algorithms): розв’язуючи деяку задачу, вони викликають самих себе для розв’язання її підзадач. Ідея методу «розділяй і володарюй» полягає як раз в цьому.

Принцип «розділяй і володарюй»

• Спочатку задача розбивається на декілька підзадач меншого розміру.

• Потім ці задачі розв’язуються (за допомогою рекурсивного виклику — або безпосередньо, якщо розмір досить малий).

• Нарешті, їх розв’язки комбінуються і отримується розв’язок вихідної задачі.

Принцип «розділяй і володарюй» для алгоритму сортування злиттям

• Спочатку ми розбиваємо масив на дві половини меншого розміру.

• Потім ми сортуємо кожну з половин окремо.

• Після цього нам залишається з'єднати два впорядковані масиви половинного розміру в один.

Рекурсивне розбиття задачі на менші відбувається до тих пір, поки розмір масиву не дійде до одиниці (будь-який масив довжини 1 можна вважати впорядкованим).

Процедура сортування злиттям Merge-Sort (A, p, r)

Сортує ділянку А[р.. r] масиву А, не змінюючи іншу частину масиву. При р>= r ділянка містить максимум один елемент, і є вже відсортованою.

В іншому випадку знаходимо число q, яке ділить ділянку на дві приблизно рівні частини А[р.. q] (містить én/2ù елементів) і A[q + 1..r] (містить ën/2û елементів).

ëхû - ціла частина х (найбільше ціле число, менше або рівне х),

éхù - найменше ціле число, більше або рівне х.

Процедура сортування злиттям Merge-Sort (A, p, r)

Merge-Sort (A, p, r)

1 if p<r

2 then q← ë(p+r)/2û

3 Merge-Sort (A, p, q)

4 Merge-Sort (A, q+1, r)

5 Merge (A, p, q, r)

Процедура Merge (A, p, q, r) –

допоміжна процедура з'єднання двох впорядкованих масивів в один.

П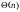 араметрами цієї процедури є масив А і числа р, q, r, що вказують на межі ділянок, які зливаються. Процедура передбачає, що р <= q < r і що ділянки А[р. .q] і A[q+1. .r] вже відсортовані, і зливає (merges) їх в одну ділянку А[р. .r].

Час роботи процедури Merge є , де n — загальна довжина ділянок, які зливаються (n = r - р+1).

Роботу процедури легко пояснити на картах. Нехай ми маємо дві стопки карт, і в кожній карти йдуть зверху вниз у зростаючому порядку.

Як зробити з них одну?

На кожному кроці беремо меншу з двох верхніх карт і кладемо її (сорочкою вверх) у результуючу стопку. Коли одна з вихідних стопок стає порожньою, ми додаємо карти другої стопки, які залишилися, до результуючої стопки. Зрозуміло, що кожен крок вимагає обмеженої кількості дій, і загальна кількість дій є .

Аналіз алгоритмів типу «розділяй і володарюй»

Як оцінити час роботи рекурсивного алгоритму? При підрахунку ми повинні врахувати час, що витрачається на рекурсивні виклики, так що виходить деяке рекурентне співвідношення (recurrence equation). Далі слід оцінити час роботи, виходячи з цього співвідношення.

Припустимо, що алгоритм розбиває задачу розміру n на а підзадач, кожна з яких має в b разів менший розмір. Вважатимемо, що розбиття вимагає часу D(n), а з'єднання отриманих розв’язків — часу С(n).

Тоді отримуємо співвідношення для часу роботи Т(n) на задачах розміру n (у найгіршому випадку):

Т(n) = аТ(n/b) + D(n) + С(n).

Аналіз сортування злиттям

Д ля простоти вважатимемо, що розмір масиву n є степенем двійки. Тоді на кожному кроці сортована ділянка ділиться на дві рівні половини. Розбиття на частини вимагає часу , а злиття — часу . Отримуємо співвідношення

з якого випливає T(n)=Θ(nlogn)

Тому для великих n сортування злиттям ефективніше, ніж сортування вставками, що вимагає часу Θ(n²).

Порівняння сортувань вставками і злиттям

Часто різниця між поганим і хорошим алгоритмом більш істотна, ніж між швидким і повільним комп'ютером. Нехай необхідно відсортувати масив з мільйона чисел.

• Що швидше — сортувати його вставками на швидшому комп'ютері А (мільярд інструкцій в секунду) або злиттям на повільнішому комп'ютері Б (лише десять мільйонів операцій в сек.)? Комп'ютер А працює в 100 разів швидше, ніж комп'ютер Б. Нехай до того ж сортування вставками написане на асемблері надзвичайно економно, і для сортування n чисел потрібно, скажімо, лише 2n² операцій. Водночас алгоритм злиттям написаний без особливої турботи про ефективність і вимагає 50nlogn операцій. Для сортування мільйона чисел отримуємо :

Аналізуючи будь-який алгоритм, можна намагатись знайти точну кількість дій, що виконує даний алгоритм. Але в більшості випадків достатньо оцінити асимптотику зростання часу роботи алгоритму при прямуванні розміру входу до нескінченності (asymptotic efficiency).

Якщо у одного алгоритму швидкість зростання менша, ніж у другого, то в більшості випадків він буде ефективнішим для всіх входів, крім зовсім коротких.

Час роботи алгоритму сортування методом вставки в найгіршому випадку виражається функцією T(n) = Θ (n²).

Для деякої функції g(n) запис Θ(g(n)) означає множину функцій

Функція f(n) належить множині Θ(g(n)), якщо існують додатні константи c₁ і c₂ такі, що дозволяють заключити цю функцію в рамки між функціями c₁g(n) і c₂g(n) для достатньо великих n.

- функція f(n) належить множині Θ(g(n))

Для всіх значень n>=n₀, функція f(n) більша або рівна функції c₁g(n), але не більша за функцію c₂g(n).

Функція g(n) є асимптотично

точною оцінкою функції f(n).

Означення Θ(g(n)) передбачає, що функції f(n) і g(n) асимптотично невід’ємні, тобто невід’ємні для достатньо великих значень n.

О-позначення

В Θ - позначеннях функція асимптотично обмежується зверху і знизу. Якщо ж достатньо визначити тільки асимптотичну верхню границю, використовуються О - позначення.

Для даної функції g(n) позначення О(g(n)) означає множину функцій таких, що

Щоб вказати, що функція f(n) належить множині О(g(n)), пишуть f(n) = О (g(n)).

Із випливає, що f(n) = О(g(n))

Для всіх значень n>=n₀, функція f(n) не перевищує значень функції cg(n).

Оскільки О-позначення описують верхню границю, то в ході їх використання для обмеження часу роботи алгоритму в найгіршому випадку отримуємо верхню границю цієї величини для будь-яких вхідних даних.

Ω-позначення

Аналогічно тому, як в О-позначеннях дається асимптотична верхня границя функції, в Ω-позначеннях дається її асимптотична нижня границя.

Для даної функції g(n) вираз Ω(g(n)) означає множину функцій таких, що

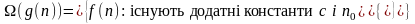
Щоб вказати, що функція f(n) належить множині Ω(g(n)), пишуть f(n) = Ω (g(n)).

Для всіх значень n>=n₀, значення функції f(n) більші або рівні значенням функції cg(n).

Коли говорять, що час роботи алгоритму дорівнює Ω(g(n)), при цьому мається на увазі, що незалежно від того, які вхідні дані вибрані для даного розміру n, при достатньо великих n час роботи алгоритму являє собою як мінімум константу, помножену на g(n).

Структури даних

Структура даних (data structure) — це спосіб зберігання і організації даних, який полегшує доступ до цих даних і їх модифікацію.

Множини, які змінюються в процесі виконання алгоритму, називаються динамічними.

Елемент динамічної множини — це запис, що містить різні поля. Часто одне з полів розглядається як ключ (key), призначений для ідентифікації елемента, а інші поля — як додаткова інформація (satellite data), що зберігається разом з ключем.

Елемент множини шукається за ключем.

Операції над динамічними множинами

Операції динамічної множини можна розбити на дві категорії: запити (queries), які просто повертають інформацію про множину, і операції-модифікатори (modifying operations), що змінюють множину.

Типові операції з множинами такі:

Search(S, к) (пошук). Запит, який за даною множиною S і ключем к повертає вказівник на елемент множини S з ключем к. Якщо такий елемент в множині S відсутній, повертається NIL.

Insert(S, x) Операція-модифікатор, яка поповнює задану множину S одним елементом, на який вказує х (мається на увазі, що до цього моменту всі поля в записі, на який вказує x, вже заповнені).

Delete(S, х) Операція-модифікатор, що видаляє із заданої множини S елемент, на який вказує х. (Зверніть увагу, що в цій операції використовується вказівник на елемент, а не його ключове значення.)

Minimum(S) Запит до повністю упорядкованої множини S, який повертає вказівник на елемент цієї множини з найменшим ключем.

Maximum(S) Запит до повністю впорядкованої множини S, який повертає вказівник на елемент цієї множини з найбільшим ключем.

Successor(S, x) (наступний) Запит до повністю впорядкованої множини S, що повертає вказівник на елемент множини S, ключ якого є найближчим сусідом ключа елемента х і перевищує його. Якщо ж х - максимальний елемент множини S, то повертається значення NIL.

Predecessor(S, x) (попередній) Запит до повністю впорядкованої множини S, що повертає вказівник на елемент множини S, ключ якого є найближчим меншим за значенням сусідом ключа елемента х. Якщо ж х - мінімальний елемент множини S, то повертається значення NIL.

Розглянемо різні структури даних (списки, стеки, черги, кореневі дерева), призначені для роботи з динамічними множинами.

Зв’язний список (linked list) — це структура даних, у якій об’єкти розташовані у лінійному порядку. Однак, на відміну від масиву, у якому цей порядок визначається індексами, порядок у зв’язному списку визначається вказівниками на кожен об’єкт.

Зв’язні списки забезпечують просте й гнучке представлення динамічних множин і підтримують вище перераховані операції.

У двічі зв’язному списку L (у двозв'язному)(doubly linked list) кожен елемент являє собою об’єкт з одним полем ключа key та двома полями-вказівниками: next (наступний) і prev (попередній).

Цей об’єкт може також містити інші супутні дані.

Для заданого елемента списку х вказівник next [x] вказує на наступний елемент зв'язаного списку, а вказівник prev [x] — на попередній.

Якщо prev [х] = NIL, у елемента х немає попереднього, і, отже, він є першим, тобто головним у списку.

Якщо next [x] = NIL, то у елемента х немає наступного, тому він є останнім, тобто хвостовим у списку.

head [L] - вказівник на перший елемент списку. Якщо head [L] = =NIL, то список порожній.

Перш ніж рухатися по вказівниках, треба знати хоча б один елемент списку; передбачаємо, що для списку L відомий вказівник head[L] на його голову.

Двосторонньо зв'язаний список L містить числа 1, 4, 9, 16. Кожен елемент списку — це запис з полями для ключа і вказівників на попередній та наступний елементи (ці вказівники позначені стрілками). У полі next в хвості списку і в полі prev в голові списку знаходиться вказівник NIL (коса риска на схемі); head[L] вказує на голову списку

Списки можуть бути різних видів. Список може бути однократно або двічі зв'язним, відсортованим або невідсортованим, кільцевим або некільцевим.

Якщо список однократно зв'язаний (однонаправлений) (singly linked), то вказівник prev в його елементах відсутній.

Якщо список відсортований (sorted), то його лінійний порядок відповідає лінійному порядку його ключів; у цьому випадку мінімальний елемент знаходиться в голові списку, а максимальний — у його хвості.

Якщо список невідсортований, то його елементи можуть розташовуватися в довільному порядку.

Якщо список кільцевий (circular list), то вказівник prev його головного елементу вказує на його хвіст, а вказівник next хвостового елементу — на головний елемент. Такий список можна розглядати як замкнутий у вигляді кільця набір елементів.

Пошук у зв’язному списку

Процедура List_Search(L, k) дозволяє знайти у списку L перший елемент з ключем k шляхом лінійного пошуку, і повертає вказівник на знайдений елемент. Якщо елемент з ключем k у списку відсутній, повертається значення nil.

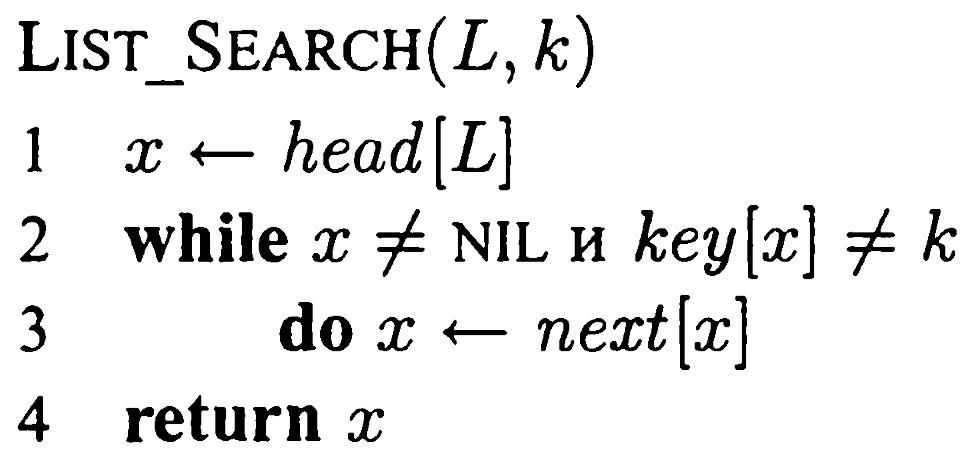
Додавання елемента у список

Якщо є елемент х, полю key якого заздалегідь надано значення, то процедура List-Insert вставляє елемент х у голову списку

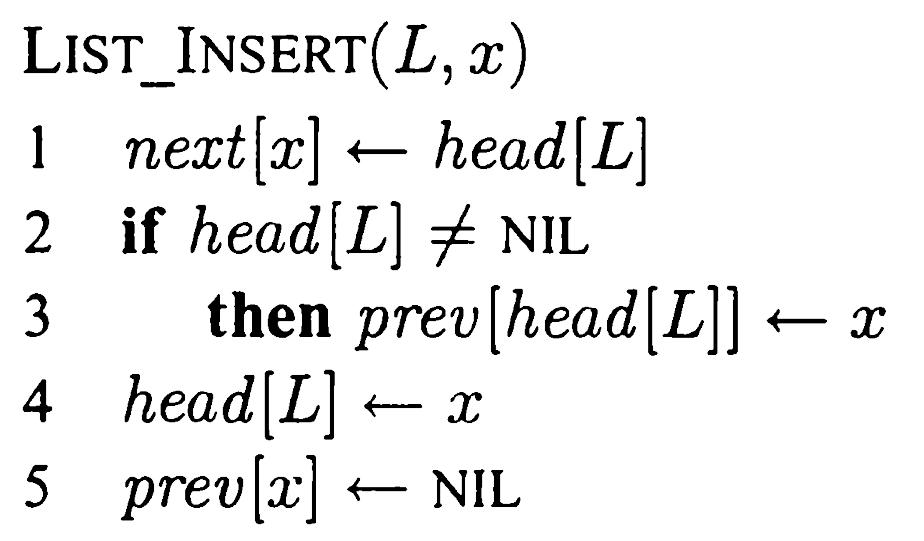
Час роботи процедури List-Insert дорівнює О(1) (не залежить від довжини списку).

Видалення елементу зі списку

Процедура List_Delete видаляє елемент х зі зв'язного списку L. У процедуру передається вказівник на елемент х, після чого вона видаляє х зі списку шляхом оновлення вказівників. (Щоб видалити елемент із заданим ключем, необхідно спочатку викликати процедуру List_Search для отримання вказівника на елемент.)

Час роботи процедури List_Delete дорівнює О(1), але якщо потрібно видалити елемент із заданим ключем, то в найгіршому випадку знадобиться час O(n), оскільки спочатку необхідно викликати процедуру List_Search.