Обработка информации Математические проблемы реализации алгоритмов на эвм

Для решения системной задачи данные о системе объекта необходимо физически закодировать. Общим способом кодирования данных является их представление в виде энергетических уровней величиной ΔЕ. Число энергетических уровней равно N = E/ΔE, где Е — энергия системы, которой мы располагаем. Максимальное число физически разрешимых уровней для заданного количества энергии определяется принципом неопределенности Гейзенберга, согласно которому величина уровня должна удовлетворять условию

ΔE•Δt h, где Δt — длительность интервала наблюдения h = 6,63•10^-27 эрг*c — постоянная Планка.

Из этого следует:

N E•Δt/h

Тогда с учетом формулы Энштейна Е = mc^2 получим:

N mc^2•Δt/h

Отсюда следует, что измеритель массой 1 г за время 1 с может обработать не более N = 1,36•10^47 бит данных.

Представим гипотетический измеритель массой, равной массе Земли m = 6•10^27 г. Этот измеритель за время, равное примерно времени существования Земли q =10^10 лет смог бы обработать порядка 10^93 бит данных. Это число обычно называют пределом Бреммермана.

Задачи, требующие обработки более чем 10^93 бит информации называются трансвычислительными задачами. К сожалению, комбинаторика говорит нам, что такой предел может быть достигнут для задач даже относительно небольшого размера.

Например, в распознавании образов: пусть есть массив q*q, каждый элемент которого может быть раскрашен одним из k цветов, тогда всего вариантов раскраски может быть k^(q*q). Если массив 18×18, то задача трансверсальна при двух цветах. Так же 67! > 10^94.

Реальные вычислительные мощности

Процессоры персональных компьютеров

AMD AMD ATHLON II X4 645 3.1 ГГц (2010) — 38.44 Гфлопс

Мощнейший компьютер на 2011 K computer 10,51 * 10^15 FLOPS

В одних сутках 86400 секунд ~ 10^5

За сутки вычислений персональный 10^15, суперкомпьютер 10^20

Год работы +2 порядка

Закон Мура: число транзисторов на кристалле будет удваиваться каждые 24 месяца.

Теория алгоритмов

формальное доказательство алгоритмической неразрешимости задач,

асимптотический анализ сложности алгоритмов

классификация алгоритмов в соответствии с классами сложности,

разработка критериев сравнительной оценки качества алгоритмов

1. алгоритмической неразрешимости задач

разрешимость свойство формальной теории(задачи) обладать алгоритмом, определяющим, выводима она из множества аксиом данной теории или нет. Теория называется разрешимой, если такой алгоритм существует, и неразрешимой, в противном случае.

Изначально вопрос разрешимости решали простым нахождением алгоритма. Если же алгоритм не находится, возможно его не существует и это тогда требуется строго доказать. А для этого нужно точно знать, что такое алгоритм.

модель вычислений описывает множество допустимых операций, использованных для вычисления, а также относительных издержек их применения.

Если выбрана определённая модель вычислений можно охарактеризовать необходимые вычислительные ресурсы (время выполнения, объём памяти) а также ограничения алгоритмов или компьютера.

абстрактные машины (абстрактные вычислители), используемые для доказательства вычислимости и получения верхней границы вычислительной сложности алгоритма и модели принятия решений

Гильберта Гёдель впервые описал класс так называемых рекурсивных функций. Впоследствии был введён ряд других формализмов, таких как машина Тьюринга, λ-исчисление, оказавшихся эквивалентными рекурсивным функциям.

К примеру задача определяется какой то функцией f. Эту задачу программирования называют алгоритмически разрешимой или алгоритмически неразрешимой, в зависимости от того, является функция f вычислимой или нет.

Тезис Чёрча — Тьюринга

формулируется как совпадение классов вычислимых и частично рекурсивных функций

гласит, что для любой интуитивно вычислимой функции существует вычисляющая её значения машина Тьюринга.

физический тезис Чёрча — Тьюринга: любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга;

Сильный тезис Чёрча — Тьюринга (тезис Чёрча — Тьюринга — Дойча): любой конечный физический процесс, не использующий аппарат, связанный с непрерывностью и бесконечностью, может быть вычислен физическим устройством.

машиной Тьюринга, которая оперирует лишь с вычислимыми объектами.

Теоре́ма Гёделя о неполноте́ и втора́я теоре́ма Гёделя— две теоремы математической логики о принципиальных ограничениях формальной арифметики

Дойч предположил, что квантовые компьютеры смогут превозмочь ограничения данного принципа, если алгебраические законы квантовой физики смогут стать теоретической базой, описывающей любые физические процессы.

Термин рекурсивная функция в теории вычислимости используется для обозначения трёх классов функций

примитивно рекурсивные функции;

частично рекурсивные функции.

общерекурсивные функции;

Множество частично рекурсивных функции включает в себя множество общерекурсивных функции, а общерекурсивные функции включают в себя примитивно рекурсивные функции. Частично рекурсивные функции иногда называют просто рекурсивными функциями.

Класс примитивно рекурсивных функций описывается минимумом операций, в нем можно реализовать такие действия как сложение умножение и т.д.

Класс общерекурсивных функций описан расширенным набором операций и соответствуют программным блокам, в которых используется только арифметические операции, а также условный оператор и оператор арифметического цикла (оператор цикла, в котором число итераций известно на момент начала цикла)

Частично рекурсивные функции для некоторых значений аргумента могут быть не определены.

Общерекурсивная функция — частично рекурсивная функция, определённая для всех значений аргументов

временная сложность - время работы алгоритма (минимальное среднее или максимальное)

пространственная сложность - объем используемой памяти

Рассмотрение входных данных большого размера и оценка порядка роста времени работы алгоритма приводят к понятию асимптотической сложности алгоритма.

Запись вида f(n) = O(g(n)) означает, что ф-ия f(n) возрастает медленнее чем ф-ия g(n) т.е. существует такая "с" что для все n c*g(n) >=f(n)

Таким образом O – означает верхнее ограничение сложности алгоритма.

f(n) = O(1) константа

f(n) = O(log(n)) логарифмический рост

f(n) = O(n) линейный рост

f(n) = O(n*log(n)) квазилинейный рост

f(n) = O(n^m) полиномиальный рост

f(n) = O(2^n) экспоненциальный рост

Правила для определения сложности

1. O(k*f) = O(f)

2. O(f*g) = O(f)*O(g) или O(f/g) = O(f)/O(g)

3. O(f+g) равна доминанте O(f) и O(g)

Здесь k обозначает константу, a f и g - функции.

Увеличение скорости вычислений влияет на коэффициент в функции роста. В определенных масштабах это будет давать значительный прирост эффективности, но при увеличении размерности входных данных этот выигрыш может быстро нивелироваться скорость роста функции.

Какие либо методы с уменьшением размерности тоже не всегда будут иметь значимый эффект. Разобьем наш массив на 4 части и каждую часть поручим выполнять отдельному ядру. Что мы получим? На сортировку каждой части понадобится ровно O((n / 4)^2). Возведем получившееся выражение в квадрат, получив таким образом сложность равную O(1/16*n^2 + n),

Поскольку анализ у нас асимптотический, то при достаточно больших n, ф-ия n^2 будет вносить гораздо больший вклад в итоговый результат, чем n и поэтому мы спокойно можем им пренебречь, как наиболее медленно возрастающем членом, также за малозначимостью принебрегаем коэффициентом 1/16, что в итоге дает нам все тоже O(n^2).

Небольшие размерности входных данных:

Сложность f=10x при нормальных размерах входных данных лучше g=x^2. Но при размерах <10 первый алгоритм эффективнее.

f является «о» малым от g, если для любого ε > 0 найдутся значения х при которых

x^2 = o(x)

x^2 < ε *x при х< ε

Хотя f=x^2 растет быстрее g=x, в некоторых случаях εx>x^2 для любых коэффициентов.

Грубо говоря в применении к алгоритмам в данном случае функция с большей скоростью роста эффективна при малой размерности входных данных, и коэффициентами этого не поправить.

На определенном интервале коэффициенты влияют значительнее, чем зависимость от входных данных, или наоборот. Поэтому в каждом конкретном случае нужно смотреть что эффективнее, улучшать коэффициенты или зависимость от входа.

Амортизационный анализ применяется для оценки времени выполнения нескольких операций с какой-либо структурой данных (например, стеком). Чтобы оценить время выполнения какой-либо последовательности операций, достаточно умножить максимальную длительность операции на общее число операций. Иногда, однако, удаётся получить более точную оценку времени выполнения последовательности операций (или, что равносильно, среднего времени выполнения одной операции), используя тот факт, что во многих случаях после длительных операций несколько следующих операций выполняются быстро. Оценки такого рода называются амортизационным анализом (amortized analysis) структуры данных (точнее, её реализации).

Классы сложности:

В теории алгоритмов классами сложности называются множества вычислительных задач, примерно одинаковых по сложности вычисления. (P-сложные, экспоненциально сложные и др.).

Для каждого класса существует категория задач, которые являются «самыми сложными». Это означает, что любая задача из класса сводится к такой задаче, и притом сама задача лежит в классе. Такие задачи называют полными задачами для данного класса. Полные задачи — хороший инструмент для доказательства равенства классов. Достаточно для одной такой задачи предоставить алгоритм, решающий её и принадлежащий более маленькому классу, и равенство будет доказано.

К классу P относятся задачи, которые могут быть решены за время, полиномиально зависящее от объёма исходных данных, с помощью детерминированной вычислительной машины (например, машины Тьюринга).

NP — задачи, которые могут быть решены за полиномиально выраженное время с помощью недетерминированной вычислительной машины, то есть машины, следующее состояние которой не всегда однозначно определяется предыдущими. Работу такой машины можно представить как разветвляющийся на каждой неоднозначности процесс: задача считается решённой, если хотя бы одна ветвь процесса пришла к ответу.

Другое определение класса NP: к классу NP относятся задачи, решение которых мы можем проверить за полиномиальное время.

В общем случае нет оснований полагать, что для той или иной NP-задачи не может быть найдено P-решение. Вопрос о возможной эквивалентности классов P и NP (то есть о возможности нахождения P-решения для любой NP-задачи) считается многими одним из основных вопросов современной теории сложности алгоритмов.

Сама постановка вопроса об эквивалентности классов P и NP возможна благодаря введению понятия NP-полных задач. NP-полные задачи составляют подмножество NP-задач и отличаются тем свойством, что все NP-задачи могут быть тем или иным способом сведены к ним.

Из этого следует, что если для NP-полной задачи будет найдено P-решение, то P-решение будет найдено для всех задач класса NP. Это будет означать, что все задачи, принадлежащие классу NP, можно будет решать за полиномиальное время, что сулит огромную выгоду с вычислительной точки зрения. Сейчас NP-полные задачи можно решить за экспоненциальное время, что почти всегда неприемлемо.

В августе 2010 года Винэй Деолаликар разослал некоторым ученым на проверку своё доказательство неравенства P и NP. Стивен Кук назвал его «относительно серьезной попыткой решения проблемы P vs NP». Однако уже в том же месяце были найдены недостатки в доказательстве. Сейчас оно дорабатывается.

Обобщение детерминированной машины Тьюринга, в которой, из любого состояния и значений на ленте, машина может совершить один из нескольких (можно считать, без ограничения общности — двух) возможных переходов, а выбор осуществляется вероятностным образом (подбрасыванием монетки)

В теории алгоритмов классом сложности BPP (от англ. bounded-error, probabilistic, polynomial) называется класс предикатов, быстро (за полиномиальное время) вычислимых и дающих ответ с высокой вероятностью (причём, жертвуя временем, можно добиться сколь угодно высокой точности ответа). Задачи, решаемые вероятностными методами и лежащие в BPP, возникают на практике очень часто.

Это верно, поскольку если есть машина Тьюринга, распознающая язык с вероятностью ошибки p за время O(n^k), то точность можно сколь угодно хорошо улучшить за счёт относительно небольшого прироста времени. Если мы запустим машину n раз подряд, а в качестве результата возьмём результат большинства запусков, то вероятность ошибки значительно упадёт, а время станет равным O(n^k+1).

В теории алгоритмов классом сложности BQP (от англ. bounded error quantum polynomial time) называется класс проблем разрешимости, которые могут быть решены квантовым компьютером за полиномиальное время

Вопрос о существовании алгоритма факторизации с полиномиальной сложностью на классическом компьютере является одной из важных открытых проблем современной теории чисел. В то же время факторизация с полиномиальной сложностью возможна на квантовом компьютере с помощью алгоритма Шора (класс BQP).

Предполагаемая большая вычислительная сложность задачи факторизации лежит в основе криптостойкости некоторых алгоритмов шифрования с открытым ключом, таких как RSA.

Полный перебор

Метод ветвей и границ

Для ускорения перебора метод ветвей и границ использует отсев подмножеств допустимых решений, заведомо не содержащих оптимальных решений.

Распараллеливание вычислений

...

Динамическое программирование

разбиение задачи на последовательность простых

и оптимизация за счет выполнения каждой задачи только один раз

Эвристические алгоритмы

Эвристический алгоритм (эвристика) — алгоритм решения задачи, не имеющий строгого обоснования, но, тем не менее, дающий приемлемое решение задачи в большинстве практически значимых случаев.

эвристика, в отличие от корректного алгоритма решения задачи, обладает следующими особенностями:

Она не гарантирует нахождение лучшего решения.

Она не гарантирует нахождение решения, даже если оно заведомо существует (возможен «пропуск цели»).

Она может дать неверное решение в некоторых случаях.

Приближенные алгоритмы

...

В областях искусственного интеллекта, таких, как распознавание образов, эвристические алгоритмы широко применяются также и по причине отсутствия общего решения поставленной задачи. Различные эвристические подходы применяются в антивирусных программах, компьютерных играх и т. д

Системы компьютерной алгебры

Система компьютерной алгебры (СКА, англ. computer algebra system, CAS) — это приложение, помогающее выполнять символьные вычисления. Основная задача СКА — это работа с математическими выражениями в аналитической (символьной) форме.

Аналитическое вычисление не сталкивается с такими проблемами численного программирования как ошибки округления, проблемы сходимости и проблемы устойчивости.

Основными проблемами самого процесса вычисления является чаще всего экспоненциальное время работы алгоритмов и промежуточное разрастание выражения во время вычислений

Среди различных вариантов выбранного процесса вычисления можно отметить два следующих, а именно, полное рекурсивное вычисление выражения и метод отложенных вычислений.

Data Mining

Развитие методов записи и хранения данных привело к бурному росту объемов собираемой и анализируемой информации. Объемы данных настолько внушительны, что человеку просто не по силам проанализировать их самостоятельно, хотя необходимость проведения такого анализа вполне очевидна, ведь в этих "сырых" данных заключены знания, которые могут быть использованы при принятии решений. Для того чтобы провести автоматический анализ данных, используется Data Mining.

Data Mining – это процесс обнаружения в "сырых" данных ранее неизвестных нетривиальных практически полезных и доступных интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности.

Методы Data Mining лежат на стыке баз данных, статистики и искусственного интеллекта

Задачи, решаемые методами Data Mining, принято разделять на

описательные (англ. descriptive);

предсказательные (англ. predictive).

В описательных задачах самое главное — это дать наглядное описание имеющихся скрытых закономерностей, в то время как в предсказательных задачах на первом плане стоит вопрос о предсказании для тех случаев, для которых данных ещё нет.

Задачи, решаемые методами Data Mining:

1. Классификация – это отнесение объектов (наблюдений, событий) к одному из заранее известных классов.

2. Регрессия, в том числе задачи прогнозирования. Установление зависимости непрерывных выходных от входных переменных.

3. Кластеризация – это группировка объектов (наблюдений, событий) на основе данных (свойств), описывающих сущность этих объектов. Объекты внутри кластера должны быть "похожими" друг на друга и отличаться от объектов, вошедших в другие кластеры. Чем больше похожи объекты внутри кластера и чем больше отличий между кластерами, тем точнее кластеризация.

4. Ассоциация – выявление закономерностей между связанными событиями. Примером такой закономерности служит правило, указывающее, что из события X следует событие Y. Такие правила называются ассоциативными. Впервые эта задача была предложена для нахождения типичных шаблонов покупок, совершаемых в супермаркетах, поэтому иногда ее еще называют анализом рыночной корзины (market basket analysis).

5. Последовательные шаблоны – установление закономерностей между связанными во времени событиями, т.е. обнаружение зависимости, что если произойдет событие X, то спустя заданное время произойдет событие Y.

6. Анализ отклонений – выявление наиболее нехарактерных шаблонов.

Data Mining основаны на применении

1. деревьев решений,

2. нейронных сетей, нечеткой логики.

3. генетических алгоритмов, эволюционного программирования,

4. ассоциативной памяти,

Деревья принятия решений обычно используются для решения задач классификации данных или, иначе говоря, для задачи аппроксимации заданной булевой функции.

Дерево принятия решений — это дерево, на ребрах которого записаны атрибуты, от которых зависит целевая функция, в листьях записаны значения целевой функции, а в остальных узлах — атрибуты, по которым различаются случаи. Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение.

Предположим, что нас интересует, выиграет ли наша любимая футбольная команда следующий матч. Мы знаем, что это зависит от ряда параметров; перечислять их все — задача безнадежная, поэтому ограничимся основными:

1. выше ли находится соперник по турнирной таблице;

2. дома ли играется матч;

3. пропускает ли матч кто-либо из лидеров команды;

4. идет ли дождь.

Современные проблемы развития элементной базы

http://compblog.ilc.edu.ru/blog/63.html

• Квантовый компьютер

• Механический компьютер

• Оптический компьютер

• Электронный компьютер

• Биологический компьютер

переход к конструированию ЭВМ на СБИС и ультраСБИС должен сопровождаться снижением тактовой частоты работы схемы. Дальнейший прогресс в повышении производительности может быть обеспечен либо за счет архитектурных решений, либо за счет новых принципов построения и работы микросхем.

Проблемы развития элементной базы:

Новые литографии и сверхточные материалы Степень микроминиатюризации, размер кристалла ИС, производительность и стоимость технологии напрямую определяется типом литографии. 5-10 лет назад доминировала оптическая литография. Дальнейшие успехи связаны с электронной (лазерной), ионной и рентгеновской литографией. Послойные рисунки на моторезисторе микросхем наносились световым лучом, а эта литография позволяла получить более тонкий луч.

Сверхчистые материалы и высоковакуумные технологии Микроскопическая толщина линий, сравнимая с диаметром молекул, требует высокой чистоты используемых и напыляемых материалов, применения вакуумных установок и снижения рабочих температур. Поэтому новые заводы по производству микросхем представляют собой уникальное оборудование, размещаемое в “сверхчистых” помещениях.

Борьба с потребляемой и рассеиваемой мощностью Уменьшение линейных размеров микросхем и повышение уровня их интеграции заставляют проектировщиков искать средства борьбы с потребляемой( ) и рассеиваемой( ) мощностью. При сокращении линейных размеров микросхем в 2 раза, их объёмы изменяются в 8 раз. Пропорционально этим цифрам должны меняться значения и , иначе схемы будут перегреваться и выходить из строя. За последние 10 лет быстродействия процессоров Intel выросло в 5-6 раз, а энергопотребление в 18 раз. Напряжение линейных микросхем упало до 1,5V и менее, а напряжение питания новейших многоядерных микропроцессов Intel = 1,35V. Дальнейшее понижение нежелательно, так как в электронных схемах всегда должно быть обеспечено необходимое соотношение “сигнал-шум”, характеризующее устойчивую работу компьютера. Протекание тока по микроскопическим проводникам сопряжено с выделением большого количества тепла. Поэтому, создавая сверхбольшие интегральные схемы, проектировщики вынуждены снижать тактовую частоту работы процессора. Дальнейший прогресс в повышении производительности может быть обеспечен либо за счёт архитектурных решений, либо за счёт новых принципов построения и работы микросхем.

Пути развития элементарной базы:

Создание молекулярных компьютеров и биокомпьютеров

Во многих странах проводятся опыты по синтезу молекул на основе их стереохимического генетического кода, способных менять ориентацию и реагировать на воздействия током, светом и т.п. Например, ученые фирмы Hewlett-Packard и Калифорнийского университета (UCLA) доказали принципиальную возможность создания молекулярной памяти ЭВМ на основе молекул роксана (http://www.zdnet.ru/printreviews.asp?ID=89). Продолжаются работы по созданию логических схем, узлов и блоков. По оценкам ученых, подобный компьютер в 100 млрд раз будет экономичнее современных микропроцессоров.

вычислительные системы, использующие вычислительные возможности молекул (преимущественно, органических). Молекулярными компьютерами используется идея вычислительных возможностей расположения атомов в пространстве.

Под молекулярным компьютером обычно понимают такие системы, которые используют отдельные молекулы в качестве элементов вычислительного тракта. В частности, молекулярный компьютер может представлять логические электрические цепи, составленные из отдельных молекул; транзисторы, управляемые одной молекулой, и т.п.

ДНК-компьютер

Также молекулярным компьютером могут назвать ДНК-компьютер, вычисления в котором соответствуют различным реакциям между фрагментами ДНК. От классических компьютеров такие отличаются тем, что химические реакции происходят сразу между множеством молекул независимо друг от друга.

В 1994 году Леонард Адлеман, профессор университета Южной Калифорнии, продемонстрировал, что с помощью пробирки с ДНК можно весьма эффективно решать классическую комбинаторную «задачу о коммивояжере» (кратчайший маршрут обхода вершин графа). Классические компьютерные архитектуры требуют множества вычислений с опробованием каждого варианта.

Метод ДНК позволяет сразу сгенерировать все возможные варианты решений с помощью известных биохимических реакций. Затем возможно быстро отфильтровать именно ту молекулу-нить, в которой закодирован нужный ответ.

Проблемы, возникающие при этом:

Требуется чрезвычайно трудоёмкая серия реакций, проводимых под тщательным наблюдением.

Существует проблема масштабирования задачи.

Биокомпьютер Адлемана отыскивал оптимальный маршрут обхода для 7 вершин графа. Но чем больше вершин графа, тем больше биокомпьютеру требуется ДНК-материала.

Было подсчитано, что при масштабировании методики Адлемана для решения задачи обхода не 7 пунктов, а около 200, масса количества ДНК, необходимого для представления всех возможных решений превысит массу нашей планеты.

Нейрокомпьютеры.

Нейрокомпьютер — устройство переработки информации на основе принципов работы естественных нейронных систем.[1] Эти принципы были формализованы, что позволило говорить о теории искусственных нейронных сетей. Проблематика же нейрокомпьютеров заключается в построении реальных физических устройств, что позволит не просто моделировать искусственные нейронные сети на обычном компьютере, но так изменить принципы работы компьютера, что станет возможным говорить о том, что они работают в соответствии с теорией искусственных нейронных сетей.

Три основных преимущества нейрокомпьютеров:

Все алгоритмы нейроинформатики высокопараллельны, а это уже залог высокого быстродействия.

Нейросистемы можно легко сделать очень устойчивыми к помехам и разрушениям.

Устойчивые и надёжные нейросистемы могут создаваться и из ненадёжных элементов, имеющих значительный разброс параметров.

Оптические компьютеры

Способность света параллельно распространяться в пространстве даёт возможность создавать параллельные устройства обработки. Это позволило бы ускорить быстродействие компьютеров. Проводятся эксперименты по проектированию оптоэлектронных и оптонейронных отдельных устройств. В связи с появлением многоядерных процессоров возникла проблема оперативного обмена данными между ядрами. Появились работы, связанные с буферизацией световых сигналов, с использованием устройств торможения света. Это позволяет использовать в компьютерах коммутационные световые элементы для достижения более высокой производительности.

Квантовые компьютеры

Принцип работы элементов квантового компьютера основан на способности электрона в атоме иметь различные уровни энергии: Е0, Е1,..., Еп. Переход электрона с нижнего энергетического уровня на более высокий связан с поглощением кванта электромагнитной энергии — фотона. При излучении фотона осуществляется обратный переход. Всеми подобными переходами можно управлять, используя действие электромагнитного поля от атомного или молекулярного генератора. Этим исключаются спонтанные переходы с одного уровня на другой. Основным же строительным блоком квантового компьютера служит qubit — Quantum Bit, который может иметь большое число состояний. Для таких блоков определен логически полный набор элементарных функций.

Ква́нтовая телепорта́ция — передача квантового состояния на расстояние. Квантовая телепортация не передаёт энергию или вещество на расстояние. Обязательным этапом при квантовой телепортации является передача информации между точками отправления и приёма по классическому, неквантовому каналу, которая может осуществляться не быстрее, чем со скоростью света, тем самым не нарушая принципов современной физики.

Пусть у отправителя есть частица А, находящаяся в произвольном квантовом состоянии ψA = αψ1 + βψ2, и он хочет передать это квантовое состояние получателю, то есть сделать так, чтобы у получателя оказалась в распоряжении частица B в том же самом состоянии. Иными словами, необходимо передать отношение двух комплексных чисел α и β

Отправитель и получатель договариваются заранее о создании пары квантово-запутанных частиц C и B, причём C попадёт отправителю, а B — получателю.

Квантовая система частиц A и C имеет четыре состояния, однако мы не можем описать её состояние вектором — чистым (полностью определённым) состоянием обладает лишь система из трёх частиц A, B, C. Когда отправитель совершает измерение, имеющее четыре возможных исхода, над системой из двух частиц A и C, он получает одно из 4 собственных значений измеряемой величины. Поскольку при этом измерении система из трёх частиц A, B, C коллапсирует в некое новое состояние, причём состояния частиц A и C становятся известны полностью, то сцепленность разрушается и частица B оказывается в некотором определённом квантовом состоянии.

Именно в этот момент происходит как бы "передача" «квантовой части» информации. Однако восстановить передаваемую информацию пока невозможно: получатель знает, что состояние частицы B как-то связано с состоянием частицы A, но не знает как именно.

Для выяснения этого необходимо, чтобы отправитель сообщил получателю по обычному классическому каналу результат своего измерения (затратив при этом два бита, соответствующие зацепленному состоянию AC, измеренному отправителем). По законам квантовой механики получается, что имея результат измерения, проведённого над парой частиц A и C и плюс к тому запутанную с C частицу B, получатель сможет совершить необходимое преобразование над состоянием частицы B и восстановить исходное состояние частицы A.

http://ru.wikipedia.org/wiki/ Квантовая_телепортация

Куби́т (q-бит, кьюбит; от quantum bit) — квантовый разряд или наименьший элемент для хранения информации в квантовом компьютере .

Как и бит, кубит допускает два собственных состояния, обозначаемых |0\ и |1\ (обозначения Дирака), но при этом может находиться и в их суперпозиции, то есть в состоянии , где A и B любые комплексные числа, удовлетворяющие условию | A | 2 + | B | 2 = 1.

При любом измерении состояния кубита он случайно переходит в одно из своих собственных состояний. Вероятности перехода в эти состояния равны, соответственно | A | 2 и | B | 2,

Имеется кубит в квантовом состоянии

В этом случае, вероятность получить при измерении

0 составляет (4/5)²=16/25 = 64 %,

1 (-3/5)²=9/25 = 36 %.

В данном случае, при измерении мы получили 0 с 64 % вероятностью.

В результате измерения кубит переходит в новое квантовое состояние , то есть, при следующем измерении этого кубита мы получим 0 со стопроцентной вероятностью

Перейдем к системе из двух кубитов. Измерение каждого из них может дать 0 или 1. Поэтому у системы есть 4 классических состояния: 00, 01, 10 и 11. Аналогичные им базовые квантовые состояния: . И наконец, общее квантовое состояние системы имеет вид . Теперь |a|² — вероятность измерить 00 и т. д. Отметим, что |a|²+|b|²+|c|²+|d|²=1 как полная вероятность.

Если мы измерим только первый кубит квантовой системы, находящейся в состоянии , у нас получится:

С вероятностью p₀ = | a | ² + | b | ² первый кубит перейдет в состояние а второй — в состояние 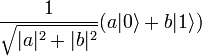, а

С вероятностью p₁ = | c | ² + | d | ² первый кубит перейдет в состояние а второй — в состояние .

http://ru.wikipedia.org/wiki/Квантовый_компьютер

Кубиты могут быть связаны друг с другом, то есть, на них может быть наложена ненаблюдаемая связь, выражающаяся в том, что при всяком измерении над одним из нескольких кубитов, остальные меняются согласованно с ним. То есть, совокупность запутанных между собой кубитов может интерпретироваться как заполненный квантовый регистр. Как и отдельный кубит, квантовый регистр гораздо более информативен. Он может находиться не только во всевозможных комбинациях составляющих его битов, но и реализовывать всевозможные тонкие зависимости между ними.

Несмотря на то, что мы сами не можем непосредственно наблюдать состояние кубитов и квантовых регистров во всей полноте, между собой они могут обмениваться своим состоянием и могут его преобразовывать. Тогда есть возможность создать компьютер, способный к параллельным вычислениям на уровне своего физического устройства и проблемой остаётся лишь прочитать конечный результат вычислений.

http://ru.wikipedia.org/wiki/Кубит

Результат работы квантового алгоритма носит вероятностный характер. [1] За счет небольшого увеличения количества операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице.

Главный тип задач, которые ускоряются квантовыми алгоритмами, являются задачи типа перебора. Их можно разделить на 2 основные группы:

Задачи моделирования динамики сложных систем (первоначальная идея Фейнмана) и

Математические задачи, сводящиеся к перебору вариантов.

Квантовое вычисление является процессом особого рода. Оно использует особый физический ресурс: квантовые запутанные состояния, что позволяет в некоторых случаях достигнуть поразительного выигрыша во времени. Такие случаи называются квантовым ускорением классических вычислений. Случаи квантового ускорения, на фоне общей массы классических алгоритмов, редки.

Если классический процессор в каждый момент может находиться ровно в одном из состояний , (обозначения Дирака) то квантовый процессор в каждый момент находится одновременно во всех этих базисных состояниях, при этом в каждом состоянии |j\rangle — со своей комплексной амплитудой λj. Это квантовое состояние называется «квантовой суперпозицией» данных классических состояний и обозначается как

Квантовое состояние может изменяться во времени двумя принципиально различными путями:

Унитарная квантовая операция (квантовый вентиль, англ. quantum gate), в дальнейшем просто операция.

Измерение (наблюдение).

В основе квантового параллелизма лежит использование при вычислениях суперпозиций базовых состояний, что позволяет одновременно производить большое количество вычислений с различными исходными данными. Например, 64-разрядный квантовый регистр может хранить до 264 значений одновременно [1][2], а квантовый компьютер может все эти значения одновременно обрабатывать

Реализация квантовых вычислителей.

Двум значениям кубита могут соответствовать, например, основное и возбужденное состояния атома, направления вверх и вниз спина атомного ядра, направление тока в сверхпроводящем кольце, два возможных положения электрона в полупроводнике и т.п.

Одно- или двухкубитовые квантовые вентили (NOT 1/2, NOT, CNOT и др.) осуществляют логические операции над кубитами или парами кубитов.

маленькие квантовые регистры (L<20) могут служить лишь для демонстрации отдельных узлов и принципов работы квантового компьютера, но не принесут большой практической пользы, так как не сумеют обогнать современные ЭВМ, а стоить будут заведомо дороже. В действительности квантовое ускорение обычно значительно меньше, чем приведенная грубая оценка сверху (это связано со сложностью получения большого количества амплитуд и считывания результата), поэтому практически полезный квантовый компьютер должен содержать тысячи кубитов.

Стоит, однако, отметить, что существует класс задач, для которых квантовые алгоритмы не дают значительного ускорения по сравнению с классическими. Одним из первых это показал российский математик Ю. Ожигов, построивший ряд примеров алгоритмов, принципиально не ускоряемых на квантовом компьютере ни на один такт.

И тем не менее нет сомнения, что компьютеры, работающие по законам квантовой механики, - новый и решающий этап в эволюции вычислительных систем. Осталось только их построить.

http://nature.web.ru/db/msg.html?mid=1168929&uri=page3.html

Компьютер на ядерно-магнитном резонансе

первый «опытный образец» — это импульсный ядерный магнитно-резонансный (ЯМР) спектрометр высокого разрешения. Спины ядер, входящих в состав атомов, в свою очередь образующих исследуемую в ЯМР-спектрометре молекулу — это Q-биты, единицы измерения квантовой информации. Каждое ядро имеет свою частоту резонанса в данном магнитном поле. При воздействии импульсом на резонансной частоте одного из ядер оно начинает эволюционировать, остальные же ядра «молчат». Для того чтобы заставить эволюционировать второй атом, надо взять другую частоту и дать импульс на ней. Однако в настоящее время удается работать с системами с общим числом спинов не более пяти-семи.

Компьютер на ионных ловушках

ионные ловушки удалось «растянуть» и получить одномерный ионный кристалл, удерживаемый и в осевом, и в радиальном направлении внешними полями. У каждого иона кристалла берутся два уровня энергии — это один Q-бит; между собой эти ионы связаны через колебания внутри одномерного кристалла, который имеет набор резонансных частот.

Кремний

В нужных местах на расстояниях порядка 100 ангстрем располагают атомы фосфора — обычная примесь в кремнии, которая прекрасно изучена. Если на таком расстоянии расположить два атома фосфора, то облака внешних электронов немного пересекутся, что необходимо для их взаимодействия, и атомы смогут обмениваться состояниями. Один атом управляет электронами другого. Над этими атомами делаются 50-ангстремные электродики, и с помощью напряжения на этом электроде меняют резонансную частоту спина ядра атома фосфора.

http://quantumcomputers.narod.ru/lib/valiev.html

Квантовый Компьютер на электронном спиновом резонансе в структурах Ge–Si

...

Квантовые Вентили(Гейты):

.

.

.

сдвиг фазы

Обозначения этих преобразований являются общепринятыми. I - тождественное преобразование, X - отрицание, Z - операция сдвига по фазе, а Y = ZX - комбинация последних двух.

Преобразование Адамара:

.

to

to

Вентиль CONTROLLED-NOT, или C_not, действует на два кубита следующим образом: второй кубит изменяет свое значение, если первый равен единице, и остаётся без изменений, если первый равен нулю.

Удобно представлять преобразования квантового состояния графически, особенно в случаях, когда проводится несколько преобразований. Вентиль C_not обычно представляют в виде схемы, показанной на рис .

Рис. 5: Вентиль CONTROLLED-NOT

Квантовое программирование

Существующие языки квантового программирования: QPL, QCL, Haskell-подобный QML.

Их цель не столько создание инструмента для программистов, сколько предоставление средств для исследователей для облегчения понимания работы квантовых вычислений.

Библиотеки симуляции квантовых компьютеров (квантовые виртуальные машины, Quantum virtual machine): en:libquantum, qlib.