Вопрос 32. 1.1. Направление выпуклости графика функции.

Определение. Говорят, что график функции y = f (x) имеет на интервале (a,b) выпуклость,

направленную вниз (вверх), если график этой функции лежит не ниже ( не выше) любой своей

касательной.

Теорема. Если функция y = f (x) имеет на интервале (a,b) конечную вторую

производную и если эта производная неотрицательна (неположительна) всюду на этом

интервале, то график функции имеет на интервале (a,b) выпуклость, направленную вниз

(вверх).

1.2. Точки перегиба графика функции.

Определение. Точка M(c, f (c)) графика функции y = f (x) называется точкой перегиба

этого графика, если существует такая окрестность точки x = c оси абсцисс, в пределах

которой график функции справа и слева от точки c имеет разные направления

выпуклости.

1.3. Необходимое условие перегиба графика дважды дифференцируемой функции.

Пусть функция f (x) имеет в точке x = c непрерывную вторую производную. Тогда, если

точка (c, f (c)) является точкой перегиба графика функции, то f ''(c) = 0 .

1.4. Достаточное условие перегиба.

Если функция f (x) дифференцируема в точке x = c , дважды дифференцируема в

некоторой окрестности точки c , за исключением, быть может, самой точки c и вторая

производная f ''(x) меняет знак при переходе аргумента через точку c , то точка (c, f (c))

является точкой перегиба графика функции.

Вопрос 33 Асимптоты графика функции. Определение. Прямая x = a называется вертикальной асимптотой графика функции y = f (x) , если хотя бы одно из предельных значени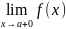й или равно +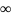 или - .

Определение. Прямая y = kx + b называется наклонной асимптотой графика функции y = f (x) при 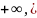x → x →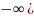 , если f (x) представима в виде f (x) = kx +b 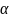+ (x), где (x)

— бесконечно малая функция при 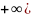x → x → .

Вопрос 34. Общая схема исследования функции и построения ее графика

• Найти область определения функции. Выделить особые точки (точки разрыва).

• Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.

• Найти точки пересечения с осями координат

• Установить, является ли функция чётной или нечётной.

• Определить, является ли функция периодической или нет (только для тригонометрических функций, остальные непериодические, пункт пропускается).

• Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции.

• Найти точки перегиба и интервалы выпуклости-вогнутости.

• Найти наклонные асимптоты функции.

• Построить график функции.