
- •Вопрос 1.
- •Вопрос 2. 1.1. Рациональными называются числа вида m/n, где m z, n n.
- •Вопрос 3. 1.1 Если каждому натуральному числу n ставится в соответствие по
- •Вопрос 4. 1.1. Суммой (разностью) двух последовательностей и называется
- •Вопрос 6. 1.3. Арифметические операции над сходящимися последовательностями приводят к таким же арифметическим операциям над их пределами.
- •Вопрос 7. 1.1. Предельный переход в неравенствах
- •Вопрос 9. 1.1. Понятие функции
- •Вопрос 10. 1.1. Число b называется правым (левым) пределом функции f (X) в точке a ,
- •Вопрос 12. 1.1. Первый замечательный предел. Теорема. Предельное значение функции
- •Вопрос 13. 1.1. Второй замечательный предел
- •Вопрос 14. 1.1. Функция f (X) называется непрерывной в точке a , если предельное
- •Вопрос 15. 1.1. Сложная функция и ее непрерывность. Последовательное применение двух или нескольких функций называется суперпозицией
- •Вопрос 16. 1.1. Функция f (X) называется неубывающей (невозрастающей) на множестве
- •Вопрос 17. 1.1. Элементарными функциями называются функции, полученные в результате суперпозиции
- •Вопрос 20. 1.1. Правила вычисления производных, связанные с арифметическими операциями
- •Вопрос 22. 1.1. Логарифмическая производная.
- •Вопрос 24. 1.1. Главная линейная часть приращения функции a X называется дифференциалом функции
- •Вопрос 25. 1.1. Производные высших порядков([1], глава 5, § 10, п. 1)
- •Вопрос 28. 1.1. Теорема Ролля. Пусть функция f (X) непрерывна на отрезке и дифференцируема во всех
- •Вопрос 29. 1.1. Правило Лопиталя. Правило говорит, что если функции и обладают следующим набором условий:
- •Вопрос 31. 1.1. Для отыскания у дифференцируемой функции точек
- •Вопрос 32. 1.1. Направление выпуклости графика функции.
- •Вопрос 34. Общая схема исследования функции и построения ее графика
Вопрос 29. 1.1. Правило Лопиталя. Правило говорит, что если функции и обладают следующим набором условий:
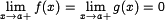 или
или
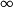 ;
;
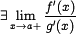 ;
;
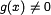 в
некоторой окрестности точки
в
некоторой окрестности точки
 ,
,
тогда существует
![]() .
.
Вопрос 30. 1.1. Функция f (x) возрастает (убывает) в точке x = c , если найдется такая
окрестность точки c , в пределах которой f (x) > f (c) при x > c и f (x) < f (c) при x < c (f (x) < f (c) при x > c и f (x) > f (c) при x < c ).
1.2. Если функция f (x) дифференцируема в точке c и f ‘(c) > 0 (f ‘(c) <0), то эта
функция возрастает (убывает) в точке c .
1.3. Для того, чтобы дифференцируемая на интервале функция f (x) не убывала
(не возрастала) на этом интервале необходимо и достаточно, чтобы производная этой функции
была неотрицательной (неположительной) на этом интервале.
Если всюду на интервале a,b производная функции f (x) положительная (отрицательная),
то функция на этом интервале строго возрастает (строго убывает).
Вопрос 31. 1.1. Для отыскания у дифференцируемой функции точек
возможного экстремума следует найти все корни уравнения f ‘(x) = 0 .
Точки, в которых производная функции f (x) обращается в нуль, называются
стационарными точками.
1.2. Теорема (первое достаточное условие локального экстремума). Пусть точка x = c
является точкой возможного экстремума функции f (x), и пусть функция f (x) дифференцируема
всюду в окрестности точки c . Тогда, если в пределах указанной окрестности производная f ‘(x)
положительна слева от точки c и отрицательна справа от точки c , то функция f (x) имеет в этой
точке локальный максимум. Если же производная f ‘(x) отрицательна слева от точки c и
положительна справа от точки c , то функция f (x) имеет в этой точке локальный минимум. В
случае, когда производная f ‘(x) имеет один и тот же знак слева и справа от точки c , то точка c
не является точкой локального экстремума.
Теорема (второе достаточное условие локального экстремума). Пусть точка x = c
является точкой возможного экстремума функции f (x), и пусть функция f (x) имеет в точке c
конечную вторую производную. Тогда точка c является точкой локального максимума, если
f ‘’(c) < 0 , и минимума, если f ‘’(c) >0.
1.3. Теорема. Пусть функция f (x) дифференцируема всюду в некоторой окрестности точки c ,
за исключением, быть может, самой точки c , и непрерывна в точке c . Тогда, если в пределах
указанной окрестности производная f ‘(x) положительна (отрицательна) слева от точки c и
отрицательна(положительна) справа от точки c , то функция f (x) имеет в этой точке локальный
максимум (минимум).
1.4. Наибольшим (наименьшим) значением функции на множестве называется значение
функции в точке x0 , принадлежащей этому множеству, если для любого x справедливо
неравенство f (x0 ) ≥ f (x) (f (x0 ) ≤ f (x)).
Наибольшее (наименьшее) значение функции называют также глобальным максимумом
(минимумом).
Пусть функция f (x) непрерывна на отрезке . Тогда согласно второй теореме
Вейерштрасса функция достигает на этом отрезке своих точной верхней и нижней граней, то есть
найдутся точки, принадлежащие этому отрезку, в которых функция принимает наибольшее и
наименьшее значение. Причем наибольшее и наименьшее значения функция принимает либо в
точке
локального экстремума, либо в граничной
точке, то есть
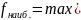
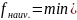
где ci — точки локальных экстремумов на отрезке .
