Вопрос 22. 1.1. Логарифмическая производная.

Пусть функция y = f (x) положительна и дифференцируема в данной точке x . Тогда в этой

точке существует ln y = ln f (x) . Логарифмической производной функции y = f (x)

называется производная от логарифма этой функции, то есть

(ln y)`= y` / y .

1.2. Эластичностью функции y = f (x) называется предел отношения относительного

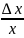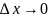приращения функции к относительному приращению переменной при . Из

определения эластичности, обозначаемой Ex ( y) следует, что 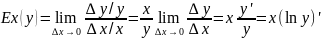, то есть эластичность равна произведению независимой переменной x на логарифмическую

производную функции y = f (x) .

Вопрос 24. 1.1. Главная линейная часть приращения функции a X называется дифференциалом функции

в точке x0 , соответствующим приращению аргумента x , и обозначается символом dy или

df (x0 ) .

1.2.

1.3.

Вопрос 25. 1.1. Производные высших порядков([1], глава 5, § 10, п. 1)

Пусть функция y = f (x) определена и дифференцируема на интервале (a,b). Тогда ее

производная f ‘(x) представляет собой функцию переменной x также определенную на интервале

(a,b) . f '(x) в свою очередь может оказаться дифференцируемой в некоторой точке x интервала (a,b).

Производную от функции f ' (x) называют второй производной (производной второго порядка) от

функции f (x) и обозначают f ''(x) или y'' . Итак, y''= f ''(x) = (f '(x))' .

Вопрос 26. 1.1. Дифференцирование функции, заданной параметрически. Пусть x и y заданы как функции некоторого параметра t : x = (t), y = (t).

Предположим, что эти функции дифференцируемы в некоторой области изменения переменной t ,

а функция x = (t) имеет в указанной области обратную функцию t = (x) . Тогда функцию y

можно рассматривать как сложную функцию переменной x . Найдем производную функции y по

переменной x . В силу инвариантности формы первого дифференциала имеем .

Вопрос 27. 1.1. Точка x = c называется точкой локального максимума, если найдется 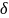-окрестность точки c , в пределах которой значение f (c) является наибольшим, то есть для любого x из интервала  справедливо неравенство f (c) ≥ f (x).

Точка x = c называется точкой локального минимума, если найдется - окрестность точки c , в пределах которой значение f (c) является наименьшим, то есть для

любого x из интервала  справедливо неравенство f (c) ≤ f (x).

1.2. Локальный максимум и локальный минимум объединяются общим названием локальный

экстремум.

1.3. Теорема Ферма (необходимое условие локального экстремума дифференцируемой

функции). Если функция f (x) дифференцируема в точке c и имеет в этой точке локальный

экстремум, то f ‘(c) = 0.

Вопрос 28. 1.1. Теорема Ролля. Пусть функция f (X) непрерывна на отрезке и дифференцируема во всех

внутренних точках этого отрезка. Пусть, кроме того, f (a) = f (b). Тогда внутри отрезка

найдется точка 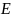такая, что значение производной в этой точке f ‘( ) равно нулю.

1.2. Теорема Лагранжа. Если функция f (x) непрерывна на отрезке и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка найдется точка такая, что справедлива формула f (b) - f (a) = f ‘( )(b- a) .

1.3. Теорема Коши. Если каждая из функций f (x) и g(x) непрерывна на отрезке и

дифференцируема во всех внутренних точках этого отрезка и если, кроме того, производная

g’(x) отлична от нуля всюду внутри отрезка , то внутри отрезка найдется точка

такая, что справедлива формула