Вопрос 15. 1.1. Сложная функция и ее непрерывность. Последовательное применение двух или нескольких функций называется суперпозицией

этих функций.

Функции, образованные в результате суперпозиции двух или нескольких функций будем

называть сложными функциями. Например, сложная функция sin(ln x) образована в результате

суперпозиции функций sin u и u = ln x .

Достаточно определить сложную функцию, образованную в результате суперпозиции двух

функций. Пусть функция x = (t) определена на некотором множестве и пусть —

множество значений этой функции. Если на указанном множестве определена другая функция

y = f (x) , то говорят, что на множестве задана сложная функция переменной t

y = f (x) = f ( (t)) = F(t) .

Теорема. Если функция x = (t) непрерывна в точке t = a , а функция y = f (x) непрерывна

в точке x = b = (a), соответствующей точке t = a , то функция F(t) непрерывна в точке a .

Вопрос 16. 1.1. Функция f (X) называется неубывающей (невозрастающей) на множестве

, если для любых x1 и x2 из этого множества, удовлетворяющих условию x1 < x2 , справедливо

неравенство f (x1 ) ≤ f (x2) (f (x1 ) ≥ f (x2)). Неубывающие и невозрастающие функции

называются монотонными.

1.2. Функция x = ( y) называется обратной для функции y = f (x).

1.3.

Вопрос 17. 1.1. Элементарными функциями называются функции, полученные в результате суперпозиции

простейших элементарных функций и арифметических действий.

Все основные элементарные функции непрерывны при всех значениях х, для которых они определены.

Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Вопрос 18. 1.1. Производная 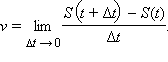Производная функции равняется пределу отношения приращения функции к приращению аргумента, когда приращения аргумента стремится к 0.

1.2. Физический смысл производной. Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.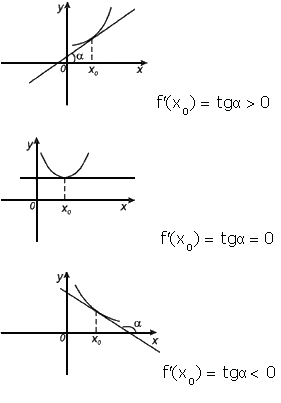

1.3. Использование понятия производной в экономике

Рассмотрим издержки производства y как функцию количества выпускаемой продукции x . Пусть x — прирост продукции, а y — приращение издержек производства. Тогда отношение — это средние издержки производства на одну единицу продукции. Производная называется предельными издержками производства. Аналогично можно определить