Вопрос 9. 1.1. Понятие функции

Если каждому значению переменной x из некоторого множества 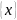ставится в

соответствие по известному закону единственное число y , то говорят, что на множестве x

задана функция y = y(x) или y = f (x).

1.2. Различают 4 способа задания функции:

1. табличный Состоит в простом перечислении элементов функции f, т.е. при этом способе указывается значение аргумента x и соответствующе значение функции y=f(x)

2. аналитический (формулы) Одна и та же функция может быть задана различными формулами: y=∣sin(x)∣y=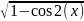

3. графический Область определения -- проекция данного графика на Ох, а множество значений -- проекция Д(f) на Оу.

1.3 Предел функции f(x) в точке a существует тогда и только тогда, если для каждого ε > 0  найдется δ = δ(ε) > 0 такое, что |f(x’) – f(x’’)| < ε.

Вопрос 10. 1.1. Число b называется правым (левым) пределом функции f (X) в точке a ,

если для любой сходящейся к a последовательности значений аргумента функции, все

элементы которой больше (меньше) a , соответствующая последовательность 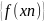значений

функции сходится к b . Такие пределы называются односторонними пределами.

1.2. Число b называется пределом функции f (x) при x → ∞ , если для любой

бесконечно большой последовательности значений аргумента функции соответствующая

последовательность значений функции сходится к b . Число b называется пределом функции f (x) при x → +∞ ( x → -∞ ), если для

любой бесконечно большой последовательности значений аргумента функции, элементы

которой, начиная с некоторого номера, положительны (отрицательны), соответствующая

последовательность значений функции сходится к b .

Вопрос 11. 1.1. Функция f (x) называется бесконечно малой в точке x = a (при x → ∞),

если ее предельное значение в этой точке (при x → ∞) равно нулю.

1.2. Функция f (x) называется бесконечно большой при x → +∞ ( x → -∞ ), если для любой бесконечно большой последовательности {xn} значений аргумента x ,

все элементы которой положительны (отрицательны), соответствующая последовательность

значений функции { f (xn)} является бесконечно большой последовательностью определенного

знака.

Вопрос 12. 1.1. Первый замечательный предел. Теорема. Предельное значение функции

в точке x = 0 существует и равно единице: 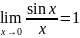(1)

Равенство (1) называют первым замечательным пределом.

Вопрос 13. 1.1. Второй замечательный предел

Теорема. Предельное значение функции 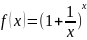при x →∞ существует и равно e :

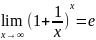
Второй замечательный предел также записывают в виде: .

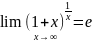Вопрос 14. 1.1. Функция f (X) называется непрерывной в точке a , если предельное

значение этой функции в точке a существует и равно частному значению f (a), то есть, если

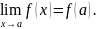
1.2. Функция называется непрерывной на множестве , если она непрерывна

в каждой точке этого множества.

1.3. Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке.

1.4. Разрыв первого рода. Точка a называется точкой разрыва первого рода, если в этой точке

функция f (x) имеет конечные, но не равные друг другу правое и левое предельные значения: .

Например, для функции f(x) = 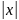/ x точка x =0 является точкой разрыва первого рода.

Действительно, 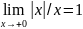, а

Разрыв второго рода. Точка a называется точкой разрыва второго рода, если в этой точке

функция f (x) не имеет хотя бы одного одностороннего предельного значения, или если, по

крайней мере, одно из односторонних предельных значений бесконечно.

Ранее мы показали, что функция 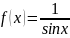не имеет предельного значения в точке x = 0 .

Следовательно, точка x = 0 является для данной функции точкой разрыва второго рода.

Функция f (x) = tg x также имеет в точке x =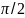 разрыв второго рода, поскольку