Вопрос 1.

1.1. Под множеством понимается совокупность элементов (объектов) той или иной природы.

Множества обычно обозначают большими буквами латинского или другого алфавита:

A, B, X, а элементы множества малыми буквами a, b, x,…

Под отображением множества X в Y будем понимать следующее: каждому элементу X соответствует единственный элемент из Y. Элемент y - образ элемента x, если он соответствует  отображению и обозначается y=f(x); x прообраз y.

1.2. Множество A называется подмножеством множества B , если каждый элемент множества

A принадлежит множеству B . В этом случае пишут A B . Последнюю запись можно прочитать

и так: множество A заключено (содержится) в множестве B .

1.3. Множества A и B называются равными, если они состоят из одних и тех же элементов , то

есть равенство A = B означает, что одно и тоже множество обозначено разными буквами.

1.4. Операции над множествами

Пусть A и B — произвольные множества.

Объединением или суммой множеств A и B называется множество C , состоящее из всех

элементов, принадлежащих хотя бы одному из множеств A и B . Объединение множеств A и B

обозначается символом A 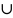B .

Пересечением множеств A и B называется множество C , состоящее из всех элементов,

принадлежащих как множеству A, так и множеству B , Пересечение множеств A и B

обозначается через A 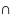B .

Разностью множеств A и B называется множество C , состоящее из элементов,

принадлежащих множеству A, но не принадлежащих множеству B , то есть

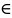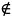C =A \ B = {c | c A и с B}.

Если B A, то разность A\B называется дополнением множества B до множества A и

обозначается 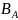= {c | c A, c B, B A} .

1.5. Отображение из A в B называется взаимно-однозначным, если

1) разные элементы из A имеют разные образы

2) каждый элемент из B является образом некоторого элемента из A.

1.6. Множества, между которыми установлено взаимно однозначное соответствие, называются

эквивалентными.

1.7. Множества, эквивалентные множеству натуральных чисел, называются счетными.

Например, множество целых чисел счетно.

1.8. Множество называется конечным, если его элементы можно поставить в соответствие

числа из конечного натурального ряда {1, 2, ... , n}, где n — конечное число. Множества, не

являющиеся конечными принято называть бесконечными. Например, множества натуральных и

целых чисел бесконечны.

1.9. Множество вещественных чисел X называется ограниченным сверху

(снизу), если найдется такое вещественное число M (m) , что для каждого элемента x множества

X справедливо неравенство x ≤ M ( x ≥ m). При этом число M называют верхней гранью

множества X , а число m — нижней гранью множества X .

Множество вещественных чисел X называется неограниченным сверху

(снизу), если для любого вещественного числа M (m) найдется элемент x множества X ,

удовлетворяющий неравенству x > M ( x < m ).

Вопрос 2. 1.1. Рациональными называются числа вида m/n, где m z, n n.

Иррациональным числом называется всякая бесконечная непериодическая десятичная дробь.

Все рациональные и иррациональные числа образуют множество

вещественных (действительных) чисел. Множество вещественных чисел обозначают R .

1.2. Сравнение вещественных чисел. Рассмотрим два произвольных вещественных числа:

a = a0 , a1a2 ...an ... (1)

b = b0 ,b1b2 ...bn ... (2)

Здесь из двух знаков  берется какой-то один.

Два вещественных числа называются равными, если они имеют одинаковые знаки и

справедливы равенства

a0 = b0 , a1 = b1 , a2 = b2 , …, an = bn , …, (3)

то есть a0 = b0 , ai = bi , i N .

Пусть даны два неравных неотрицательных вещественных числа a = a0 , a1a2 ...an... и

b = b0 ,b1b2 ...bn ... . Установим правило, при помощи которого можно прийти к заключению, какое

из двух чисел больше. Так как a b , то нарушается одно из равенств (3). Обозначим через k

наименьший из номеров, для которых равенства (3) не справедливы. Пусть

a0 = b0 , a1 = b1 , a2 = b2 , …, ak 1 = bk 1 , ak = bk .

Тогда, если ak bk , то a b , а если ak bk , то a b .

Если одно из двух чисел отрицательно, а другое неотрицательно, то будем считать, что

неотрицательное число больше отрицательного.

Прежде, чем рассматривать правило сравнения отрицательных чисел, введем понятие

модуля вещественного числа. Модулем вещественного числа a называется неотрицательное

число, обозначаемое a и равное десятичной дроби, представляющей число a , взятой со знаком

плюс (+).

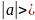Если числа a и b оба отрицательные, то a b , если b , и a < b , если b

Правило сравнения вещественных чисел обладает следующим свойством: если a > b и

b > c , то a > c .

1.3. Арифметические операции с вещественными числами.

1. При сложении и вычитании сначала уравниваются порядки слагаемых. В результате одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются

2. Вычитание сводится к сложению с дополнительным кодом.

3. Умножение производится по правилу - мантиссы перемножаются, а порядки складываются. Если нужно, то полученное число нормализуется.

4. Деление производится по правилу - мантиссы делятся (делимое на делитель), а порядки вычитаются (порядок делителя из порядка делимого). Если нужно, то полученное число нормализуется.

1.4. Свойства вещественных чисел

Любое вещественное число можно с заданной точностью с двух сторон приблизить рациональными числами.

Между любыми двумя несовпадающими вещественными числами содержится целое бесконечное множество рациональных. Кроме того, ещё более очевидно, что между любыми двумя различными рациональными числами содержится вещественное