2.2.3. Комплексная мощность

Комплексная мощность есть произведение комплексного напряжения на сопряженный комплексный ток цепи:

.

Это показательная форма записи комплексной мощности. Здесь S – полная мощность цепи;   угол сдвига фаз между напряжением и током;  комплексный ток, сопряженный заданному комплексному току . Переходя от показательной к алгебраической форме записи, находим, что ее вещественная часть Scos соответствует активной мощности цепи Р, а ее мнимая часть Ssin  реактивной мощности цепи Q. Поэтому

. (2.25)

2.3. Резонансные явления

Резонансом в цепи, содержащей сопротивления индуктивности и емкости, называется такой режим, при котором ток и напряжение на входе цепи совпадают по фазе

Существуют резонанс напряжений и резонанс токов.

Резонанс напряжений.

Комплексное сопротивление цепи, состоящей из последовательно соединенных элементов R, L и C, имеет вид

.

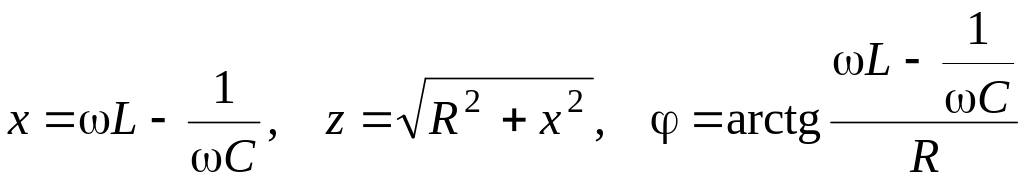Резонанс имеет место, как указано выше, при φ = 0, что равносильно при последовательном соединении условию

т. е. .

Резонанса можно достичь, изменяя или частоту приложенного к цепи напряжения, или индуктивности катушки, или емкости конденсатора.

Условием резонанса при параллельном соединении активного, индуктивного и емкостного сопротивлений является также отсутствие сдвига фаз между током и напряжением на входе цепи.

2.4. Индуктивно связанные цепи

Если при изменении во времени тока в одной катушке на зажимах второй возникает ЭДC, такие катушки называются индуктивно связанными. При протекании в первой катушке синусоидального тока в ней возникает магнитное поле, характеризуемое потокосцеплением самоиндукции , где – число витков первой катушки; Ф – магнитный поток, проходящий через один виток катушки. Это потокосцепление в соответствии с законом электромагнитной индукции индуцирует в первой катушке ЭДС самоиндукции:

е_L1 .

Напряжение на этой катушке численно равно этой ЭДС, но направлено в противоположную сторону и поэтому имеет обратный знак:

=  = + =L ,

где = ,  индуктивность первой катушки.

В комплексной форме записи это напряжение имеет вид , где  индуктивное сопротивление первой катушки.

При наличии магнитной связи между катушками 1 и 2 некоторая часть потокосцепления самоиндукции первой катушки проникает во вторую катушку. Эта его часть называется потокосцеплением взаимной индукции второй катушки, вызванным током первой катушки.

Потокосцепление индуцирует во второй катушке ЭДС взаимной индукции: . Отношение потокосцепления взаимной индукции к току в первой катушке есть взаимная индуктивность этих катушек: . Взаимная индуктивность так же, как и собственная индуктивность, измеряется в генри (Гн). С учетом последнего соотношение ЭДС взаимной индукции второй катушки приобретает вид:

.

Аналогичные рассуждения можно привести и для случая, когда синусоидальный ток протекает только по 2-й катушке (рис. 2.16, б). Потокосцепление самоиндукции второй катушки индуцирует в ней электродвижущую силу самоиндукции . Напряжение на второй катушке равно ей по величине и противоположно по знаку: . Здесь , где  индуктивность 2-й катушки. В символической форме записи это напряжение имеет вид , где  индуктивное сопротивление 2-й катушки.

Некоторая часть потокосцепления самоиндукции проникает в первую катушку и образует там потокосцепление взаимной индукции . Оно индуцирует в 1-й катушке ЭДС взаимной индукции . Отношение потокосцепления взаимной индукции к току во второй катушке есть взаимная индуктивность этих двух катушек: = М₁₂. С учетом этого соотношения ЭДС взаимной индуктивности в первой катушке .