2.2. Комплексный метод расчета электрических цепей

2.2.1. Комплексные токи и напряжения

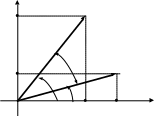
Положения векторов токов и напряжений на комплексной плоскости показаны на рис. 2.5. Здесь  комплексное действующее значение напряжения (сокращенно – комплексное напряжение);  комплексное действующее значение тока (сокращенно – комплексный ток).

Аналитическая запись и имеет вид

. (2.20)

+j

b₁



b₂ _u

_i +1

0 a₁ a₂

Рис. 2.5

Формулы (2.20) представляют собой алгебраическую, тригонометрическую и показательную формы записи.

2.2.2. Комплексное сопротивление и комплексная проводимость

а) Комплексное сопротивление Z есть отношение комплексного напряжения к комплексному току :

.

Это показательная форма записи. Здесь z – полное сопротивление цепи, а   угол сдвига фаз между напряжением и током.

Переходя к алгебраической форме записи Z через тригонометрическую, находим, что его вещественная часть zcos соответствует активному сопротивлению цепи R, а его мнимая часть zsin соответствует реактивному сопротивлению Х. Поэтому

. (2.21)

б) Комплексная проводимость Y есть величина, обратная комплексному сопротивлению Z и равная отношению комплексного тока к комплексному напряжению:

.

Это показательная форма записи. Здесь y – полная проводимость цепи, а   угол сдвига фаз между напряжением и током.

Аналогично находим, что ее вещественная часть ycos соответствует активной проводимости цепи G, а ее мнимая часть y sin  реактивной проводимости b. Поэтому

. (2.22)

Таким образом, комплексная проводимость содержит в себе полную проводимость у, активную проводимость G, реактивную проводимость b и угол сдвига фаз  между напряжением и током.

Комплексные формы записи чисто активных, чисто индуктивных и чисто емкостных сопротивлений имеют вид

; ; .

Законы Кирхгофа в комплексной форме записи и алгоритмы составления уравнений по этим законам выполняются.

Первый закон Кирхгофа: алгебраическая сумма комплексных токов в узле равна нулю:

. (2.23)

Второй закон Кирхгофа:

. (2.24)