1.2.4. Применение законов Кирхгофа для расчетов сложных цепей
Сложными называются разветвленные электрические цепи со многими источниками энергии и приемниками.
Для ее расчетов, т. е. для определения токов во всех ее ветвях, необходимо составить систему уравнений по законам Кирхгофа. Общее число уравнений в системе должно соответствовать числу неизвестных нашей цепи, это пять неизвестных токов. При этом
а) по первому закону Кирхгофа составляется число уравнений на единицу меньшее числа узлов цепи, поскольку уравнение для последнего узла есть следствие всех предыдущих уравнений и не дает ничего нового для расчета.
б) по второму закону Кирхгофа составляются все недостающие уравнения для любых произвольно выбранных контуров цепи.
Предварительно следует задаться (произвольно) направлением токов во всех ветвях цепи и направлением обхода выбранных контуров. При составлении уравнений по 1-му закону Кирхгофа в соответствии с формулой (1.5) токи, подходящие к узлу, будем считать положительными и брать со знаком (+), а токи, отходящие от узла, – отрицательными и брать со знаком (). При составлении уравнений по второму закону Кирхгофа в соответствии с формулой (1.6) ЭДС и токи, совпадающие с выбранным направлением обхода контура будем брать со знаком (+), а несовпадающие – со знаком ().
Вопросы для самопроверки
1. Дайте определения ветви, узлу и контуру.
2. Сформулируйте первый закон Кирхгофа.
3. Сформулируйте второй закон Кирхгофа.
4. Напишите уравнения элементов R, L и C.
5. Чему равны сопротивления элементов L и C при постоянном токе?
6. Как соотносятся между собой электроэнергия и мощность в цепи постоянного тока?
7. Сколько уравнений надо составить по первому закону Кирхгофа при расчете сложной цепи?
8. Сколько уравнений надо составить по второму закону Кирхгофа при расчете сложной цепи?
9. Напишите уравнение баланса мощностей для сколько угодно сложной цепи постоянного тока.
Раздел 2. Линейные цепи синусоидального тока
2.1. Основные понятия о синусоидальных процессах
2.1.1. Способы графического изображения синусоидальных токов и напряжений
Синусоидальный
ток
– это периодический ток, изменяющийся
во времени по закону синуса
График
этого тока представлен на рис. 2.1 в виде
кривой, полученной на экране осциллографа.
Максимальное значение тока (относительно оси t) называется амплитудой и обозначается Im . Синусоидальный ток изменяется во времени от +Im до –Im.
Наименьшее время Т, по истечении которого значения тока повторяются, называется периодом тока. Число периодов, совершаемых током за одну секунду, называется частотой тока f . Частота тока и период тока – величины взаимообратные. Частота f измеряется в герцах (Гц):
.
(2.1)
Экран осциллографа
Т
Ось тока
Ось времени
При теоретических расчетах часто используют понятие об угловой (круговой) частоте. Угловая частота связана с частотой f соотношением
(2.2)
и измеряется в рад/ с.
Все сказанное выше о синусоидальном токе справедливо и по отношению к синусоидальному напряжению и синусоидальной ЭДС.
Существует способ графического изображения синусоидальных токов и напряжений с помощью вращающихся векторов в полярных координатах.
На рис. 2.2, а
показано изображение тока в виде
вектора длиной Im,
вращающегося (как принято в теории
цепей) против часовой стрелки с
постоянной угловой скоростью
относительно полюса 0 полярной системы
координат. Его положение на этом рисунке
зафиксировано в момент времени t
= 0, при котором угол его наклона к
полярной оси Р составляет величину,
равную начальной фазе +
(положительные начальные фазы откладывают
от полярной оси против часовой стрелки,
а отрицательные – по часовой).
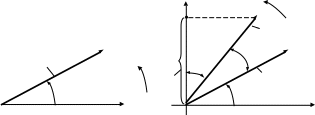а)
б)
при t
> 0
t
= 0
= t
I m +
i при t = 0
0 P 0 P
Рис. 2.2
Совокупность векторов токов и напряжений цепи, называется векторной диаграммой этой цепи.
В электроэнергетике большое значение придается углу сдвига фаз между напряжением и током цепи. Он определяется как разность начальных фаз напряжения и тока (с учетом их собственных знаков) и обозначается греческой буквой :
= u – i . (2.3)