4. Формирование обучающей и проверочной последовательностей

Как было упомянуто ранее исходную выборку следует разбивать на две подвыборки A и B. Подвыборка A используется для определения коэффициентов модели (обучающая последовательность), а подвыборка B — для определения качества (проверочная последовательность). При этом соотношение количества данных в обеих выборках может быть как 50/50, так и 60/40.

Рассмотрим задачу отыскания правила разбиения всего множества имеющихся изображений (исходного множества) на два подмножества (обучающую и проверочную последовательности) в зависимости от свойств исходного множества.

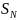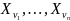Пусть — основное выборочное пространство объектов, причем каждому объекту из соответствует одно из вполне определенных изображений . Предположим, что некоторая перестановка изображений из 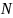(n<N). Будем говорить о подмножестве 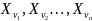как о 1-й выборке объема из конечной совокупности . Каждая составляющая этой совокупности может быть многомерным вектором в пространстве признаков. Предполагается, что распределение совокупности остается неизменным в течение всего наблюдения.

Для того чтобы определить статистические свойства конечной совокупности по выборке объема , нужно найти такое , чтобы результаты статистической обработки любой выборки объема хорошо согласовались с результатами обработки всей совокупности. Кроме того, нужно, чтобы оставшееся подмножество из ( ) элементов достаточно хорошо характеризовало конечную совокупность .

(*) Предположим, что задача состоит в оценке каких-либо параметров. Допустим, что оценивается некоторый параметр 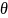по выборке объема , например какой-либо коэффициент уравнения. Обозначим через 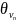оценку параметра по 1-й выборке объема . Тогда согласно неравенству Чебышева имеем

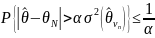, (1.7)

где — математическое ожидание оценок 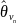; 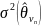— дисперсия оценок . Очевидно, что является функцией по крайней мере двух переменных: и . При 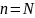эта функция обращается в нуль, а по мере возрастания разности также возрастает. Обозначим ее следующим образом: .

В неравенстве (1.7) величина 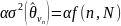определяет порог, который с вероятностью, не большей, чем , не будет превышен отклонением оценки параметра от его среднего значения, определенного по всем возможным выборкам объемом . Назовем этот порог порогом достоверности выборки объемом .

Для того чтобы оценки, полученные по обучающей и проверочной последовательностям, были одинаково точны, необходимо и достаточно, чтобы пороги достоверности этих выборок были равны, т. е. 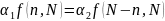, (1.8)

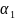где и характеризуют требования, предъявляемые к обучению и проверке соответственно.

При выполнении условия (1.8) пороги достоверности одинаковы и для обучения и для проверки, но вероятности их превышения различны и зависят от выбора и . В любом случае нужно так выбрать , чтобы удовлетворялось равенство (1.8). Так, например, при 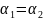это равенство справедливо при 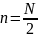для любых функций. Если же 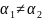, то для определения нужно знать характер функции , что не всегда возможно. Это затрудняет общее решение задачи. Но в конкретных случаях, когда вид функции известен, задача решается полностью. Например, если оцениваемым параметром является математическое ожидание, то

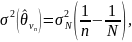
где 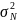— дисперсия, определенная по всей выборке . В этом случае должно выполняться равенство

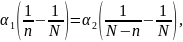
откуда

. (1.9)

Задавая требуемые значения и , можно определить нужный объем обучающей выборки.

Возникает вопрос, нельзя ли, основываясь на статистических свойствах исходного множества, получить какие-либо рекомендации по выбору и . Рассмотрим один из возможных подходов к выбору коэффициентов и . В задаче обучения распознаванию образов. Для простоты будем считать, что основная совокупность состоит из элементов только двух классов: и , причем и 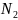— числа элементов, принадлежащих классам и соответственно.

Предлагаемый подход основан на следующем предположении. Если при оценки математического ожидания достаточно точны, то требования к обучению могут быть несколько снижены, а требования к проверке ставятся в прямую зависимость от степени пересечения подмножеств. Если же подмножества таковы, что оценки их математических ожиданий при сильно отличаются от действительных значений, а пересечение этих подмножеств незначительно, то для удовлетворительной классификации следует увеличить точность оценок увеличением объема обучающей последовательности. При этом приходится жертвовать точностью проверки в надежде на то, что при правильной оценке параметров классификация будет удовлетворительной. Если же пересечение подмножеств велико, то никаким повышением точности оценок нельзя избежать ошибочной классификации. Следовательно, в этом случае целесообразно повысить требования к проверке в ущерб обучению путем увеличения объема проверочной последовательности.

Опираясь на это предположение, ориентировочный выбор коэффициентов и для каждого класса в отдельности целесообразно осуществлять согласно формуле

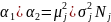, (1.10)

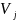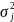где — номер класса ( ); — число изображений класса в совокупности ; — дисперсия класса , определенная по совокупности ; выбирается из соотношения ( — дисперсия классов и соответственно; 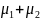— расстояние между средними значениями классов). Задавшись определенным значением по формуле (1.9), можно выбрать соответствующее , которое будет зависеть от статистических свойств . Если классов больше двух, то можно определить для каждой пары классов. Поскольку каждой паре классов соответствует свое соотношение (1.10), то нужно выбирать различным для каждой пары, а из всех , относящихся к одному и тому же классу, нужно выбирать наибольшее. Когда уже определены и для каждого класса, нетрудно по формуле (1.9) определить соответствующие числа . 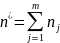Обучающая последовательность составляется из элементов, где — число классов.