В качестве примеров рекомендуется ознакомиться со статьями в приложении или воспользоваться собственными примерами

3. +Коды Хемминга. Матричная запись кода. Покажите на примере кода (7,4)

1. Код, содержащий кодовых слов в разрешенном наборе, может быть задан k линейно-независимыми векторами составляющими базисную матрицу L размером

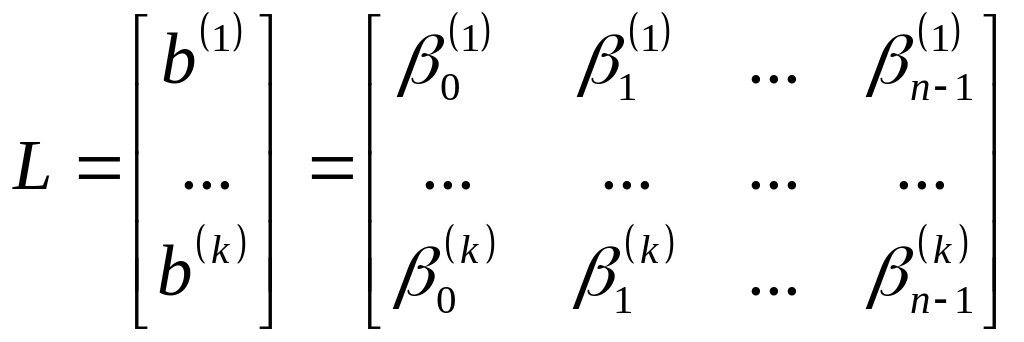` (9.17)

Множество разрешенных кодовых слов, определяемое базисной матрицей L, обозначим B^L. Любое кодовое слово из разрешенного набора B^L, определяемого матрицей (9.17), может быть представлено в виде линейной композиции входящих в нее векторов:

. (9.18)

Нетрудно видеть, что общее число разрешенных кодовых слов, образуемых по закону (9.18), равно числу различных комбинаций из k коэффициентов принимающих одно из значений 0,1, ... m - 1 т.е. закон (9.18) обеспечивает образование заданного числа M = m^k различных кодовых слов длиной п. Таким образом, базисная матрица размером задает линейный код (n, k).

Простой код является линейным кодом (n, n), базисная матрица которого включает полный набор n-мерных линейно-независимых векторов (число линейно-независимых векторов в n-мерном пространстве не может превосходить п).

2. Множеству разрешенных кодовых слов , определяемому матрицей L, отвечает некоторое множество кодовых слов, ортогональных кодовым словам разрешенного набора: если , а , то . Множество может быть задано п - k линейно-независимыми векторами, составляющими матрицу Н размером :

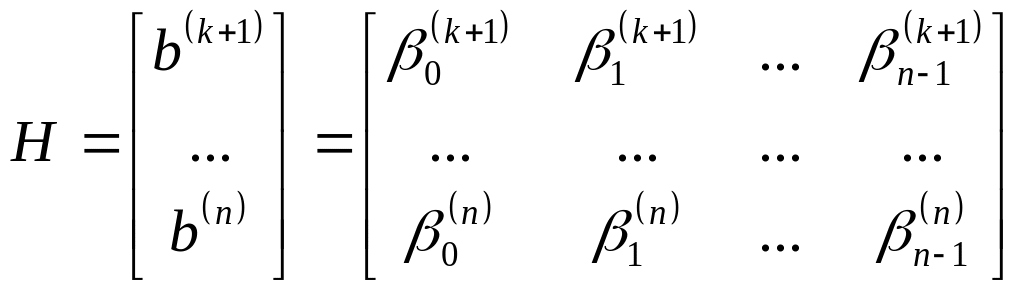
Матрица H называется проверочной. Множество содержит кодовых слов, отвечающих всем возможным линейным композициям векторов, составляющих матрицу H. Свойства множеств и взаимны: множество также представляет линейный код, для которого матрица H является базисной, а матрица L — проверочной.

Проверочная матрица H так же, как и базисная матрица L, полностью определяет линейный код. Она позволяет представить линейный код (n, k) в систематической форме:

(9.19)

где первые k символов — информационные, а последние n-k символов — избыточные, обеспечивающие возможность обнаружения и исправления ошибок (их называют проверочными символами).

Проверочные символы разрешенного кодового слова при заданных информационных символах могут быть определены из n-k линейных уравнений, определяемых условиями ортогональности разрешенного кодового слова кодовым словам проверочной матрицы H:

. (9.20)

Уравнения (9.20) можно переписать в виде:

, (9.21)

Разрешая систему n-k уравнений (9.21) относительно n-k проверочных символов , получим для них линейные выражения вида

, . (9.22)

Формула (9.22) позволяет определить n-k проверочных символов , разрешенного кодового слова по известным k информационным символам (коэффициенты , определяющие закон формирования проверочных символов, выражаются через элементы проверочной матрицы H).

Формула (9.22) является весьма удобной формой задания регулярного линейного кода (n, k), широко используемой в практике связи. При этом для образования разрешенных кодовых слов по известным информационным символам достаточно хранить в памяти значений коэффициентов , водящих в (9.22). Поскольку при задании кода с основанием m для каждого из этих коэффициентов может быть выбрано одно из т значений, то всегда можно выбрать вариантов коэффициентов в (9.22) и построить различных линейный кодов (n, k). Задача заключается в том, чтобы выбрать оптимальный вариант кода