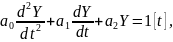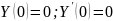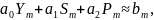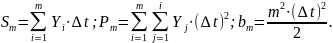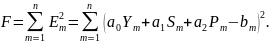Звено второго порядка (колебательное звено)

Такие звенья описываются дифференциальным уравнением вида: , где U – входные воздействия.

Если ввести обозначения 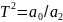; ; 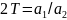; то уравнение примет вид

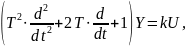
в записи которого содержатся три параметра:

T – постоянная времени (в секундах);

– коэффициент затухания (безразмерная величина);

k – передаточный коэффициент.

Если входное воздействие U=0, то можно получить так называемое характеристическое уравнение

,

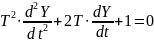касающееся только внутренних свойств звена.

В зависимости от величины звенья второго порядка классифицируются по видам:

= 0 – консервативное звено второго порядка (рис. 8а);

0 < < 1 – колебательное звено второго порядка (рис. 8б);

≥ 1 – апериодическое звено второго порядка (рис. 8в).

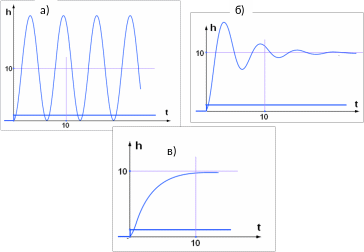
Рис. 8. Переходные характеристики h(t) звеньев 2-го порядка в зависимости от параметра : а) = 0;

б) = 0,2;

в) = 1,5.

Динамические регрессионные модели

Допустим, что на вход системы подана сигнал в виде функции Хэвисайда, а примерный вид динамического сигнала представлен на рис. 9а. Ограничиваясь временем рассмотрения сигнала, равным T, проведена дискретизация сигнала (рис. 9б) – разбиение отрезка [0;T] на n равных промежутков.

а)

б)

Рис. 9. Возможный вид зависимости выходного сигнала от времени а) до дискретизации; б) после дискретизации

Пусть на вход системы подается единичная функция Хэвисайда 1[t], а выходной сигнал описывается уравнением¹

	(6)
с начальными условиями	(7)

Проинтегрируем уравнение (6) дважды от 0 до некоторого произвольного t, учитывая условия (7). После первого интегрирования получим:

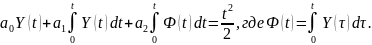
Переходя к численному интегрированию методом правых прямоугольников, получим для любого m = 1,2,...,n:

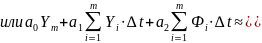
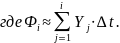
Следовательно, для каждого m = 1,2,...,n (n – число экспериментальных точек) приблизительно верно:

(8)

если использовать обозначения

(9)

Ошибку 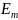, которая показывает, насколько отходит теоретическое значение 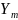от экспериментального в некоторой m-ой точке, можно записать как

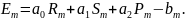
Сумма квадратов ошибок, вносимых всеми точками, которую надо минимизировать, будет:

(10)

Чтобы найти минимум функции F, доставляемый за счет параметров a₀, a₁, a₂, надо взять частные производные F по каждому из параметров и приравнять каждую производную к нулю. В результате получаем систему линейных уравнений:

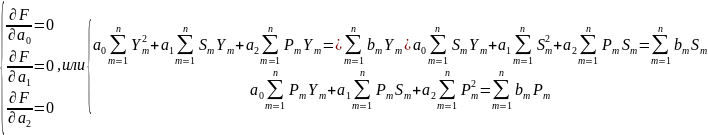
Запишем систему в матричном виде, и решим ее методом Крамера. Можно считать, что задача нахождения коэффициентов модели решена, а система описывается уравнением (6) с начальными условиями (7) и определенными постоянными коэффициентами

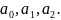
Теперь необходимо сравнить получаемое из этой модели решение Y теоретическое с Y, заданным экспериментально, и вычислить ошибку F. Далее проверить ее значение по критерию – допустимо ли значение вычисленной ошибки, или гипотезу о виде модели требуется сменить на более точную.

Y теоретическое можно получить, аналитически решая дифференциальное уравнение (6)¹.

Считая что коэффициенты модели теперь известны, построим реализацию, имитирующую поведение системы.

Для этого воспользуемся уже полученной ранее формулой (8) с учетом введенных обозначений (9). Поскольку

из выражения

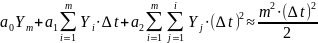
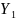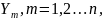можно выразить сначала , а потом тем самым сымитировав поведение системы.