Линейная множественная регрессионная модель

П редположим, что функциональная структура ящика снова имеет линейную зависимость, но количество входных сигналов – m.

Тогда

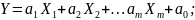
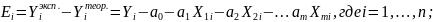
Для нахождения экстремума получим систему из m+1 уравнения:

Такие системы имеет смысл решать методом Крамера, поэтому запишем её в матричном виде:

Вычисляем коэффициенты:

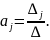
Далее, по аналогии с одномерной моделью, для каждой точки вычисляется ошибка E_i; затем находится суммарная ошибка F и значения σ и S с целью определить, принимается ли выдвинутая гипотеза.

Нелинейные регрессионные модели

В некоторых случаях нелинейные зависимости можно представить в виде линейных путём введения дополнительных коэффициентов. Рассмотрим несколько вариантов.

1 . Ящик имеет 2 входа, а зависимость Y от X₁ и X₂ напоминает квадратичную. Имеет смысл рассмотреть такую гипотезу:

Если обозначить

и считать дополнитель­ными входами, то получим линей­ную множественную регрессион­ную модель.

2 . Если зависимость имеет экспоненциальный вид, т.е. рас­сматривается гипотеза

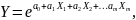
то прологарифмировав левую и правую части уравнения и обозначив , получим

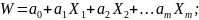
т.е. линейную множественную модель.

3. В случае обратной зависимости:

можно обозначить

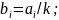
и снова перейти к линейной множественной модели

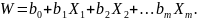
Динамические модели Динамические системы

Д инамические системы, в отличие от статических, помнят свое прошлое состояние, то есть обладают памятью. Следовательно, существуют зависимости входного и выходного сигналов от времени: X=X(t) и Y=Y(t), причем эти зависимости могут быть самыми разными.

В записи модели динамических систем присутствует производная, связывающая прошлое состояние системы с настоящим. Чем большей памятью обладает система, тем больше состояний из прошлого влияют на настоящее, тем большая степень старшей производной используется в записи модели, и тем больше параметров надо определить, чтобы идентифицировать систему¹. Чтобы определить параметры системы необходимо, в первую очередь, оценить ее порядок.

Порядок динамической системы – это степень наибольшей из производных Y по отношению к t.

Динамическая система первого порядка

Рассмотрим входной и выходной сигналы, типичные для системы первого порядка (рис. 7).

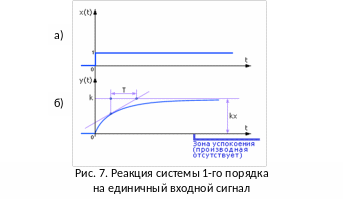
Пусть на вход системы, до того находившейся в покое, подали единичный сигнал 1[t] – единичная функция Хэвисайда (она изображена как зависимость x(t) на рис. 7а). Такой сигнал является одним из нескольких эталонных испытательных сигналов². Если на вход подается сигнал в виде функции Хэвисайда при нулевых начальных условиях, то реакция на выходе будет называться переходной функцией или переходной характеристикой h(t) (рис. 7б).

Ожидается, что система на выходе должна увеличить сигнал x в k раз и дойти до значения kx. Параметр k называют коэффициентом усиления входного сигнала.

Сигнал на выходе нарастает постепенно, инерционно. Переход от нуля до kx – процесс динамический, в сигнале присутствует изменение, которое описывается производной, и выход оказывается меньше входа на некоторую величину f: .

Если на выходе наблюдается экспоненциальный сигнал, то f выражается как , где параметр T – инерционность системы, является константой. Тогда система называется системой (или звеном) первого порядка, а ее поведение описывается уравнением с двумя параметрами T и k.

Чтобы определить, является ли кривая экспонентой, в каждой ее точке проводится касательная до пересечения с линией установившегося уровня (на рис. 7 это линия y(t)=k). Если кривая является экспонентой, то величина T в любой точке будет постоянной.

При определении модели требуется найти неизвестные коэффициенты k и T. Коэффициент k характеризует способность системы к усилению, а T – инерционность системы (память). Чем больше T, тем медленнее система реагирует на входной сигнал.