3. Динамическая регрессионная модель

Суть задания – коллективно разработать программу, определяющую динамическую регрессионную модель для звена 2 порядка¹.

Предполагается, что для проверки работы программы будет задан набор значений являющийся табличным представлением некоторой функции Y(t) – решения дифференциального уравнения 2 порядка

с заданными постоянными и . Для имитации экспериментальных результатов, к полученным значениям Y добавляется "погрешность измерений" – случайная добавка.

Вариант №1. Обеспечение тестового задания и разработка интерфейса общей программы (считывание данных и вывод результатов в числовом и графическом виде).

Вариант №2. Формирование матрицы и столбца свободных членов для динамической регрессионной модели 2 порядка со входным сигналов в виде функции Хэвисайда (см. уравнение (3) и обозначения (4)).

Вариант №3. Реализация метода Крамера решения систем линейных уравнений 3 порядка.

Вариант №4. Создание процедуры, реализующей аналитическое решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами и постоянной правой частью. Обратить внимание, что решения различны в зависимости от значений коэффициентов уравнения (см. приложение 1).

Вариант №5. Построение имитации поведения системы по определенной ранее модели (т.е. с использованием найденных ранее коэффициентов).

4. Метод Монте-Карло и генераторы случайных чисел

А. Методом Монте-Карло определить

1) значение интеграла

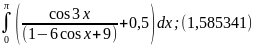
2) вероятность выпадения комбинации 5-6 на двух игральных костях;

3) вероятность вытащить из колоды (36 карт) подряд три карты одной масти;

4) вероятность выбросить тройку (три одинаковых камня) на пяти игральных костях;

5) значение интеграла

6) вероятность получить 2-х тузов при сдаче в преферансе (32 карты от 7 до туза, сдается по 10 карт).

Б. Параллельно с решением поставленной задачи проверить используемый ГСЧ на

• равномерность распределения (рассчитать, математическое ожидание, дисперсию, среднеквадратичное отклонение, провести частотный тест и проверку по критерию );

• статистическую независимость.

5. Моделирование смо

1. Необходимо выбрать некую систему массового обслуживания и создать ее модель, используя один из четырех основных принципов регламентации событий (принцип , принцип особых состояний, принцип последовательной проводки заявок или принцип параллельной работы объектов). Обосновать выбор принципа построения алгоритма.

2. Исследовать систему с помощью созданной модели, представить результаты в виде статистически обработанных данных. Сделать выводы о работе системы.

3. Рассмотреть, к каким результатам приведет изменение параметров системы.

4. Оценить точность статических характеристик.

Пример моделирования системы массового обслуживания с использованием принципа последовательной проводки заявок можно найти в приложении 4.

Приложения

Приложение 1. Справочная информация о решении линейных дифференциальных уравнений 2 порядка.

Решением неоднородного дифференциального уравнения является суперпозиция общего решения 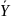однородного уравнения и частного решения 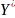неоднородного уравнения.

Если в правой части уравнения стоит многочлен k-й степени , то частное решение неоднородного уравнения можно искать в виде многочлена той же степени .

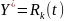Решение однородного уравнения

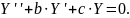
Характеристическое уравнение:

его решения – характеристические числа:

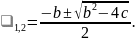
1. Если 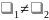, то

Если 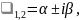то общее решение можно записать в форме

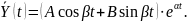
2. Если 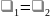, то

Приложение 2. Некоторые точки χ²-распределения

Таблица 1

Некоторые точки χ²-распределения

	0,99	0,95	0,75	0,50	0,25	0,05	0,01
1	0.00016	0.00393	0.1015	0.4549	1.323	3.841	6.635
2	0.02010	0.1026	0.5754	1.386	2.773	5.991	9.210
3	0.1148	0.3518	1.213	2.366	4.108	7.815	11.34
4	0.2971	0.7107	1.923	3.357	5.385	9.488	13.28
5	0.5543	1.1455	2.675	4.351	6.626	11.07	15.09
6	0.8721	1.635	3.455	5.348	7.841	12.59	16.81
7	1.239	2.167	4.255	6.346	9.037	14.07	18.48
8	1.646	2.733	5.071	7.344	10.22	15.51	20.09
9	2.088	3.325	5.899	8.343	11.39	16.92	21.67
10	2.558	3.940	6.737	9.342	12.55	18.31	23.21
15	5.229	7.261	11.04	14.34	18.25	25.00	30.58
20	8.260	10.85	15.45	19.34	23.83	31.41	37.57
30	14.95	18.49	24.48	29.34	34.80	43.77	50.89

Пример.

Пусть для получено экспериментально 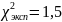. В строке таблицы 1, соответствующей 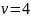, находим, что это значение соответствует (меньше указанного для , но больше указанного для предыдущего ). Следовательно, отклонение истинного распределения от идеального с вероятностью 0,75 обусловлено случайными причинами, а не тем, что наш генератор не способен генерировать равномерно распределенные случайные числа.

Приложение 3. Основные сведения о законах распределения случайных величин

Функцией распределения F(x) случайной величины X называется вероятность того, что случайная величина X примет значение, меньшее x: F(x) называют также интегральной функцией распределения или интегральным законом распределения (рис. 13).

Плотностью распределения или дифференциальной функцией распределения (рис. 13) называют функцию

Важные соотношения:

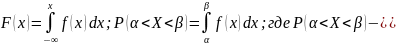
вероятность попадания величины X на отрезок

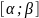
Свойства функций распределения:

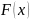– неубывающая функция;

Математическое ожидание для непрерывного распределения выражается как

и, соответственно, среднее квадратическое отклонение .
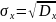